Sannolikhet
inlärningsmål
· definiera händelse, resultat, rättegång, enkel händelse, provutrymme och beräkna sannolikheten för att en händelse kommer att inträffa.
· beräkna sannolikheten för händelser för mer komplexa resultat.
· Lös program som involverar sannolikheter.
introduktion
Sannolikhet ger ett mått på hur troligt det är att något kommer att inträffa., Det är ett tal mellan och inklusive siffrorna 0 och 1. Det kan skrivas som en bråkdel, en decimal eller en procent.

att plocka siffror slumpmässigt innebär att det inte finns någon specifik ordning i vilken de väljs. Många spel använder tärningar eller spinnare för att generera siffror slumpmässigt. Om du förstår hur man beräknar sannolikheter kan du fatta tankeväckande beslut om hur man spelar dessa spel genom att veta sannolikheten för olika resultat.,
definitioner
först måste du veta några termer relaterade till Sannolikhet. När man arbetar med Sannolikhet kallas en slumpmässig åtgärd eller serie åtgärder en rättegång. Ett resultat är resultatet av en rättegång, och en händelse är en viss samling resultat. Händelser beskrivs vanligtvis med hjälp av en gemensam egenskap av resultaten.
låt oss tillämpa detta språk för att se hur termerna fungerar i praktiken. Vissa spel kräver rullande en munstycke med sex sidor, numrerade från 1 till 6. (Dice är plural av dö.,) Diagrammet nedan visar användningen av försök, resultat och händelse för ett sådant spel:
Observera att en samling resultat sätts i hängslen och separeras med kommatecken.
en enkel händelse är en händelse med endast ett resultat. Rullande en 1 skulle vara en enkel händelse, eftersom det bara finns ett resultat som fungerar-1! Rullande mer än en 5 skulle också vara en enkel händelse, eftersom händelsen innehåller endast 6 som ett giltigt resultat. En sammansatt händelse är en händelse med mer än ett resultat. Till exempel, i rullande en sexsidig dö, rullande ett jämnt tal kan uppstå med ett av tre resultat: 2, 4 och 6.,
När du rullar en sexsidig dö många gånger, bör du inte förvänta dig något resultat att hända oftare än en annan (förutsatt att det är en rättvis dö). Resultaten i en situation som denna sägs vara lika sannolika. Det är mycket viktigt att känna igen när resultaten är lika sannolikt vid beräkning Sannolikhet. Eftersom varje resultat i den rullande provningen är lika troligt, förväntar du dig att få varje resultat ![]() av rullarna., Det innebär att du förväntar dig att
av rullarna., Det innebär att du förväntar dig att![]() av rullarna ska vara 1,
av rullarna ska vara 1,![]() av rullarna ska vara 2,
av rullarna ska vara 2,![]() av rullarna ska vara 3 och så vidare.
av rullarna ska vara 3 och så vidare.
en spinner är uppdelad i fyra lika delar, var och en färgad med en annan färg som visas nedan. När spinnaren snurras pekar pilen på en av färgerna. Är resultaten lika troliga?
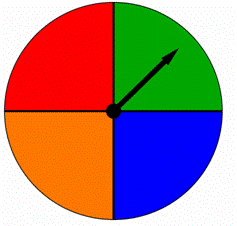
a) ja, de är lika troliga.
b) nej, de är inte lika troliga.,
Sannolikhet för händelser
sannolikheten för en händelse är hur ofta den förväntas inträffa. Det är förhållandet mellan händelsens storlek och storleken på provutrymmet.
först måste du bestämma storleken på provutrymmet. Storleken på provutrymmet är det totala antalet möjliga resultat. Till exempel, när du rullar 1 dör, är provutrymmet 1, 2, 3, 4, 5, 6. Så storleken på provutrymmet är 6.
då måste du bestämma storleken på händelseutrymmet., Evenemangsytan är antalet resultat i den händelse du är intresserad av. Händelseutrymmet för att rulla ett nummer mindre än tre är 1 eller 2. Så storleken på händelseutrymmet är 2.
för lika sannolika resultat kan sannolikheten för en händelse e skrivas P(e).
![]()
|
exempel |
||
|
problem |
ett spel kräver att man rullar en sexsidig dö numrerad från 1 till 6., Vad är sannolikheten för att rulla ett jämnt nummer? |
|
|
provutrymme = {1, 2, 3, 4, 5, 6}
Händelseutrymme = {2, 4, 6} |
hitta först sample space och event space. Provutrymmet är alla möjliga resultat, och händelseutrymmet är resultatet i evenemanget. I det här fallet rullar händelsen ett jämnt nummer.,” |
|
|
|
eftersom resultaten är lika troliga är sannolikheten för händelsen förhållandet mellan händelseutrymme och provutrymme., |
|
|
svar |
P(jämnt nummer) = |
iv id=” |
det är en vanlig praxis med sannolikheter, som med fraktioner i allmänhet, för att förenkla en Sannolikhet i lägsta termer eftersom det gör det lättare för de flesta att få en känsla av hur bra Det är. Om det inte finns anledning att inte göra det, uttrycka alla slutliga sannolikheter i lägsta termer.,
en spinner är uppdelad i lika delar, varje färgad med en annan färg som visas nedan., Hitta sannolikheten för att spinna blått eller grönt på den här spinnaren:
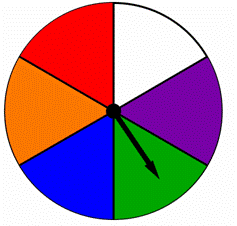
a) ![]()
b) ![]()
c) 2
d) 6
räkna metoder för att hitta provrum
det svåraste för att beräkna en sannolikhet kan vara att hitta storleken på provutrymmet, särskilt om det finns två eller flera försök. Det finns flera räkningsmetoder som kan hjälpa till.,
den första att titta på är att göra ett diagram. I exemplet nedan vänder Tori två mynt. Så du måste bestämma provutrymmet noggrant. Ett diagram som det som visas i exemplet som följer är ett bra tillvägagångssätt.
|
exempel |
||||
|
Problem |
Tori vänder ett par mynt och noterar hur många flips av ”huvuden” hon får. Vad är sannolikheten att hon vänder 2 huvuden?, Vad är sannolikheten att hon vänder bara 1 huvud?,15ecf6″>T |
T |
TT |
|
sample space: {HH, HT, TH, TT}
event space for 2 heads: {HH}
event space for 1 head: {HT, TH}
Create a chart to record the results of flipping the first coin, followed by the result of flipping the second coin.,
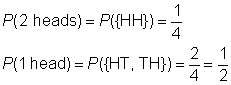
eftersom resultaten är lika troliga är sannolikheten för händelsen förhållandet mellan händelseutrymme och provutrymme.,
svara
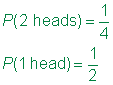
i exemplet nedan är provutrymmet för Tori enkelt eftersom endast ett munstycke rullas. Men eftersom James rullar två dör, hjälper ett diagram att organisera informationen.,
|
exempel |
||||||||
|
Problem |
Tori rullade en sexsidig dö och ville få ett resultat av antingen 1 eller 4. James rullade två sexsidiga tärningar, en blå och en röd, och ville få ett resultat av både en 1 och en 3, samtidigt. Vilken händelse har större sannolikhet?, |
|||||||
|
Tori’s sample space: {1, 2, 3, 4, 5, 6}
Tori’s event space: {1, 4}
Tori:
|
First, find the sample space and the event space for the two trials., För Toris rättegång är det enkelt. eftersom resultaten är lika troliga är sannolikheten för händelsen förhållandet mellan händelseutrymme och provutrymme.,316594724″> 6 |
6,1 |
6,2 |
6,3 |
6,4 |
6,5 |
6,6 |
|
James’ sample space has 36 outcomes.,
James’ händelseutrymme har 2 resultat.
det är inte så uppenbart för James rättegång, eftersom han rullar två tärningar. Använd ett diagram för att hitta möjligheterna.
det finns 36 resultat. Av dessa finns det 2 som har både 1 och 3.,
James: ![]()
eftersom resultaten är lika troliga är sannolikheten för händelsen förhållandet mellan händelseutrymme och provutrymme.
svar
Toris händelse har större sannolikhet.,
Du kan också använda ett träddiagram för att bestämma provutrymmet. Ett träddiagram har en gren för alla möjliga resultat för varje händelse.
Antag att en garderob har tre par byxor (svart, vit och grön), fyra skjortor (grön, vit, lila och gul) och två par skor (svart och vitt). Hur många olika outfits kan göras? Det finns 3 val för byxor, 4 val för skjortor och 2 val för skor., För vårt träddiagram, låt oss använda B för svart, W för vit, G för grön, P för lila och Y för gul.
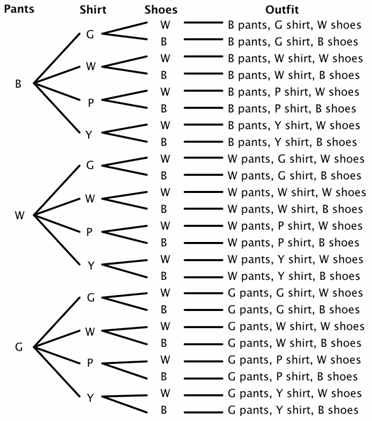
Du kan se från träddiagrammet att det finns 24 möjliga outfits (några kanske inte bra val) i provutrymmet.
Nu kan du ganska enkelt lösa vissa sannolikhetsproblem. Till exempel, Vad är sannolikheten att om du stänger dina ögon och väljer slumpmässigt skulle du välja byxor och skor med samma färg? Du kan se att det finns 8 kläder där byxorna och skorna matchar.,
![]()
som du har sett, när en rättegång involverar mer än ett slumpmässigt element, som att vända mer än ett mynt eller rulla mer än ett munstycke, behöver du inte alltid identifiera varje resultat i provutrymmet för att beräkna en sannolikhet. Du behöver bara antalet resultat.
den grundläggande Räkningsprincipen är ett sätt att hitta antalet resultat utan att lista och räkna var och en av dem.,
den grundläggande Räkningsprincipen
om en händelse har p möjliga resultat, och en annan händelse har m möjliga resultat, så finns det totalt p • m möjliga resultat för de två händelserna.
exempel
· rullande två sexsidiga tärningar: varje tärning har 6 lika sannolika resultat, så provutrymmet är 6 • 6 eller 36 lika sannolika resultat.
· vända tre mynt: varje mynt har 2 lika sannolika resultat, så provutrymmet är 2 • 2 • 2 eller 8 lika sannolika resultat.,
· rulla en sexsidig form och vända ett mynt: provutrymmet är 6 • 2 eller 12 lika sannolika resultat.
så du kan använda den grundläggande Räkningsprincipen för att ta reda på hur många outfits det finns i föregående exempel. Det finns 3 val för byxor, 4 val för skjortor och 2 val för skor. Med hjälp av den grundläggande Räkningsprincipen har du 4 • 3 • 2 = 24 olika outfits.,
|
exempel |
||
|
Problem |
Barry volontärer på en välgörenhetsresa för att göra luncher för alla andra volontärer. I varje påse sätter han: * en av två smörgåsar (jordnötssmör och gelé, eller kalkon och ost), · en av tre chips (vanliga potatischips, bakade potatischips eller majschips), · en bit frukt (ett äpple eller en apelsin)., han glömde att markera vad som fanns i påsarna. Förutsatt att varje val är lika troligt, vad är sannolikheten att påsen Therese får håller en jordnötssmör och gelé smörgås och ett äpple?, |
|
|
Size of sample space:
(number of sandwich choices) • (number of chip choices) • (number of fruit choices) = 2 • 3 • 2 = 12
|
First, use the Fundamental Counting Principle to find the size of the sample space., |
|
|
storlek på händelseutrymme:
(antal smörgåsval i händelse) • (antal chip val i händelse) • (antal frukt val i händelse) = |
för händelseutrymmet, följ samma princip. I det här fallet finns det bara en smörgås och en bit frukt av intresse, men någon av de tre typerna av chips är acceptabla., |
|
|
svar |
|
använd förhållandet för att hitta sannolikheten. |
Carrie vänder fyra mynt och räknar antalet svansar. Det finns fyra sätt att få exakt en svans: HHHT, HHTH, HTHH, och THHH. Vad är sannolikheten att Carrie får exakt en svans?,
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Summary
Probability helps you understand random, unpredictable situations where multiple outcomes are possible., Det är ett mått på sannolikheten för en händelse, och det beror på förhållandet mellan händelse och möjliga resultat, om alla dessa resultat är lika troliga.