Public Key Encryption (Svenska)

Public Key Cryptography

Till skillnad från symmetrisk key cryptography, finner vi inte historisk användning av public key cryptography. Det är ett relativt nytt koncept.

symmetrisk kryptografi var väl lämpad för organisationer som regeringar, militär och stora finansiella företag var inblandade i den klassificerade kommunikationen.,

med spridningen av mer osäkra datornätverk under de senaste decennierna kände man ett verkligt behov av att använda kryptografi i större skala. Den symmetriska nyckeln visade sig vara icke-praktisk på grund av utmaningar som den mötte för nyckelhantering. Detta gav upphov till de offentliga nyckelkryptosystemen.

processen för kryptering och dekryptering visas i följande illustration −

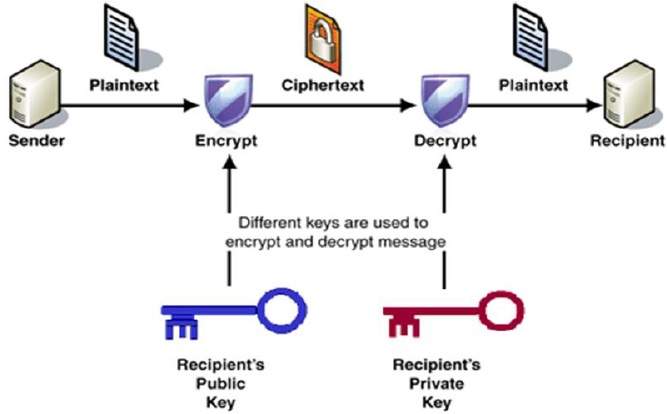
de viktigaste egenskaperna hos krypteringsschemat för offentlig nyckel är −

• olika nycklar används för kryptering och dekryptering., Detta är en egenskap som anger detta system annorlunda än symmetrisk krypteringsschema.

• varje mottagare har en unik dekrypteringsnyckel, vanligtvis kallad sin privata nyckel.

• mottagaren måste publicera en krypteringsnyckel, kallad hans offentliga nyckel.

• en viss försäkran om äktheten hos en offentlig nyckel behövs i detta system för att undvika spoofing av motståndare som mottagare. I allmänhet innebär denna typ av kryptosystem betrodd tredje part som intygar att en viss offentlig nyckel endast tillhör en viss person eller enhet.,

• krypteringsalgoritmen är komplex nog för att förhindra att angriparen drar av klartext från ciphertext och krypteringsnyckeln (public).

• även om privata och offentliga nycklar är matematiskt relaterade är det inte möjligt att beräkna den privata nyckeln från den offentliga nyckeln. Faktum är att intelligent del av något offentligt nyckelkryptosystem är att utforma ett förhållande mellan två nycklar.

det finns tre typer av krypteringssystem för offentlig nyckel., Vi diskuterar dem i följande avsnitt −

RSA Cryptosystem

det här kryptosystemet är ett det ursprungliga systemet. Det är fortfarande mest anställd cryptosystem även idag. Systemet uppfanns av tre forskare Ron Rivest, Adi Shamir och Len Adleman och därmed kallas det som RSA cryptosystem.

Vi kommer att se två aspekter av RSA-kryptosystemet, för det första generering av nyckelpar och för det andra krypteringsdekrypteringsalgoritmer.,

generering av RSA-nyckelpar

varje person eller en part som önskar delta i kommunikation med kryptering måste generera ett par nycklar, nämligen offentlig nyckel och privat nyckel. Processen som följs i generering av nycklar beskrivs nedan –

• generera RSA-modulen (n)

  • Välj två stora primtal, p och q.

  • beräkna n=p*q. för stark okrossbar kryptering, låt n vara ett stort antal, typiskt minst 512 bitar.,

• hitta härledda nummer (e)

  • antal e måste vara större än 1 och mindre än (P − 1)(q − 1).

  • det får inte finnas någon gemensam faktor för e och (P − 1)(q − 1) utom för 1. Med andra ord är två siffror e och (p – 1)(q – 1) coprime.

• Form the public key

  • paret av siffror (n, e) utgör RSA public key och offentliggörs.,

  • intressant, även om n är en del av den offentliga nyckeln, svårigheten att factorizing ett stort primtal säkerställer att angriparen inte kan hitta i begränsad tid de två primtal (p & q) används för att erhålla n. detta är styrkan i RSA.

• generera den privata nyckeln

  • privat nyckel d beräknas från p, q och e. för given n och e finns det unikt nummer d.

  • nummer d är inversen av e modulo (p – 1)(q – 1)., Detta innebär att d är numret mindre än(p – 1) (q – 1) så att när det multipliceras med e är det lika med 1 modulo(p – 1) (q – 1).

  • detta förhållande skrivs matematiskt enligt följande −

ed = 1 mod (p − 1)(q − 1)

den utökade euklidiska algoritmen tar p, q och e som ingång och ger d som utgång.

exempel

ett exempel på att generera RSA-nyckelpar ges nedan. (För att underlätta förståelsen är primes p & q som tas här små värden. Praktiskt taget är dessa värden mycket höga).,

• låt två primtal vara p = 7 och q = 13. Således modul n = pq = 7 x 13 = 91.

• välj E = 5, vilket är ett giltigt val eftersom det inte finns något nummer som är vanligt faktor 5 och(P-1) (q− 1) = 6 × 12 = 72, förutom 1.

• paret nummer (n, e) = (91, 5) utgör den offentliga nyckeln och kan göras tillgänglig för alla som vi vill kunna skicka oss krypterade meddelanden.

• Input p = 7, q = 13 och e = 5 till den utökade euklidiska algoritmen. Utgången kommer att vara d = 29.,

• kontrollera att d beräknas är korrekt genom att beräkna −

de = 29 × 5 = 145 = 1 mod 72

• därför är den offentliga nyckeln (91, 5) och privata nycklar (91, 29).

kryptering och dekryptering

När nyckelparet har genererats är processen för kryptering och dekryptering relativt enkel och beräkningsmässigt enkel.

intressant är att RSA inte fungerar direkt på strängar av bitar som vid symmetrisk nyckelkryptering. Det fungerar på siffror modulo n. därför är det nödvändigt att representera plaintext som en serie siffror mindre än n.,

RSA-kryptering

• Antag att avsändaren vill skicka ett textmeddelande till någon vars offentliga nyckel är (n, e).

• avsändaren representerar sedan plaintext som en serie av siffror mindre än n.

• för att kryptera den första plaintext P, vilket är ett tal modulo n. krypteringsprocessen är enkel matematisk steg som −

C = Pe mod n

• med andra ord är ciphertext C lika med den matematiska plaintext p multiplicerat med sig själv e gånger och sedan minskat modulo n. detta innebär att C är också ett tal mindre än n.,

• återgå till vår nyckel Generation exempel med plaintext P = 10, Vi får ciphertext c −

C = 105 mod 91

RSA dekryptering

• dekrypteringsprocessen för RSA är också mycket enkel. Antag att mottagaren av offentligt nyckelpar (n, e) har fått en ciphertext C.

• mottagaren höjer C till kraften i sin privata nyckel d. resultatet modulo n kommer att vara plaintext P.,

Plaintext = Cd mod n

• återvänder igen till vårt numeriska exempel, skulle ciphertext C = 82 få dekrypteras till nummer 10 med privat nyckel 29 −

Plaintext = 8229 mod 91 = 10

RSA-analys

säkerheten för RSA beror på styrkan hos två separata funktioner. RSA cryptosystem är mest populära offentliga nyckel kryptosystem styrka som bygger på den praktiska svårigheten att factoring det mycket stora antalet.,

• krypteringsfunktion − det anses vara en enkelriktad funktion för att konvertera plaintext till ciphertext och det kan endast vändas med kunskap om privat nyckel d.

• nyckelgenerering-svårigheten att bestämma en privat nyckel från en RSA − offentlig nyckel motsvarar faktoring av modul n. en angripare kan således inte använda kunskap om en RSA-offentlig nyckel för att bestämma en RSA-privat nyckel om han inte kan faktor n. det är också en enkelriktad funktion, som går från p& Q värden till modul n är lätt men omvänd är inte möjligt.,

om någon av dessa två funktioner bevisas icke envägs, kommer RSA att brytas. Faktum är att om en teknik för factoring effektivt utvecklas kommer RSA inte längre att vara säker.

styrkan i RSA-kryptering går drastiskt ner mot attacker om antalet p och q inte är stora primtal och / eller vald offentlig nyckel e är ett litet antal.

Elgamal Cryptosystem

tillsammans med RSA finns det andra krypto-system med öppen nyckel som föreslås. Många av dem är baserade på olika versioner av det diskreta Logaritmproblemet.,

Elgamal cryptosystem, som kallas elliptisk Kurvvariant, är baserat på det diskreta Logaritmproblemet. Det härleder styrkan från antagandet att de diskreta logaritmerna inte kan hittas i praktisk tidsram för ett visst nummer, medan den inversa driften av kraften kan beräknas effektivt.

Låt oss gå igenom en enkel version av ElGamal som fungerar med siffror modulo p. när det gäller elliptiska kurvvarianter är den baserad på ganska olika nummersystem.,

generering av Elgamal nyckelpar

varje användare av Elgamal cryptosystem genererar nyckelparet genom följande −

• välja en stor prime p. i allmänhet ett primtal av 1024 till 2048 bitar längd väljs.

• välja ett generatorelement g.

  • detta nummer måste vara mellan 1 och p − 1, men kan inte vara något nummer.

  • det är en generator av den multiplikativa gruppen av heltal modulo p. detta innebär för varje heltal M co-prime till p, det finns ett heltal k så att GK=a mod n.,

    till exempel är 3 generator av Grupp 5 (Z5 = {1, 2, 3, 4}).

n	3n	3N mod 5
1	3	3
2	9	4
3	27	2
4	81	1

• välja den privata nyckeln. Den privata nyckeln x är något nummer större än 1 och mindre än p-1.

• Computing del av den offentliga nyckeln., Värdet y beräknas från parametrarna p, g och den privata nyckeln x enligt följande −

y = gx mod p

• hämta offentlig nyckel. Elgamal public key består av de tre parametrarna (p, g, y).

  anta till exempel att p = 17 och att g = 6 (Det kan bekräftas att 6 är en generator av grupp Z17). Den privata nyckeln x kan vara något nummer större än 1 och mindre än 71, så vi väljer x = 5. Värdet y beräknas sedan enligt följande −

y = 65 mod 17 = 7

• den privata nyckeln är således 62 och den offentliga nyckeln är (17, 6, 7).,

kryptering och dekryptering

genereringen av ett Elgamal nyckelpar är jämförelsevis enklare än motsvarande process för RSA. Men kryptering och dekryptering är något mer komplexa än RSA.

Elgamal kryptering

Antag att avsändaren vill skicka en plaintext till någon vars Elgamal public key är (p, g, y), då −

• avsändaren representerar plaintext som en serie tal modulo p.

• för att kryptera den första plaintext P, som representeras som ett tal modulo p., Krypteringsprocessen för att erhålla ciphertext C är som följer −

  • genererar slumpmässigt ett nummer k;
  • beräkna två värden C1 och C2, där −

C1 = gk mod pC2 = (P*yk) mod p

• skicka ciphertext C, bestående av de två separata värdena (C1, C2), skickade tillsammans.,

• med hänvisning till vårt Elgamal key generation exempel ges ovan, plaintext P = 13 krypteras enligt följande −

  • slumpmässigt generera ett nummer, säger K = 10
  • beräkna de två värdena C1 och C2, där −

C1 = 610 mod 17C2 = (13*710) mod 17 = 9

• skicka ciphertext C = (C1, C2) = (15, 9).,

ElGamal dekryptering

• för att dekryptera ciphertext (C1, C2) med privat nyckel x, tas följande två steg −

  • beräkna den modulära inversen av (C1)x modulo p, som är (C1)-x , allmänt kallad dekrypteringsfaktor.,

  • hämta plaintext genom att använda följande formel −

C2 × (C1)-x mod p = Plaintext

• i vårt exempel, för att dekryptera ciphertext C = (C1, C2) = (15, 9) med privat nyckel x = 5, dekrypteringsfaktorn är

iv id=(15, 9) med privat nyckel x = 5, dekrypteringsfaktorn är

15-5 mod 17 = 9

• Extract plaintext p = (9 × 9) mod 17 = 13.

Elgamal analys

i ElGamal systemet, varje användare har en privat nyckel x. och har tre komponenter i offentlig nyckel-prime modul p, generator g, och offentliga Y = GX mod p., Elgamals styrka är baserad på svårigheten med diskret logaritmproblem.

den säkra nyckelstorleken är i allmänhet> 1024 bitar. Idag används även 2048 bitar lång nyckel. På bearbetningshastigheten är Elgamal ganska långsam, den används huvudsakligen för nyckelautentiseringsprotokoll. På grund av högre bearbetningseffektivitet blir elliptiska Kurvvarianter av ElGamal alltmer populära.,

elliptisk Curve Cryptography (ECC)

elliptisk Curve Cryptography (ECC) är en term som används för att beskriva en svit av kryptografiska verktyg och protokoll vars säkerhet är baserad på särskilda versioner av diskreta logaritmproblem. Det använder inte siffror modulo p.

ECC är baserat på uppsättningar av tal som är associerade med matematiska objekt som kallas elliptiska kurvor. Det finns regler för att lägga till och beräkna multiplar av dessa nummer, precis som det finns för siffror modulo p.,

ECC innehåller varianter av många kryptografiska system som ursprungligen utformades för modulära nummer som ElGamal kryptering och digital Signaturalgoritm.

man tror att det diskreta logaritmproblemet är mycket svårare när det appliceras på punkter på en elliptisk kurva. Detta uppmanar att byta från siffror modulo p till punkter på en elliptisk kurva. Även en likvärdig säkerhetsnivå kan erhållas med kortare nycklar om vi använder elliptiska kurvbaserade varianter.,

de kortare tangenterna resulterar i två fördelar −

• enkel nyckelhantering
• effektiv beräkning

dessa fördelar gör elliptiska kurvbaserade varianter av krypteringsschema mycket attraktiva för applikation där datorresurser är begränsade.

RSA-och Elgamalsystem-en jämförelse

låt oss kortfattat jämföra RSA-och Elgamalsystemen om de olika aspekterna.

RSA	ElGamal
det är effektivare för kryptering.	det är mer effektivt för dekryptering.,
det är mindre effektivt för dekryptering.	det är mer effektivt för dekryptering.
för en viss säkerhetsnivå krävs långa nycklar i RSA.	för samma säkerhetsnivå krävs mycket korta nycklar.
det är allmänt accepterat och används.	det är nytt och inte särskilt populärt på marknaden.