korrelationsforskning: söker relationer mellan variabler
i motsats till beskrivande forskning, som främst är utformad för att ge statiska bilder, innebär korrelationsforskning mätning av två eller flera relevanta variabler och en bedömning av förhållandet mellan eller bland dessa variabler., Variablerna för höjd och vikt är till exempel systematiskt relaterade (korrelerade) eftersom högre människor i allmänhet väger mer än kortare personer. På samma sätt är studietid och minnesfel också relaterade, eftersom ju mer tid en person ges för att studera en lista med ord, desto färre fel kommer han eller hon att göra. När det finns två variabler i forskningsdesignen kallas en av dem prediktorvariabeln och den andra resultatvariabeln., Forskningsdesignen kan visualiseras så här, där den krökta pilen representerar den förväntade korrelationen mellan de två variablerna:
figur 2.2.2

ett sätt att organisera data från en korrelationsstudie med två variabler är att gradera värdena för var och en av de uppmätta variablerna med hjälp av en scatter-plot. Som du kan se i Figur 2.10 ”exempel på Scatter-tomter” är en scatter-plot en visuell bild av förhållandet mellan två variabler., En punkt ritas för varje individ vid korsningen av hans eller hennes poäng för de två variablerna. När sambandet mellan variablerna på scatter-diagrammet lätt kan approximeras med en rak linje, som i delar (A) och (b) i Figur 2.10 ”exempel på Scatter-tomter”, sägs variablerna ha ett linjärt förhållande.
När den raka linjen indikerar att individer som har över medelvärden för en variabel också tenderar att ha över medelvärden för den andra variabeln, som i del (A), sägs förhållandet vara positivt linjärt., Exempel på positiva linjära relationer är de mellan höjd och vikt, mellan utbildning och inkomst och mellan ålder och matematiska förmågor hos barn. I varje fall tenderar personer som gör högre på en av variablerna också att göra högre poäng på den andra variabeln. Negativa linjära relationer, däremot, som visas i del b, inträffar när över-medelvärden för en variabel tenderar att associeras med under-medelvärden för den andra variabeln., Exempel på negativa linjära relationer är de mellan ett barns ålder och antalet blöjor som barnet använder, och mellan övning och fel som görs på en inlärningsuppgift. I dessa fall tenderar personer som gör högre poäng på en av variablerna att göra lägre poäng på den andra variabeln.
relationer mellan variabler som inte kan beskrivas med en rak linje kallas olinjära relationer. Del c i Figur 2.10 ”exempel på Scatter-tomter” visar ett gemensamt mönster där fördelningen av punkterna är väsentligen slumpmässig., I det här fallet finns det inget samband alls mellan de två variablerna, och de sägs vara oberoende. Delar (D) och (e) i Figur 2.10 ”exempel på Scatter tomter” visar föreningsmönster där, även om det finns en förening, punkterna inte är väl beskrivna av en enda rak linje. Till exempel, Del (d) visar vilken typ av relation som ofta uppstår mellan ångest och prestanda., Ökad ångest från låga till måttliga nivåer är förknippade med prestandaökningar, medan ökad ångest från måttliga till höga nivåer är förknippade med minskad prestanda. Relationer som förändras i riktning och därmed inte beskrivs av en enda rak linje kallas krökta relationer.
figur 2.10 exempel på Scatter tomter
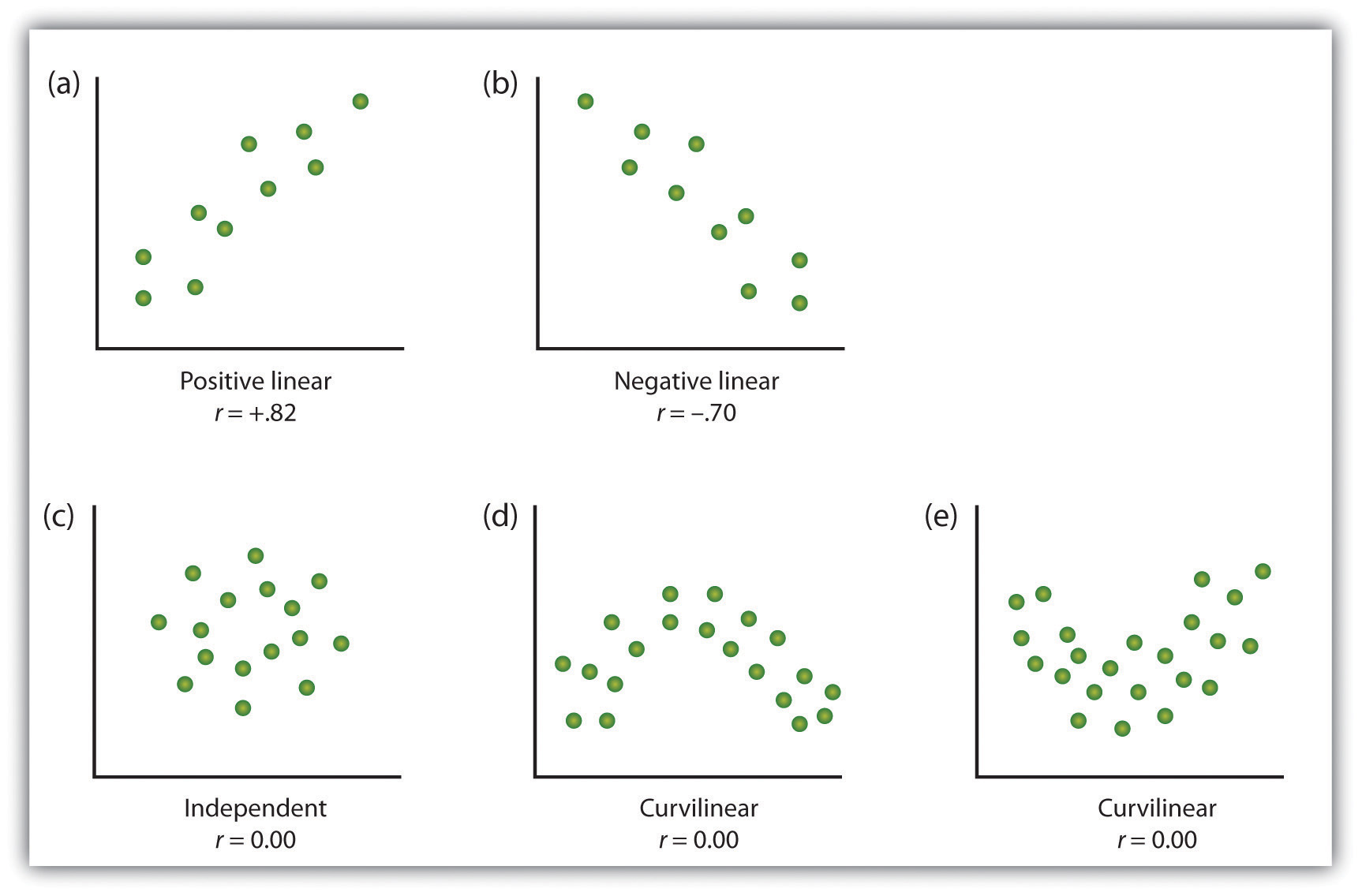
några exempel på relationer mellan två variabler som visas i scatter tomter., Observera att Pearson-korrelationskoefficienten (r) mellan variabler som har krökta relationer sannolikt kommer att ligga nära noll.
anpassad från Stangor, C. (2011). Forskningsmetoder för beteendevetenskap (4: e ed.). Bergsutsikt, CA: Cengage.
den vanligaste statistiska mätningen av styrkan hos linjära relationer mellan variabler är Pearson korrelationskoefficienten, som symboliseras av bokstaven r. värdet av korrelationskoefficienten varierar från r = -1.00 till r = + 1.00., Riktningen för det linjära förhållandet indikeras av tecknet på korrelationskoefficienten. Positiva värden för r (t .ex. r=.54 eller r = .67) indikerar att förhållandet är positivt linjärt (dvs mönstret av prickarna på scatter-tomten går från nedre vänstra till övre högra), medan negativa värden för r (t.ex. r=–.30 eller r = –.72) ange negativa linjära relationer(dvs prickarna går från övre vänstra till nedre högra). Styrkan hos det linjära förhållandet indexeras av korrelationskoefficientens avstånd från noll (dess absoluta värde)., Till exempel, r = –.54 är ett starkare förhållande än r = .30, och r = .72 är ett starkare förhållande än r = –.57. Eftersom Pearson-korrelationskoefficienten endast mäter linjära relationer, beskrivs variabler som har krökta relationer inte väl av r, och den observerade korrelationen kommer att ligga nära noll.
det är också möjligt att studera relationer mellan mer än två åtgärder samtidigt., En forskningsdesign där mer än en prediktorvariabel används för att förutsäga en enda resultatvariabel analyseras genom multipel regression (Aiken & West, 1991). Multiple regression är en statistisk teknik, baserad på korrelationskoefficienter bland variabler, som gör det möjligt att förutsäga ett enda utfall variabel från mer än en prediktor variabel. Till exempel, figur 2.11 ”förutsägelse av jobbprestanda från tre prediktorvariabler” visar en multipel regressionsanalys där tre prediktorvariabler används för att förutsäga ett enda resultat., Användningen av flera regressionsanalys visar en viktig fördel med korrelationsforskningsdesigner – de kan användas för att göra förutsägelser om en persons sannolika poäng på en resultatvariabel (t.ex. arbetsprestanda) baserat på kunskap om andra variabler.
figur 2.11 förutsägelse av jobbprestanda från tre prediktorvariabler
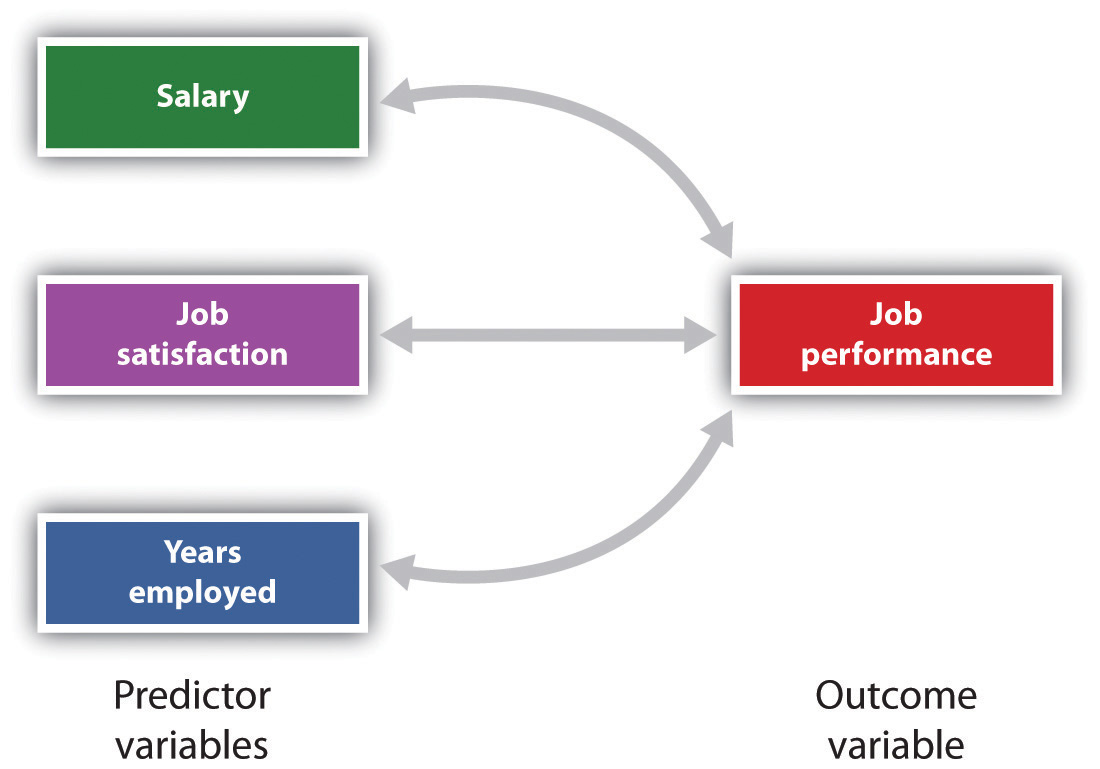
multipel regression gör det möjligt för forskare att förutsäga poängen på en enda resultatvariabel med mer än en prediktorvariabel.,
en viktig begränsning av korrelationsforskningsdesigner är att de inte kan användas för att dra slutsatser om orsakssambanden mellan de uppmätta variablerna. Tänk till exempel på en forskare som har hypoteser att visning av våldsamt beteende kommer att orsaka ökat aggressivt spel hos barn. Han har samlat, från ett urval av fjärde klass barn, ett mått på hur många våldsamma TV-program varje barn ser under veckan, samt ett mått på hur aggressivt varje barn spelar på skolgården., Från hans insamlade data upptäcker forskaren en positiv korrelation mellan de två uppmätta variablerna.
Även om denna positiva korrelation verkar stödja forskarens hypotes, kan det inte tas för att indikera att visning av våldsam TV orsakar aggressivt beteende. Även om forskaren är frestad att anta att visning av våldsam TV orsakar aggressivt spel,
figur 2.2.2

det finns andra möjligheter., En alternativ möjlighet är att orsaksriktningen är exakt motsatt från vad som har hypotesiserats. Kanske barn som har uppfört sig aggressivt i skolan utvecklar återstående spänning som leder dem till att vilja titta på våldsamma TV-program hemma:
figur 2.2.2

Även om denna möjlighet kan tyckas mindre sannolikt, finns det inget sätt att utesluta möjligheten till en sådan omvänd orsakssamband på grundval av denna observerade korrelation., Det är också möjligt att båda kausalriktningarna fungerar och att de två variablerna orsakar varandra:
figur 2.2.2

fortfarande en annan möjlig förklaring till den observerade korrelationen är att den har producerats genom närvaron av (även känd som en tredje variabel)., En gemensam orsaksvariabel är en variabel som inte ingår i forskningshypotesen men som orsakar både prediktorn och resultatvariabeln och därmed ger den observerade korrelationen mellan dem. I vårt exempel är en potentiell gemensam orsaksvariabel disciplinens stil hos barnens föräldrar. Föräldrar som använder en hård och bestraffande disciplin stil kan producera barn som både gillar att titta på våldsam TV och som beter sig aggressivt i jämförelse med barn vars föräldrar använder mindre hård disciplin:
figur 2.2.,2
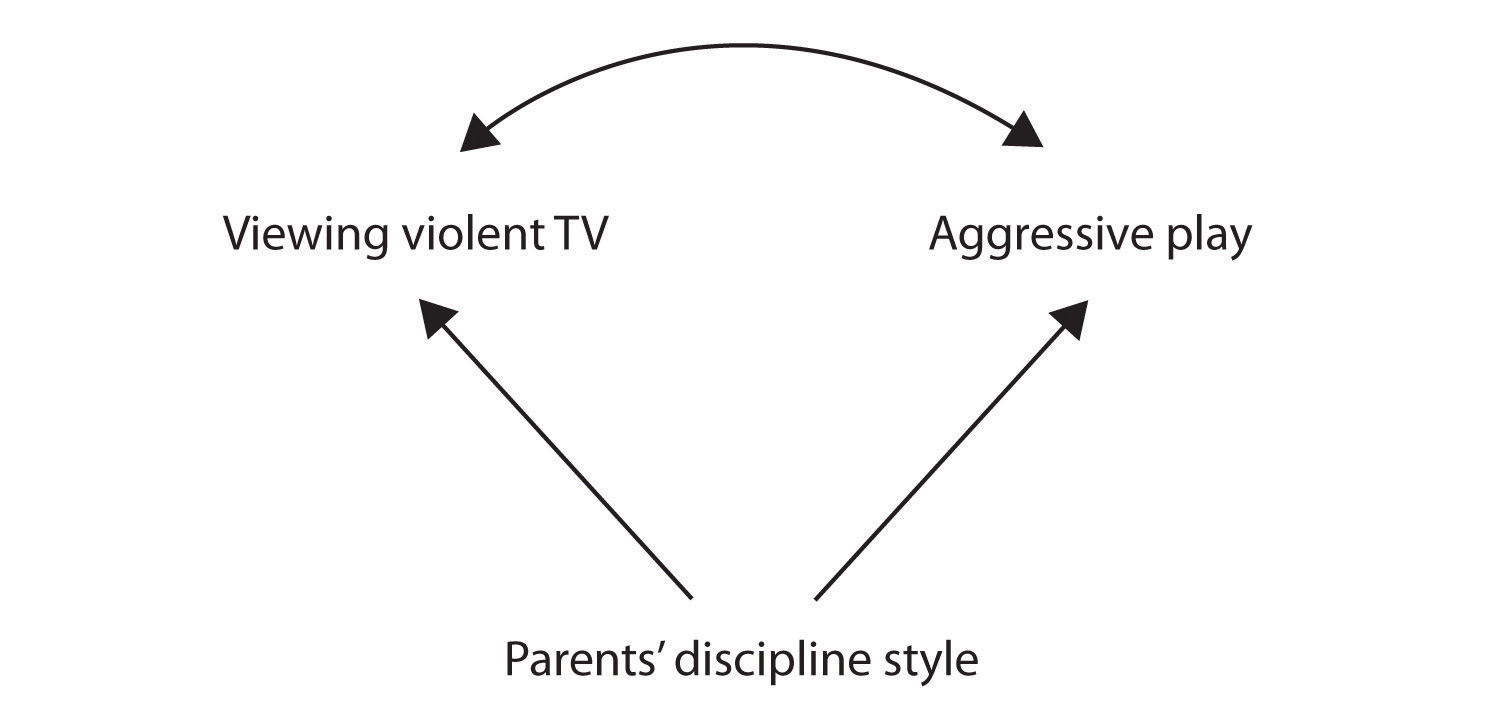
i det här fallet skulle tv-tittande och aggressivt spel vara positivt korrelerade (vilket indikeras av den krökta pilen mellan dem), även om ingen orsakade den andra men de orsakades båda av föräldrarnas disciplinstil (de raka pilarna). När prediktorn och utfallsvariablerna båda orsakas av en gemensam orsaksvariabel sägs det observerade förhållandet mellan dem vara falskt., Ett falskt förhållande är ett förhållande mellan två variabler där en gemensam orsaksvariabel producerar och ”förklarar bort” förhållandet. Om effekterna av den gemensamma orsaksvariabeln togs bort eller kontrollerades för, skulle förhållandet mellan prediktorn och utfallsvariablerna försvinna. I exemplet förhållandet mellan aggression och tv-tittande kan vara falska eftersom genom att kontrollera för effekten av föräldrarnas disciplinerande stil, förhållandet mellan tv-tittande och aggressivt beteende kan försvinna.,
vanliga orsaksvariabler i korrelationsforskningsdesigner kan ses som ”mysterium” – variabler eftersom deras närvaro och identitet vanligtvis är okända för forskaren, eftersom de inte har uppmätts. Eftersom det inte är möjligt att mäta varje variabel som kan orsaka både prediktorn och utfallsvariablerna är förekomsten av en okänd orsaksvariabel alltid en möjlighet. Av denna anledning är vi kvar med den grundläggande begränsningen av korrelationsforskning: korrelation visar inte orsakssamband., Det är viktigt att när du läser om korrelationsforskningsprojekt, du tänka på möjligheten av falska relationer, och se till att tolka resultaten på lämpligt sätt. Även om korrelationsforskning ibland rapporteras som att visa orsakssamband utan att nämna möjligheten till omvänd orsakssamband eller vanliga orsaksvariabler, är informerade konsumenter av forskning, som du, medvetna om dessa tolkningsproblem.
Sammanfattningsvis har korrelationsforskningsdesigner både styrkor och begränsningar., En styrka är att de kan användas när experimentell forskning inte är möjlig eftersom prediktorvariablerna inte kan manipuleras. Korrelationsmönster har också fördelen att låta forskaren studera beteende som det förekommer i vardagen. Och vi kan också använda korrelationsmönster för att göra förutsägelser—till exempel för att förutsäga från poängen på deras batteri av test framgången för arbetstränare under en träningspass. Men vi kan inte använda sådan korrelationsinformation för att avgöra om utbildningen orsakade bättre arbetsprestanda. För det är forskare beroende av experiment.,