Probability
Learning Objective(s)
· Define event, outcome, trial, simple event, sample space and calculate the probability that an event will occur.
· Calcule a probabilidade de eventos para resultados mais complexos.
· resolver aplicações envolvendo probabilidades.
Introdução
Probabilidade fornece uma medida de quão provável é que algo irá ocorrer., É um número entre e incluindo os números 0 e 1. Pode ser escrito como uma fração, um decimal, ou um por cento.

escolher números aleatoriamente significa que não há uma ordem específica em que eles são escolhidos. Muitos jogos usam dados ou spinners para gerar números aleatoriamente. Se você entender como calcular probabilidades, você pode tomar decisões pensativas sobre como jogar esses jogos, sabendo a probabilidade de vários resultados.,
Definições
Primeiro você precisa saber alguns termos relacionados com a probabilidade. Quando se trabalha com probabilidade,uma ação aleatória ou Série de ações é chamada de teste. Um resultado é o resultado de um julgamento, e um evento é uma coleção particular de resultados. Os eventos são geralmente descritos usando uma característica comum dos resultados.vamos aplicar esta linguagem para ver como os Termos funcionam na prática. Alguns jogos requerem gravar um dado com seis lados, numerados de 1 a 6. (Dado é o plural de morrer.,) O gráfico abaixo ilustra o uso de Teste, Resultado e evento para tal jogo:
Notice that a collection of outcomes is put in braces and separated by vírgulas.um evento simples é um evento com apenas um resultado. Rolar um 1 seria um evento simples, porque há apenas um resultado que funciona-1! Rolar mais de um 5 também seria um evento simples, porque o evento inclui apenas 6 como um resultado válido. Um evento composto é um evento com mais de um resultado. Por exemplo, ao rolar um dado de seis lados, rolar um número par pode ocorrer com um de três resultados: 2, 4 e 6.,
Quando você rola um dado de seis lados muitas vezes, você não deve esperar que qualquer resultado aconteça mais frequentemente do que outro (assumindo que é um dado justo). Os resultados em uma situação como esta são ditos ser igualmente prováveis. É muito importante reconhecer quando os resultados são igualmente prováveis ao calcular a probabilidade. Uma vez que cada resultado no ensaio de laminagem é igualmente provável, você esperaria obter cada resultado ![]() dos rolos., Isto é, você esperaria
dos rolos., Isto é, você esperaria ![]() dos rolos de 1,
dos rolos de 1, ![]() dos rolos 2,
dos rolos 2, ![]() dos rolos de 3, e assim por diante.
dos rolos de 3, e assim por diante.
um spinner é dividido em quatro partes iguais, cada uma colorida com uma cor diferente como mostrado abaixo. Quando este spinner é girado, a seta aponta para uma das cores. Os resultados são igualmente prováveis?
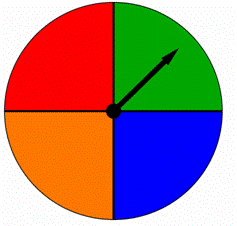
A) Sim, são igualmente prováveis.não, não são igualmente prováveis.,
Probability of Events
a probabilidade de um evento é a frequência com que se espera que ocorra. É a razão entre o tamanho do espaço do evento e o tamanho do espaço da amostra.
primeiro, você precisa determinar o tamanho do espaço de amostra. O tamanho do espaço de amostra é o número total de resultados possíveis. Por exemplo, quando você rola 1 morrer, o espaço de amostra é 1, 2, 3, 4, 5, 6. Então o tamanho do espaço de amostra é 6.
então você precisa determinar o tamanho do espaço do evento., O espaço do evento é o número de resultados no evento que você está interessado. O espaço de evento para rodar um número inferior a três é 1 ou 2. Então o tamanho do espaço do evento é 2.
para resultados igualmente prováveis, a probabilidade de um evento e pode ser escrita P(e).
![]()
|
Exemplo |
||
|
Problema |
Um jogo requer rolando um de seis lados morrer, numerados de 1 a 6., Qual é a probabilidade de rolar um número par? |
|
|
Exemplo de espaço = {1, 2, 3, 4, 5, 6}
espaço para Eventos = {2, 4, 6} |
Primeiro, encontrar o exemplo do espaço e o espaço do evento. O espaço de amostra é todos os resultados possíveis, e o espaço de Evento são os resultados no evento. Neste caso, o evento está ” rodando um número par.,” |
|
|
|
, Pois os resultados são igualmente prováveis, a probabilidade de o evento é a relação de espaço para eventos a exemplo de espaço., |
|
|
Resposta |
P(número par) = |
|
é uma prática comum com probabilidades, como com frações em geral, para simplificar uma probabilidade em termos mais baixos desde que torna mais fácil para a maioria das pessoas para se ter uma noção de quão grande ele é. A menos que haja razão para não o fazer, expresse todas as probabilidades finais em termos mais baixos.,
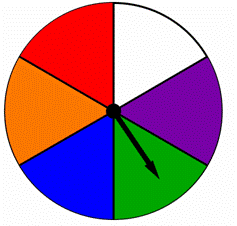
um spinner é dividido em partes iguais, cada uma colorida com uma cor diferente como mostrado abaixo., Encontrar a probabilidade de fiação azul ou verde neste botão rotativo:
A) ![]()
B) ![]()
C) 2
D) 6
Métodos de Contagem para encontrar Exemplo de Espaços
A coisa mais difícil para o cálculo de uma probabilidade pode ser encontrar o tamanho da amostra espaço, especialmente se houver dois ou mais ensaios. Existem vários métodos de contagem que podem ajudar.,
O primeiro a olhar é fazendo um gráfico. No exemplo abaixo, Tori está flipando duas moedas. Então você precisa determinar o espaço da amostra com cuidado. Um gráfico como o mostrado no exemplo que se segue é uma boa abordagem.
|
Exemplo |
||||
|
Problema |
Tori está lançando um par de moedas e observar como muitos lançamentos de “cabeças” que ela recebe. Qual é a probabilidade de ela virar duas cabeças?, Qual é a probabilidade de ela virar apenas uma cabeça?,15ecf6″>T |
T |
TT |
|
sample space: {HH, HT, TH, TT}
event space for 2 heads: {HH}
event space for 1 head: {HT, TH}
Create a chart to record the results of flipping the first coin, followed by the result of flipping the second coin.,
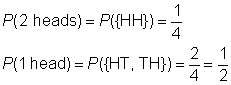
, Pois os resultados são igualmente prováveis, a probabilidade de o evento é a relação de espaço para eventos a exemplo de espaço.,
Resposta
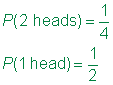
No exemplo abaixo, o exemplo de espaço para Tori é simples como apenas um dado é rolado. No entanto, uma vez que James está rodando dois die, um gráfico ajuda a organizar a informação.,
|
Exemplo |
||||||||
|
Problema |
Tori rolou um de seis lados morrer e queria obter um resultado de 1 ou 4. James rolou dois dados de seis lados, um azul e um vermelho, e queria obter um resultado de um 1 e um 3, ao mesmo tempo. Qual evento tem uma probabilidade maior?, |
|||||||
|
Tori’s sample space: {1, 2, 3, 4, 5, 6}
Tori’s event space: {1, 4}
Tori:
|
First, find the sample space and the event space for the two trials., Para o julgamento da Tori, isto é simples. Uma vez que os resultados são igualmente prováveis, a probabilidade do evento é a razão de espaço de evento para espaço de amostra.,316594724″> 6 |
6,1 |
6,2 |
6,3 |
6,4 |
6,5 |
6,6 |
|
James’ sample space has 36 outcomes.,
James ‘ event space has 2 outcomes.
não é tão óbvio para o julgamento de James, uma vez que ele está lançando dois dados. Use um gráfico para encontrar as possibilidades.existem 36 resultados. Destes, há dois que têm tanto 1 quanto 3.,
James: ![]()
, Pois os resultados são igualmente prováveis, a probabilidade de o evento é a relação de espaço para eventos a exemplo de espaço.
Resposta
Tori evento tem uma maior probabilidade.,
Pode também utilizar um diagrama em árvore para determinar o espaço da amostra. Um diagrama de árvore tem um ramo para cada resultado possível para cada evento.suponha que um armário tenha três pares de calças (preto, branco e verde), quatro camisas (verde, branco, roxo e amarelo), e dois pares de sapatos (preto e branco). Quantas roupas diferentes podem ser feitas? Há 3 escolhas para Calças, 4 escolhas para camisas, e 2 escolhas para sapatos., Para nosso diagrama de árvore, vamos usar B para preto, W para branco, G para verde, P para roxo, e Y para amarelo.
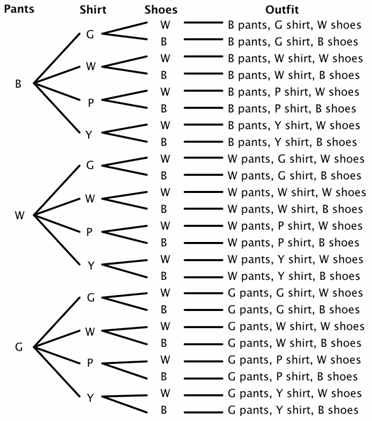
Você pode ver no diagrama da árvore que existem 24 vestimentas possíveis (algumas talvez não grandes escolhas) no espaço de amostra.
Agora você poderia razoavelmente facilmente resolver alguns problemas de probabilidade. Por exemplo, Qual é a probabilidade de que se você fechar os olhos e escolher aleatoriamente você escolheria calças e sapatos com a mesma cor? Você pode ver que há oito roupas onde as calças e os sapatos combinam.,
![]()
Como já foi visto, quando um julgamento envolve mais do que um elemento aleatório, tais como inversão de mais de uma moeda ou de material mais do que um dado, não é sempre necessário identificar cada resultado no exemplo de espaço para calcular uma probabilidade. Você só precisa do número de resultados.
O princípio Fundamental da contagem é uma maneira de encontrar o número de resultados sem listar e contar cada um deles.,
The Fundamental Counting Principle
If one event has p possible outcomes, and another event has m possible outcomes, then there are a total of p • m possible outcomes for the two events.
exemplos
· lançamento de dois dados de seis lados: cada dado tem 6 resultados igualmente prováveis, de modo que o espaço de amostra é 6 • 6 ou 36 resultados igualmente prováveis.
* Flipping three coins: Each coin has 2 equally likely outcomes, so the sample space is 2 • 2 • 2 ou 8 resultados igualmente prováveis.,
· rolar um dado de seis lados e virar uma moeda: o espaço de amostragem é 6 • 2 ou 12 resultados igualmente prováveis.
assim você poderia usar o princípio Fundamental de contagem para descobrir quantas roupas existem no exemplo anterior. Há 3 escolhas para Calças, 4 escolhas para camisas, e 2 escolhas para sapatos. Usando o princípio Fundamental de Contagem, você tem 4 • 3 • 2 = 24 roupas diferentes.,
|
Exemplo |
||
|
Problema |
Barry voluntários em uma instituição de caridade a pé para fazer almoços para todos os outros voluntários. Em cada saco, ele coloca: · um dos dois sanduíches de manteiga de amendoim e geléia, ou da turquia, e queijo), · um dos três chips (regular batata frita, batata assada batata frita ou chips de milho), · uma peça de fruta (maçã ou uma laranja).,esqueceu-se de marcar o que estava nos sacos. Assumindo que cada escolha é igualmente provável, Qual é a probabilidade que o saco que a Therese recebe contém uma sandes de manteiga de amendoim e geleia e uma maçã?, |
|
|
Size of sample space:
(number of sandwich choices) • (number of chip choices) • (number of fruit choices) = 2 • 3 • 2 = 12
|
First, use the Fundamental Counting Principle to find the size of the sample space., |
|
|
Tamanho de espaço para eventos:
(número de sanduíche de escolhas no evento) • (número do chip escolhas no evento) • (número de frutos de escolhas no evento) = |
o espaço do evento, seguem o mesmo princípio. Neste caso, há apenas uma sanduíche e uma peça de fruta de interesse, mas qualquer um dos três tipos de chips são aceitáveis., |
|
|
Resposta |
|
Usar a relação para encontrar a probabilidade. |
Carrie vira quatro moedas e conta o número de caudas. Há quatro maneiras de conseguir exatamente uma cauda: HHHT, HHTH, HTHH, e THHH. Qual é a probabilidade de a Carrie receber exactamente uma cauda?,
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Summary
Probability helps you understand random, unpredictable situations where multiple outcomes are possible., É uma medida da probabilidade de um evento, e depende da relação de Evento e possíveis resultados, se todos esses resultados são igualmente prováveis.