Números imaginários (Português)

um número imaginário,ao quadrado, dá um resultado negativo.

Tente

Vamos tentar elevar alguns números para ver se podemos obter um resultado negativo:

Sem sorte! Sempre positivo, ou zero.

parece que não podemos multiplicar um número por si só para obter uma resposta negativa …,

… mas imagine que existe tal número (chame-o de I para imaginário) que poderia fazer isso: i × i = -1 seria útil, e o que poderíamos fazer com ele?

Bem, tomando a raiz quadrada de ambos os lados obtemos isto:

o que significa que o eu é a resposta para a raiz quadrada de-1.

Que é realmente muito útil porque …

vamos ter um go:

Ei! isso foi interessante! A raiz quadrada de -9 é simplesmente a raiz quadrada de + 9, vezes I.,

Em geral:

desde que mantenhamos o pequeno “eu” lá para nos lembrar que nós ainda
preciso multiplicar por √-1 estamos seguro para continuar com a nossa solução!

usando i

Interessante! Usamos um número imaginário (5i) e acabamos com uma solução real (-25).,

os números Imaginários podem ajudar-nos a resolver algumas equações:

Unidade Imaginária Número

A raiz quadrada de menos um √(-1) é a “unidade” Número Imaginário, o equivalente a 1 para Números Reais.

em matemática, o símbolo para √(-1) é i para imaginário.pode ficar com a raiz quadrada de -1?Bem, eu posso!

But in electronics they use j (because “i” already means current, and the next letter after i is j).,

Examples of Imaginary Numbers

Imaginary Numbers are not “Imaginary”

Imaginary Numbers were once thought to be impossible, and so they were called “Imaginary” (to make fun of them).,

mas então as pessoas pesquisaram mais e descobriram que eram realmente úteis e importantes porque preenchiam uma lacuna na matemática … mas o nome” imaginário ” ficou preso.

E foi assim que surgiu o nome “números reais” (real não é imaginário).,

os Números Imaginários são Úteis

Números Complexos

os números Imaginários tornar-se mais útil quando combinado com números reais para fazer os números complexos como 3+5i ou 6−4i

Analisador de espectro

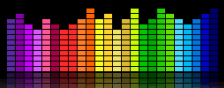
Que legal mostra que você vê quando a música está tocando? Sim, números complexos são usados para calculá-los! Usando algo chamado “transformação de Fourier”.,

na verdade, muitas coisas inteligentes podem ser feitas com som usando números complexos, como filtrar sons, ouvir sussurros em uma multidão e assim por diante.

é parte de um assunto chamado “processamento de sinal”.

Eletricidade

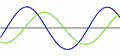
CA (Corrente Alternada) de Eletricidade alterações entre o positivo e o negativo de uma onda senoidal.

quando combinamos duas correntes AC elas podem não corresponder corretamente, e pode ser muito difícil descobrir a nova corrente.,

mas usando números complexos torna muito mais fácil fazer os cálculos.

E o resultado pode ter corrente “imaginária”, mas ainda pode magoá-lo!

Mandelbrot Set

o belo conjunto de Mandelbrot (parte dele é ilustrada aqui) é baseado em números complexos.,

Equação Quadrática

A Equação Quadrática, que tem muitos usos,
pode dar os resultados que incluem números imaginários

Também a Ciência, a mecânica Quântica e a Relatividade usar números complexos.

propriedade interessante

o número imaginário da Unidade, I, tem uma propriedade interessante., It “cycles” through 4 different values each time we multiply:

1 × i = i i × i = −1 −1 × i = −i −i × i = 1 Back to 1 again!,

So we have this: