Correlational Pesquisa: em Busca de Relações Entre Variáveis
Em contraste com a investigação descritiva, que é projetado principalmente para fornecer imagens estáticas, correlational pesquisa envolve a medição de duas ou mais variáveis relevantes e a avaliação da relação entre essas variáveis., Por exemplo, as variáveis de altura e peso são sistematicamente relacionadas (correlacionadas) porque pessoas mais altas geralmente pesam mais do que pessoas mais curtas. Da mesma forma, Tempo de estudo e erros de memória também estão relacionados, porque quanto mais tempo uma pessoa é dada para estudar uma lista de palavras, menos erros ele ou ela vai fazer. Quando existem duas variáveis no projeto de pesquisa, uma delas é chamada de variável predictor e a outra a variável resultado., O projeto de pesquisa pode ser visualizado como este, onde a seta curva representa a esperada correlação entre as duas variáveis:
Figura 2.2.2

Uma forma de organizar os dados a partir de um correlational estudo com duas variáveis é de gráfico os valores de cada uma das grandezas de medida usando um gráfico de dispersão. Como você pode ver na figura 2.10 “exemplos de parcelas de dispersão”, uma parcela de dispersão é uma imagem visual da relação entre duas variáveis., Um ponto é plotado para cada indivíduo na interseção de suas pontuações para as duas variáveis. Quando a associação entre as variáveis na parcela de dispersão pode ser facilmente aproximada com uma linha reta, como nas partes (a) e (b) da figura 2.10 “exemplos de parcelas de dispersão”, as variáveis são ditas ter uma relação linear.
Quando a linha reta indica que os indivíduos que têm valores acima da média para uma variável também tendem a ter valores acima da média para a outra variável, como na parte a), a relação é dita ser positiva linear., Exemplos de relações lineares positivas incluem aquelas entre altura e peso, entre educação e renda, e entre idade e habilidades matemáticas em crianças. Em cada caso, as pessoas que pontuam mais alto em uma das variáveis também tendem a pontuar mais alto na outra variável. Relações lineares negativas, em contraste, como mostrado na Parte b), ocorrem quando valores acima da média para uma variável tendem a ser associados com valores abaixo da média para a outra variável., Exemplos de relações lineares negativas incluem aquelas entre a idade de uma criança e o número de fraldas que a criança usa, e entre a prática e erros cometidos em uma tarefa de aprendizagem. Nestes casos, as pessoas que pontuam mais alto em uma das variáveis tendem a marcar mais baixo na outra variável.
As relações entre variáveis que não podem ser descritas com uma linha reta são conhecidas como relações não lineares. A parte c) da figura 2.10 “exemplos de parcelas de dispersão” mostra um padrão comum em que a distribuição dos pontos é essencialmente aleatória., Neste caso, não existe qualquer relação entre as duas variáveis, e dizem-se que elas são independentes. As partes (d) e (e) da figura 2.10 “exemplos de parcelas de dispersão” mostram padrões de associação em que, embora exista uma Associação, os pontos não são bem descritos por uma única linha reta. Por exemplo, Parte (d) mostra o tipo de relação que frequentemente ocorre entre ansiedade e desempenho., Aumentos na ansiedade de níveis baixos a moderados estão associados a aumentos de desempenho, enquanto aumentos na ansiedade de níveis moderados a elevados estão associados a diminuições no desempenho. Relações que mudam de direção e, portanto, não são descritas por uma única linha reta são chamadas relações curvilíneas.
Figura 2.10 Exemplos de gráficos de Dispersão
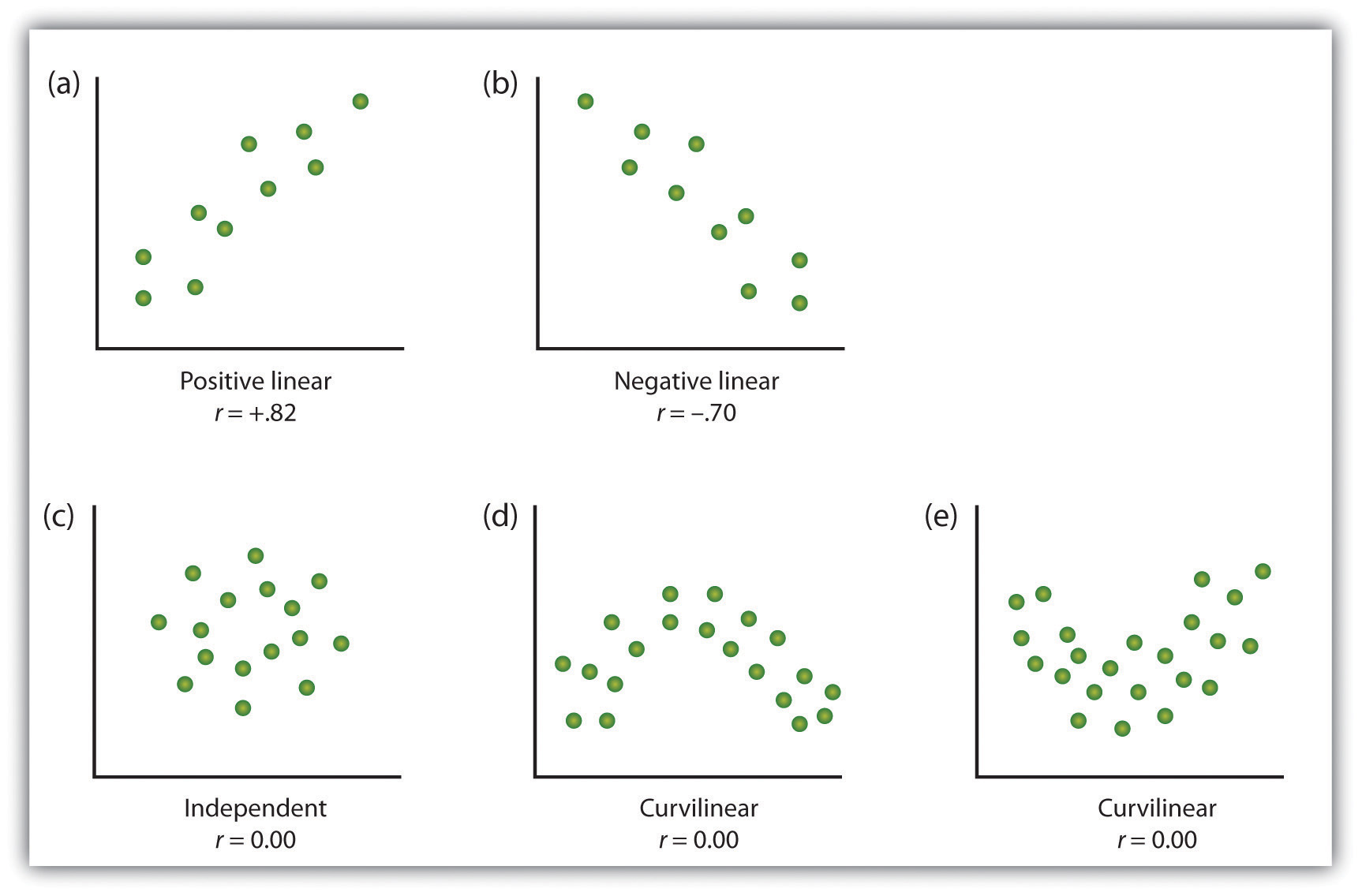
Alguns exemplos de relações entre duas variáveis, como mostrado em gráficos de dispersão., Note que o coeficiente de correlação de Pearson (r) entre variáveis que têm relações curvilíneas provavelmente será próximo de zero.
adaptado de Stangor, C. (2011). Research methods for the behavioral sciences (4th ed.). Mountain View, CA: Cengage.
A medida estatística mais comum do que a força das relações lineares entre variáveis é o coeficiente de correlação de Pearson, que é simbolizado pela letra r. O valor do coeficiente de correlação varia de r = -1.00 para r = +1.00., A direção da relação linear é indicada pelo sinal do coeficiente de correlação. Valores positivos de r (como r = .54 ou r = .67) indica que a relação é positiva linear (isto é, o padrão dos pontos na parcela de dispersão corre da parte inferior esquerda para a parte superior direita), enquanto valores negativos de r (como r = –.30 ou r = –.72) indica relações lineares negativas (isto é, os pontos correm da parte superior esquerda para a parte inferior direita). A força da relação linear é indexada pela distância do coeficiente de correlação de zero (seu valor absoluto)., Por exemplo, r= -.54 é uma relação mais forte do que r = .30, and r = .72 é uma relação mais forte do que r = –.57. Como o coeficiente de correlação de Pearson mede apenas relações lineares, variáveis que têm relações curvilíneas não são bem descritas por r, e a correlação observada será próxima de zero.também é possível estudar as relações entre mais de duas medidas ao mesmo tempo., A research design in which more than one predictor variable is used to predict a single outcome variable is analyzed through multiple regression (Aiken & West, 1991). Regressão múltipla é uma técnica estatística, baseada em coeficientes de correlação entre variáveis, que permite prever uma única variável de resultado de mais de uma variável de predictor. Por exemplo, a figura 2.11 “Prediction of Job Performance From Three Predictor Variables” mostra uma análise de regressão múltipla na qual três variáveis predictor são usadas para prever um único resultado., O uso de análise de regressão múltipla mostra uma vantagem importante de projetos de pesquisa correlacionados-eles podem ser usados para fazer previsões sobre a pontuação provável de uma pessoa em uma variável de resultado (por exemplo, desempenho de trabalho) com base no conhecimento de outras variáveis.
Figura 2.11 Previsão de Desempenho de Trabalho, a Partir de Três Variáveis preditoras
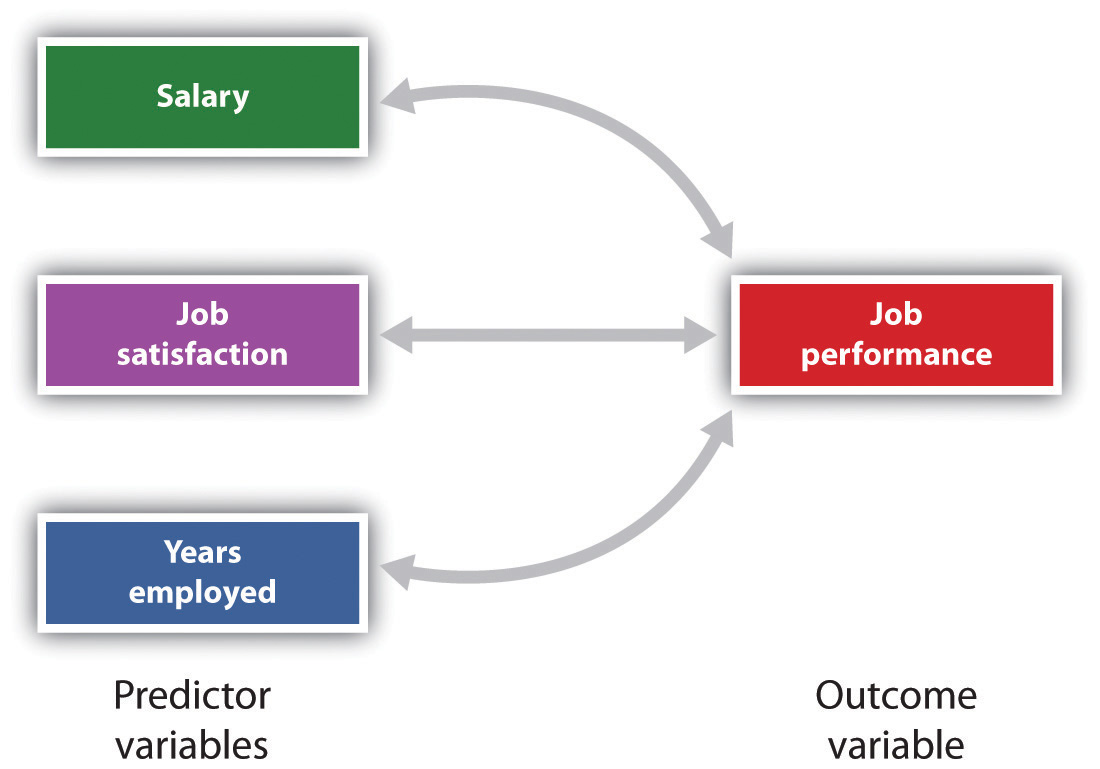
de regressão Múltipla permite aos cientistas prever os resultados em uma única variável de desfecho a utilização de mais de uma variável de previsão.,
uma limitação importante dos projetos de investigação correlacionados é que eles não podem ser usados para tirar conclusões sobre as relações causais entre as variáveis medidas. Considere, por exemplo, um pesquisador que tenha colocado a hipótese de que ver comportamento violento causará maior agressividade nas crianças. Ele coletou, de uma amostra de crianças do quarto ano, uma medida de quantos programas de televisão violentos cada criança vê durante a semana, bem como uma medida de quão agressivamente cada criança joga no playground da escola., A partir de seus dados coletados, o pesquisador descobre uma correlação positiva entre as duas variáveis medidas.
embora esta correlação positiva pareça apoiar a hipótese do pesquisador, não pode ser tomada para indicar que ver televisão violenta causa comportamento agressivo. Embora o pesquisador é tentado a supor que a visualização violentos de televisão faz com que um jogo agressivo,
Figura 2.2.2

há outras possibilidades., Uma possibilidade alternativa é que a direção causal é exatamente oposta ao que foi sugerido. Talvez as crianças que se comportaram de forma agressiva na escola desenvolver residual emoção que os leva a querer assistir a programas de televisão violentos em casa:
Figura 2.2.2

Embora essa possibilidade pode parecer menos provável, não há nenhuma forma de descartar a possibilidade de causalidade reversa na base desta correlação observada., Também é possível que ambos causal direções estão em funcionamento e que as duas variáveis fazer com que o outro:
Figura 2.2.2

Ainda outra possível explicação para a correlação observada é que tem sido produzida pela presença de um comum-causal variável (também conhecido como uma terceira variável)., Uma variável comum-causal é uma variável que não faz parte da hipótese de pesquisa, mas que causa tanto o preditor quanto a variável resultado e, portanto, produz a correlação observada entre eles. No nosso exemplo, uma potencial variável comum-causal é o estilo de disciplina dos Pais Das Crianças. Pais que usam um estilo de disciplina dura e punitiva podem produzir crianças que gostam de assistir televisão violenta e que se comportam agressivamente em comparação com crianças cujos pais usam uma disciplina menos dura:
figura 2.2.,2
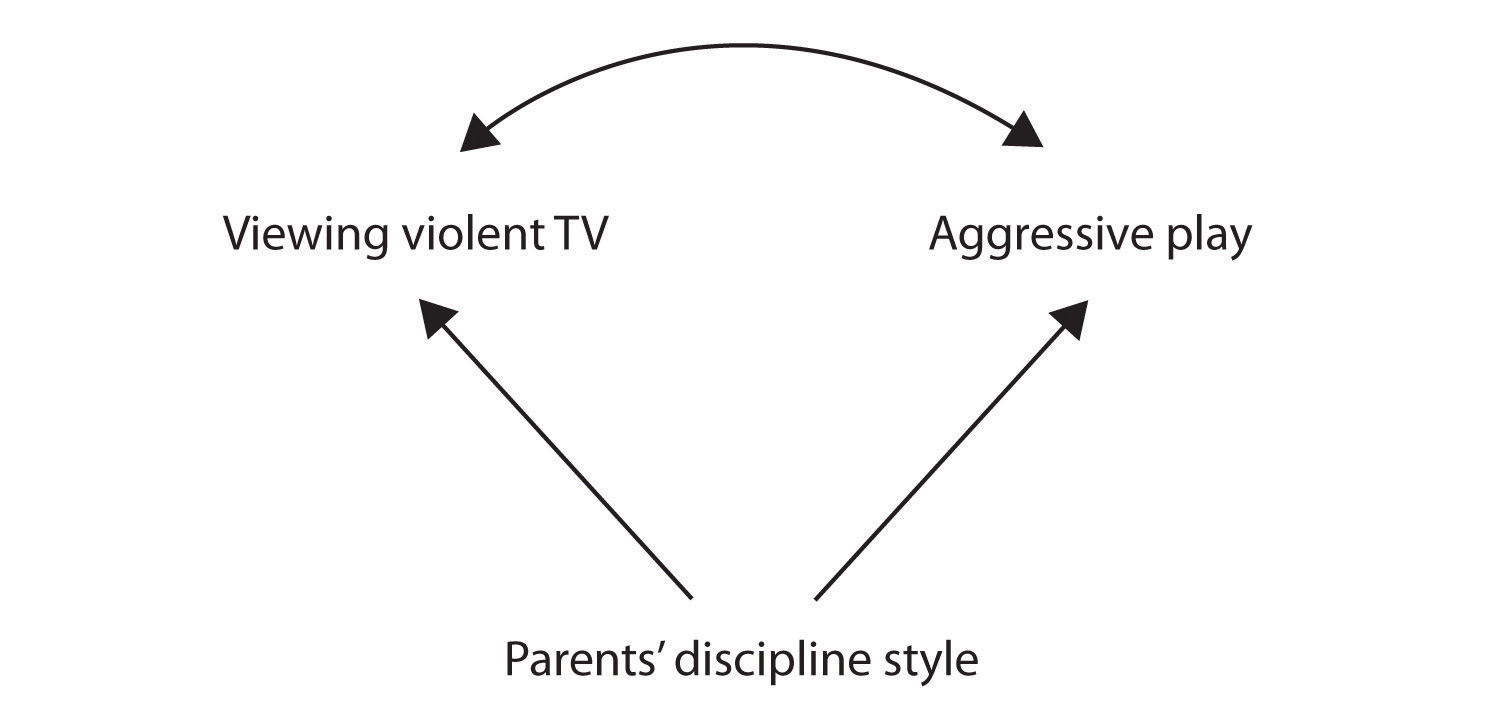
neste caso, a visualização de televisão e um jogo agressivo seria positivamente correlacionadas (como indicado pela seta curva entre eles), mesmo que nem um causou o outro, mas ambos foram causados por disciplina, o estilo dos pais (a reta setas). Quando as variáveis predictor e resultado são ambas causadas por uma variável comum-causal, a relação observada entre elas é dita espúria., Uma relação espúria é uma relação entre duas variáveis em que uma variável comum-causal produz e “explica” a relação. Se os efeitos da variável causal comum fossem retirados, ou controlados para, a relação entre o predictor e as variáveis de resultado desapareceria. No exemplo, a relação entre a agressão e a visualização da televisão pode ser espúria porque controlando para o efeito do estilo disciplinador dos pais, a relação entre a visualização da televisão e o comportamento agressivo pode desaparecer.,
variáveis causais comuns em projetos de pesquisa correlacional podem ser consideradas como variáveis “misteriosas” porque, como elas não foram medidas, sua presença e identidade são geralmente desconhecidas para o pesquisador. Uma vez que não é possível medir todas as variáveis que podem causar tanto as variáveis predictor quanto as variáveis de resultado, a existência de uma variável comum-causal desconhecida é sempre uma possibilidade. Por esta razão, ficamos com a limitação básica da pesquisa correlacional: correlação não demonstra causalidade., É importante que, ao ler sobre projetos de pesquisa correlacionados, você tenha em mente a possibilidade de relações espúrias, e certifique-se de interpretar os resultados adequadamente. Embora a pesquisa correlacional às vezes seja relatada como demonstrando causalidade sem qualquer menção à possibilidade de causalidade reversa ou variáveis causais comuns, consumidores informados de pesquisa, como você, estão cientes desses problemas interpretacionais.
Em suma, os projetos de pesquisa correlacional têm pontos fortes e limitações., Uma força é que eles podem ser usados quando a pesquisa experimental não é possível porque as variáveis predictor não podem ser manipuladas. Os projetos correlacionais também têm a vantagem de permitir que o pesquisador estude o comportamento como ocorre na vida cotidiana. E também podemos usar projetos correlacionais para fazer previsões—por exemplo, para prever a partir dos resultados de sua bateria de testes o sucesso dos estagiários de trabalho durante uma sessão de treinamento. Mas não podemos utilizar essas informações correlacionais para determinar se a formação causou um melhor desempenho no emprego. Para isso, os investigadores dependem de experiências.,