para usar a calculadora do ângulo de referência, basta introduzir qualquer ângulo na caixa do ângulo para encontrar o seu ângulo de referência, que é o ângulo agudo que corresponde ao ângulo introduzido. A calculadora aplica automaticamente as regras que vamos rever abaixo.
o que é um ângulo de referência?Imagine um plano de coordenadas. Digamos que queremos traçar um ângulo de 144° no nosso avião., Começamos do lado direito do eixo x, onde as três horas estão em um relógio. Rodamos no sentido anti-horário, que começa por subir. Continuamos indo além do ponto 90° (a parte superior do eixo y) até chegarmos a 144°. Desenhamos um raio da origem, que é o centro do avião, até aquele ponto. Agora temos um raio que chamamos de lado terminal. Mas precisamos de desenhar mais um raio para fazer um ângulo. Temos uma escolha neste momento. O nosso segundo raio tem de estar no eixo x. Se o tirarmos da origem para o lado direito, teremos desenhado um ângulo que mede 144°., Se o desenharmos para a esquerda, teremos desenhado um ângulo que mede 36°. Este segundo ângulo é o ângulo de referência. É sempre o menor dos dois ângulos, será sempre menor ou igual a 90°, e será sempre positivo. Aqui está uma animação que mostra um ângulo de referência para quatro ângulos diferentes, cada um dos quais está em um quadrante diferente. Repare como o segundo raio está sempre no eixo x.
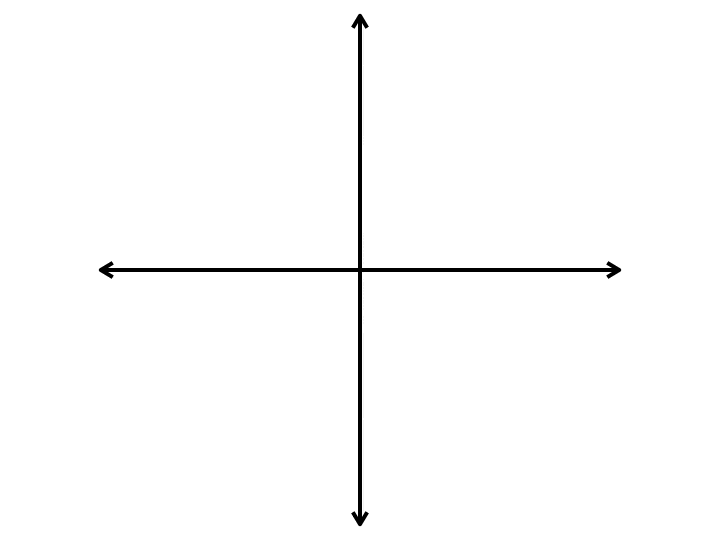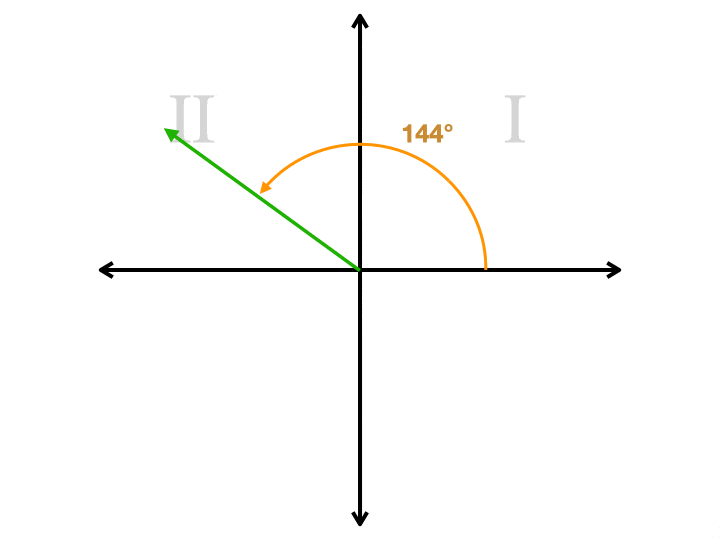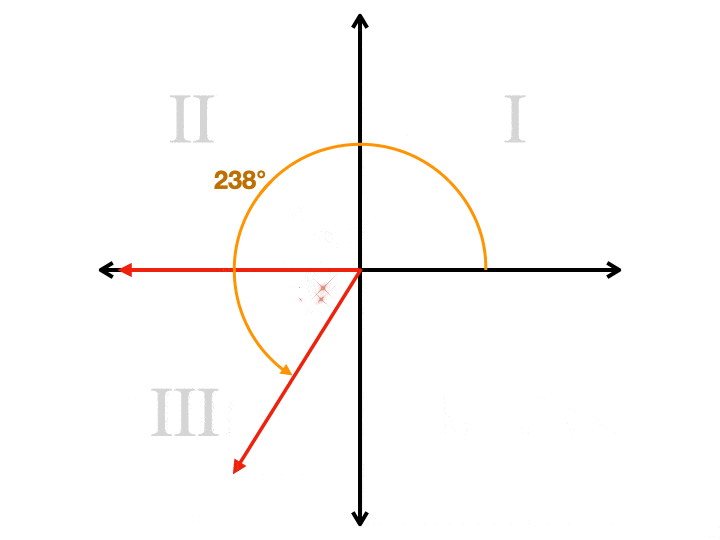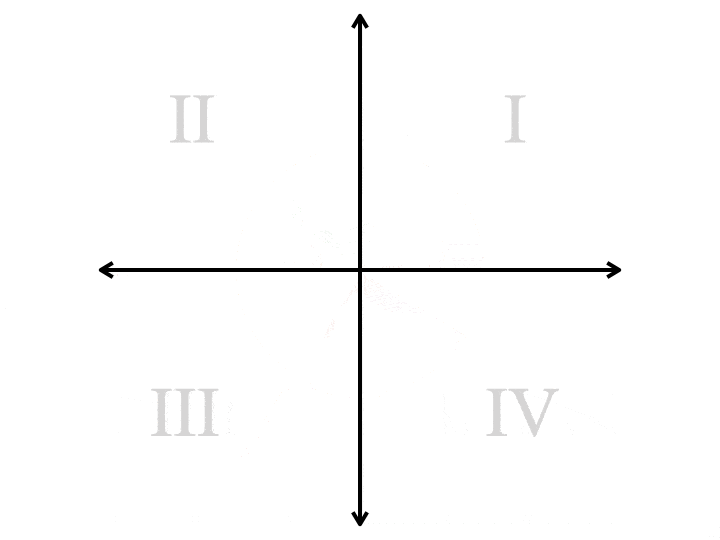
Como É Que o ângulo de referência é útil?
o ângulo de referência tem sempre os mesmos valores da função trigonometria que o ângulo original. Repare nos valores das palavras., O sinal pode não ser o mesmo, mas o valor sempre será. Isto é útil para ângulos comuns como 45° e 60° que vamos encontrar vezes sem conta. Uma vez que conhecemos seus valores seno, cosseno e tangente, também conhecemos os valores para qualquer ângulo cujo ângulo de referência é também 45° ou 60°. Quanto ao sinal, lembre-se que o seno é positivo no 1º e 2º quadrante e o cosseno é positivo no 1º e 4º quadrante.
Como É que encontramos o ângulo de referência sem uma calculadora?
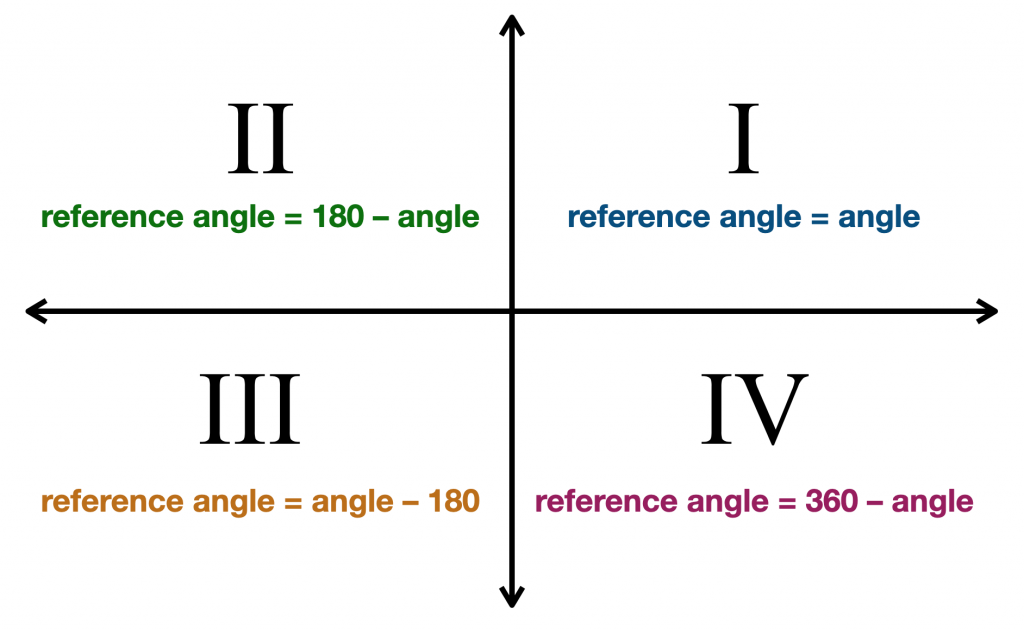
como encontramos o ângulo de referência depende do quadrante do lado terminal., quando o lado terminal está no primeiro quadrante (ângulos de 0 ° a 90°), o nosso ângulo de referência é o mesmo que o nosso ângulo dado. Isso faz sentido, uma vez que todos os ângulos no primeiro quadrante são inferiores a 90°. Então, se nosso ângulo dado é 33°, Então seu ângulo de referência é também 33°. quando o lado terminal está no segundo quadrante (ângulos de 90 ° a 180°), o nosso ângulo de referência é 180° menos o nosso ângulo dado. Então, se nosso ângulo dado é 110°, então seu ângulo de referência é 180 ° – 110 ° = 70°., quando o lado terminal está no terceiro quadrante (ângulos de 180 ° a 270°), o nosso ângulo de referência é o nosso ângulo dado menos 180°. Então, se nosso ângulo dado é 214°, então seu ângulo de referência é 214° – 180 ° = 34°. quando o lado terminal está no quarto quadrante (ângulos de 270° a 360°), o nosso ângulo de referência é de 360° menos o nosso ângulo dado. Então, se nosso ângulo dado é 332°, então seu ângulo de referência é 360 – – 332 ° = 28°.
e se o nosso Ângulo for maior que 360°?,
quando um ângulo é maior que 360°, isso significa que ele rodou todo o caminho em torno do plano de coordenadas e continuou em frente. Para encontrar o seu ângulo de Referência, primeiro precisamos de encontrar o seu ângulo correspondente entre 0° e 360°. Isto é fácil de fazer. Continuamos a subtrair 360 até estar abaixo dos 360. Por exemplo, se o nosso ângulo for 544°, subtraímos 360° dele para obter 184° (544° – 360° = 184°). Agora nós notaríamos que ele está no terceiro quadrante, então nós subtríamos 180° dele para descobrir que nosso ângulo de referência é 4°. e se o nosso Ângulo for negativo?,
quando um ângulo é negativo, nós movemos a outra direção para encontrar o nosso lado terminal. Isto significa que nos movemos no Sentido DOS ponteiros do relógio em vez de no sentido contrário ao dos ponteiros do relógio ao desenhá-lo. Ou podemos calculá-lo simplesmente adicionando-o a 360°. Por exemplo, se nosso ângulo dado for -110°, então nós o adicionaríamos a 360° para encontrar nosso ângulo positivo de 250° (-110° + 360° = 250°). Agora teríamos de ver que estamos no terceiro quadrante e aplicar essa regra para encontrar o nosso ângulo de referência.(250° – 180° = 70°).