aplicações do princípio de Pascal e sistemas hidráulicos
podemos derivar uma relação entre as forças neste sistema hidráulico simples aplicando o princípio de Pascal. Note primeiramente que os dois pistons no sistema estão na mesma altura, assim que não há nenhuma diferença na pressão devido a uma diferença na profundidade. A pressão devida ao F1 a actuar na área A1 é simplesmente
\(p_{1} = \frac{F_{1}}{a_{1}}}\), tal como definido por \(p = \frac{F}{a}\).,esta equação relaciona as relações força / área em qualquer sistema hidráulico, desde que os pistões estejam na mesma altura vertical e que o atrito no sistema seja negligenciável.os sistemas hidráulicos podem aumentar ou diminuir a força aplicada a eles. Para tornar a força maior, a pressão é aplicada a uma área maior. Por exemplo, se uma força de 100 N é aplicada ao cilindro esquerdo na figura 14.16 e o cilindro direito tem uma área cinco vezes maior, então a força de saída é de 500 N., Sistemas hidráulicos são análogos a Alavancas simples, mas eles têm a vantagem de que a pressão pode ser enviada através de linhas tortuosamente curvas para vários lugares ao mesmo tempo.o macaco hidráulico é um sistema hidráulico. Um macaco hidráulico é usado para levantar cargas pesadas, tais como as usadas pela mecânica automóvel para levantar um automóvel. É constituído por um fluido incompressível num tubo em U equipado com um pistão móvel de cada lado. Um lado do tubo U é mais estreito que o outro., Uma pequena força aplicada sobre uma pequena área pode equilibrar uma força muito maior do outro lado sobre uma área maior (figura \(\PageIndex{3}\)).
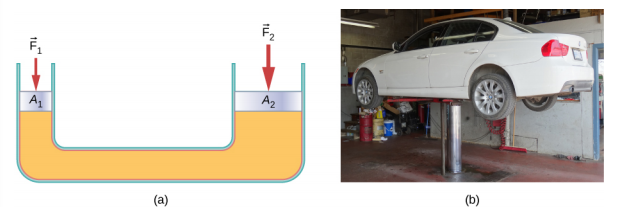
a Partir de Pascal princípio, pode ser mostrado que a força necessária para levantar o carro é menor que o peso do carro:
\
onde F1 é a força aplicada para levantar o carro, A1 é a área da seção transversal do pistão menor, A2 é a área da seção transversal do maior do pistão, e F2 é o peso do carro.exercício \(\PageIndex{1}\)
uma prensa hidráulica ainda funcionaria adequadamente se um gás fosse usado em vez de um líquido?