betrouwbaarheidsintervallen en p-waarden
om een discussie over statistische analyse mogelijk te maken, is het belangrijk om eerst het concept populatiestatistieken te begrijpen. Duidelijk, bevolkingsstatistieken zijn de waarden van om het even welke maatregel binnen de bevolking van belang, en het schatten van hen is het doel van de meeste studies ., Bijvoorbeeld, in een studie naar obesitas tarieven voor patiënten op een bepaalde medicatie, de populatie statistiek zou kunnen zijn de gemiddelde obesitas tarief voor alle patiënten op de medicatie.
voor het identificeren van deze waarde zijn echter gegevens nodig voor elk individu dat in deze categorie valt, wat onpraktisch is. In plaats daarvan kan een gerandomiseerde steekproef worden verzameld, waaruit steekproefstatistieken kunnen worden verkregen. Deze steekproefstatistieken dienen als schattingen van de overeenkomstige bevolkingsstatistieken en stellen een onderzoeker in staat conclusies te trekken over een populatie van belang.,
een significante beperking bestaat in die zin dat deze geconstrueerde monsters representatief moeten zijn voor de grotere populatie van belang. Hoewel er vele stappen zijn die kunnen worden genomen om deze beperking te verminderen, gaan de effecten (de zogenaamde steekproefbias ) soms buiten de controle van de onderzoeker. Bovendien, zelfs in een theoretische situatie zonder steekproefvooroordeel, kan randomisatie resulteren in een misrepresentatieve steekproef. In het vorige voorbeeld, stel dat de populatie van obesitas onder alle volwassenen die in aanmerking komen voor de medicatie was 25%., In een eenvoudige willekeurige steekproef van 30 patiënten uit deze populatie, is er een 19,7% kans dat ten minste 10 patiënten zwaarlijvig zullen zijn, resulterend in een steekproef Obesitas percentage van 33,3% of zelfs hoger. Zelfs als er geen verband tussen de medicatie en obesitas tarieven, is het nog steeds mogelijk om een tarief dat lijkt te verschillen van de totale obesitas tarief, die zich door willekeur in bemonstering alleen. Dit effect is de reden voor het rapporteren van betrouwbaarheidsintervallen en p-waarden in klinisch onderzoek.
betrouwbaarheidsintervallen zijn intervallen waarin de populatiestatistiek zou kunnen liggen., Zij zijn samengesteld op basis van de steekproefstatistiek en bepaalde kenmerken van de steekproef die meten hoe waarschijnlijk het representatief is en worden gerapporteerd tot een bepaalde drempelwaarde . Een 95% – betrouwbaarheidsinterval is een interval dat zo is geconstrueerd dat gemiddeld 95% van de aselecte steekproeven de werkelijke populatiestatistieken binnen hun 95% – betrouwbaarheidsinterval zouden bevatten. Een drempelwaarde voor significante resultaten wordt dus vaak op 95% gesteld, met dien verstande dat alle waarden binnen het gerapporteerde bereik even geldig zijn als de mogelijke populatiestatistiek.,
De p-waarde rapporteert vergelijkbare informatie op een andere manier. In plaats van een interval rond een steekproefstatistiek te construeren, rapporteert een p-waarde de waarschijnlijkheid dat de steekproefstatistiek werd geproduceerd uit willekeurige bemonstering van een populatie, gegeven een reeks veronderstellingen over de populatie, waarnaar wordt verwezen als de “nulhypothese” ., Als we de voorbeeldstudie over obesitas weer nemen, zou het obesitascijfer onder de steekproef (een steekproef van patiënten op de medicatie) kunnen worden gerapporteerd samen met een p-waarde die de kans bepaalt dat een dergelijk percentage kan worden veroorzaakt door een willekeurige steekproef van de totale populatie van patiënten die in aanmerking komen voor de medicatie. In het geval van de studie is de nulhypothese dat de populatiegraad van obesitas onder patiënten op de medicatie gelijk is aan de totale obesitas onder alle patiënten die in aanmerking komen voor de medicatie, dat wil zeggen, 25%., Een one-tailed p-waarde kan worden gebruikt als er reden is om te geloven dat een effect zou optreden in slechts één richting (bijvoorbeeld, kan er reden zijn om te geloven dat de medicatie gewichtstoename zou toenemen, maar niet afnemen), terwijl een two-tailed p-waarde moet worden gebruikt in alle andere gevallen. Bij gebruik van een symmetrische verdeling, zoals de normale verdeling, zijn tweestaart p-waarden gewoon tweemaal de éénstaart p-waarde.
stel nogmaals dat een steekproef van 30 patiënten die de medicatie gebruiken 12 personen met obesitas bevat. Bij een eenzijdige test is onze p-waarde 0,0216 (met behulp van de binomiale verdeling)., Zo kunnen we zeggen dat ons waargenomen percentage van 40% significant verschilt van het veronderstelde percentage van 25% bij een significantieniveau van 0,05. In een andere zin is het 95% betrouwbaarheidsinterval voor de waargenomen proportie 25,6% tot 61,07%. Betrouwbaarheidsintervallen komen overeen met tweestaarttests, waarbij een tweestaarttest wordt afgewezen als en alleen als het betrouwbaarheidsinterval de waarde van de nulhypothese niet bevat (in dit geval 25%).
als een berekende p-waarde klein is, is het waarschijnlijk dat de populatie niet gestructureerd is zoals oorspronkelijk vermeld in de nulhypothese., Als we een lage p-waarde krijgen, hebben we bewijs dat er een effect of reden was voor het waargenomen verschil – de medicatie, in dit geval. Een drempelwaarde van 0,05 (of 5%) wordt doorgaans gebruikt, waarbij een p-waarde onder deze drempel moet liggen om de overeenkomstige eigenschap statistisch significant te laten zijn.
Risicoratio ‘ s
risico, een andere term voor waarschijnlijkheid, is een ander fundamenteel principe van statistische analyse. Waarschijnlijkheid is een vergelijking van het observeren van een specifieke gebeurtenis die optreedt als gevolg van de totale unieke resultaten., Een munt flip is een triviaal voorbeeld: het risico van het observeren van een kop is ½ of 50%, Zoals van alle mogelijke unieke proeven (een flip resulteert in kop of een flip resulteert in staarten), slechts EEN is de gebeurtenis van belang (kop).
het gebruik van alleen risico maakt voorspellingen over een enkele populatie mogelijk. Bijvoorbeeld, kijkend naar obesitas tarieven binnen de bevolking van de V. S., meldde de CDC dat 42,4% van volwassenen zwaarlijvig waren in 2017-2018. Dus, het risico van een individu in de VS zwaarlijvig is rond 42,4% . Echter, de meeste studies kijken naar het effect van een specifieke interventie of een ander item (zoals mortaliteit) op een ander., Eerder veronderstelden we dat het Obesitas percentage van in aanmerking komende patiënten 25% was, maar hier gebruiken we de 42,4% geassocieerd met de Amerikaanse volwassen bevolking. Stel dat we een risico van 25% in een willekeurige steekproef van patiënten op de medicatie ook waarnemen. Om het effect van het medicijn op obesitas te conceptualiseren, zou een logische volgende stap het risico van obesitas in de Amerikaanse bevolking op het medicijn met het risico van obesitas in de Amerikaanse bevolking verdelen, wat in een risicoverhouding van 0.590 resulteert.,
deze berekening – een verhouding van twee risico ‘ s – is wat wordt bedoeld met de gelijknamige risk ratio (RR) statistiek, ook bekend als relatief risico. Hiermee kan een specifiek nummer worden gegeven voor hoeveel meer risico een individu in een categorie draagt in vergelijking met een individu in een andere categorie. In het voorbeeld, draagt een individu die het medicijn neemt 0,59 keer zoveel risico als een VOLWASSENE van de algemene bevolking van de V. S., We hebben echter aangenomen dat de bevolking die in aanmerking komt voor de medicatie een Obesitas – percentage van 25 procent had-misschien komt alleen een groep jonge volwassenen, die gemiddeld gezonder kunnen zijn, in aanmerking om de medicatie te nemen. Bij het onderzoeken van het effect van de medicatie op obesitas, dit is de verhouding die moet worden gebruikt als de nulhypothese. Als we een Obesitas percentage op de medicatie van 40%, met een p-waarde lager dan de significantieniveau van 0,05, dit is het bewijs dat de medicatie verhoogt het risico op obesitas (met een RR, in dit scenario, van 1,6)., Als zodanig is het belangrijk om de nulhypothese zorgvuldig te kiezen om relevante statistische voorspellingen te doen.
met RR betekent een resultaat van 1 dat beide groepen hetzelfde risico hebben, terwijl resultaten die niet gelijk zijn aan 1 erop wijzen dat de ene groep meer risico droeg dan de andere, een risico waarvan wordt aangenomen dat het te wijten is aan de interventie die in het onderzoek is onderzocht (formeel, de aanname van causale richting).
ter illustratie bekijken we de resultaten van een studie uit 2009 gepubliceerd in het Journal of Stroke and cerebrovasculaire Diseases., Het onderzoek meldt dat patiënten met een verlengd elektrocardiografisch QTc-interval meer kans hadden om binnen 90 dagen te sterven dan patiënten zonder een verlengd interval (relatief risico =2,5; 95% betrouwbaarheidsinterval 1,5-4,1) . Een betrouwbaarheidsinterval tussen 1,5 en 4,1 voor de risicoratio geeft aan dat patiënten met een verlengd QTc-interval 1,5-4,1 keer meer kans hadden om te sterven in 90 dagen dan patiënten zonder een verlengd QTc-interval.,
een tweede voorbeeld – in een baanbrekende paper die aantoonde dat de bloeddrukcurve bij acute ischemische beroerte U-vormig is in plaats van J-vormig , vonden de onderzoekers dat de RR bijna tweemaal zo hoog was bij patiënten met een gemiddelde arteriële bloeddruk (MAP) >140 mmHg of <100 mmHg (RR=1,8, 95% BI 1,1-2,9, p=0,027). Het hebben van een bi van 1,1-2,9 voor de RR betekent dat patiënten met een MAP buiten het bereik van 100-140 mmHg 1,1-2,9 keer meer kans hadden om te sterven dan degenen met een initiële MAP binnen dit bereik.,
bij een ander voorbeeld bleek uit een studie van 2018 onder Australische marinewerven dat degenen met geprefabriceerde orthesen (een soort voetsteun) een risico van 20,3% hadden op ten minste één nadelig effect, terwijl degenen zonder een risico van 12,4% hadden . Een risicoverhouding wordt hier gegeven door 0,203 / 0,124, of 1,63, wat erop wijst dat rekruten met voetorthesen 1,63 maal het risico van het hebben van een aantal nadelige gevolgen (b.v. voetblaar, pijn, enz.) dan die zonder. Dezelfde studie rapporteert echter een 95% betrouwbaarheidsinterval voor de risicoratio van 0,96 tot 2,76, met een p-waarde van 0,068., Kijkend naar het betrouwbaarheidsinterval, omvat het 95% gerapporteerde bereik (de algemeen aanvaarde standaard) waarden onder 1, 1 en waarden boven 1. Als je bedenkt dat alle waarden even waarschijnlijk de bevolkingsstatistiek zijn, met een betrouwbaarheid van 95%, is er geen manier om de mogelijkheid uit te sluiten dat Voet orthesen geen effect hebben, een significant voordeel hebben of een significant nadeel hebben. Bovendien is de p-waarde groter dan de standaard van 0,05, daarom leveren deze gegevens geen significant bewijs van voet orthesen die enig consistent effect hebben op bijwerkingen zoals blaren en pijn., Zoals eerder vermeld, is dit geen toeval – als ze worden berekend met behulp van dezelfde of soortgelijke methoden en de p-waarde is twee-tailed, betrouwbaarheidsintervallen en p-waarden zullen dezelfde resultaten rapporteren.
indien correct gebruikt, zijn risicoratio ‘ s een krachtige statistiek die een schatting in een populatie mogelijk maakt van de verandering in risico die een populatie draagt boven een andere., Ze zijn vrij gemakkelijk te begrijpen (de waarde is hoeveel keer het risico van een groep draagt over een andere), en met de aanname van causale richting, snel laten zien of een interventie (of andere geteste variabele) heeft een effect op de resultaten.
Er zijn echter beperkingen. Ten eerste kunnen RR ‘ s niet in alle gevallen worden toegepast. Aangezien het risico in een steekproef een schatting van het risico in een populatie is, moet de steekproef redelijk representatief zijn voor de populatie. Als zodanig kan bij casestudy ‘s, enkel op grond van het feit dat de ratio’ s van de uitkomsten worden gecontroleerd, geen risicoverhouding worden gerapporteerd., Ten tweede is RR, zoals bij alle hier besproken statistieken, een relatieve maatstaf, die informatie verschaft over het risico in de ene groep ten opzichte van de andere. Het probleem hier is dat een studie waarbij twee groepen een risico van 0,2% en 0,1% hadden, dezelfde RR 2 draagt als een studie waarbij twee groepen een risico van 90% en 45% hadden. Hoewel het in beide gevallen waar is dat degenen met de interventie twee keer het risico liepen, komt dit neer op slechts 0,1% meer risico in het ene geval en 45% meer risico in het andere geval., Het rapporteren van alleen de RR overdrijft het effect in eerste instantie, terwijl het effect in tweede instantie mogelijk zelfs minimaliseert (of op zijn minst decontextualiseert).
Odds ratio ‘ s
terwijl risk het aantal interessante gebeurtenissen rapporteert in verhouding tot het totale aantal onderzoeken, rapporteren odds het aantal interessante gebeurtenissen in relatie tot het aantal niet-interessante gebeurtenissen. Anders gesteld, het rapporteert het aantal gebeurtenissen aan Niet-gebeurtenissen., Terwijl het risico, zoals eerder bepaald, van het omgooien van een munt om kop is 1: 2 of 50%, de kans van het omgooien van een munt om kop is 1:1, omdat er een gewenste uitkomst (gebeurtenis), en een ongewenste uitkomst (niet-gebeurtenis) (figuur 1).
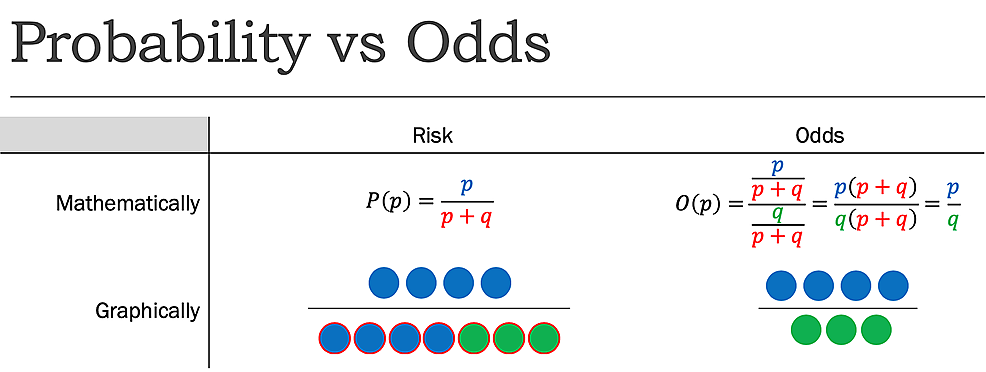
figuur 1:waarschijnlijkheid (P) vs.kansen (O) waarbij p=kans op succes en q=kans op falen
net als bij RR, waarbij de verhouding van twee risico ‘ s werd genomen voor twee afzonderlijke groepen; een ratio van twee odds kan worden genomen voor twee afzonderlijke groepen om een odds ratio (or) te produceren., In plaats van te rapporteren hoeveel keer het risico een groep draagt ten opzichte van de andere, het rapporteert hoe vaak de kansen een groep draagt naar de andere.
voor de meesten is dit een moeilijker te begrijpen statistiek. Risico is vaak een meer intuïtief concept dan odds, en dus het begrijpen van relatieve risico ‘ s wordt vaak de voorkeur boven het begrijpen van relatieve odds. Echter, of lijdt niet aan dezelfde causale aanname beperkingen als RR, waardoor het breder toepasbaar.,
bijvoorbeeld, odds zijn een symmetrische maat, wat betekent dat terwijl risk alleen resultaten onderzoekt gegeven interventies, odds ook interventies gegeven resultaten kan onderzoeken. Aldus, kan een studie worden geconstrueerd waar, eerder dan het kiezen van proefgroepen en het meten van resultaten, resultaten kunnen worden gekozen, en andere factoren kunnen worden geanalyseerd. Hieronder volgt een voorbeeld van een casestudy, een situatie waarin RR niet kan worden gebruikt, maar wel kan worden gebruikt.
een 2019 case-control studie bewijst een goed voorbeeld., Op zoek naar mogelijke correlatie tussen een hepatitis A virus (HAV) infectie prominent in Canada en sommige veroorzakende factor, werd een studie geconstrueerd op basis van de uitkomst (met andere woorden, individuen werden gecategoriseerd op basis van hun HAV status, als de “interventie”, of causale gebeurtenis, was onbekend). De studie keek naar degenen met HAV en degenen zonder en welk voedsel ze hadden gegeten voorafgaand aan HAV infectie . Uit dit, meerdere odds ratio ‘ s werden geconstrueerd vergelijken van een specifiek voedsel item HAV status., Uit de gegevens bleek bijvoorbeeld dat onder de proefpersonen die aan garnalen/garnalen waren blootgesteld, acht positief waren voor HAV en zeven niet, terwijl voor degenen zonder blootstelling twee positief waren voor HAV en 29 niet. Een odds ratio wordt genomen door (8:7)/(2:29) dat is ongeveer 16,6. De studiegegevens rapporteerden een OR van 15,75, met de kleine discrepantie waarschijnlijk afkomstig van eventuele pre-berekening aanpassingen voor verstorende variabelen die niet in de paper werd besproken. Een p-waarde van 0,01 werd gerapporteerd, waardoor statistisch bewijs hiervoor werd geleverd of significant was.,
Dit kan op twee gelijke manieren geïnterpreteerd worden. Ten eerste zijn de kansen van garnalen/garnalen blootstelling voor degenen met HAV 15,75 keer hoger dan voor degenen zonder. Op gelijke wijze is de kans voor HAV-posiitve versus HAV-negatief 15,75 keer hoger voor degenen die aan garnalen/garnalen worden blootgesteld dan voor degenen die niet worden blootgesteld.
Totaal, of geeft een maat voor de sterkte van associatie tussen twee variabelen op een schaal van 1 is geen associatie, boven 1 is een positieve associatie, en onder 1 is een negatieve associatie., Hoewel de voorgaande twee interpretaties juist zijn, zijn ze niet zo direct begrijpelijk als een RR zou zijn geweest, als het mogelijk was geweest er een te bepalen. Een alternatieve interpretatie is dat er een sterke positieve correlatie bestaat tussen de blootstelling aan garnalen en HAV.
daarom is het in sommige specifieke gevallen passend om RR te benaderen met OR. In dergelijke gevallen moet de aanname van zeldzame ziekten aanhouden. Dat wil zeggen, een ziekte moet zeer zeldzaam zijn binnen een populatie., Onder dit geval, benadert het risico van de ziekte binnen de bevolking (p/(p+q)) de kansen van de ziekte binnen de bevolking (p/q) aangezien p onbeduidend klein ten opzichte van q wordt. Echter, als deze aanname faalt, wordt het verschil steeds meer overdreven. Wiskundig gezien verhoogt het verlagen van p in P + q onderzoeken de q om dezelfde totale onderzoeken te behouden. Bij risico verandert alleen de teller, terwijl bij kansen zowel de teller als de noemer in tegengestelde richtingen veranderen., Als gevolg hiervan zal de OR voor gevallen waarin de RR en / of beide lager zijn dan 1, de RR onderschatten, terwijl voor gevallen waarin beide hoger zijn dan 1, de OR de RR overschat.
foutief rapporteren van de OK als de RR kan dan vaak gegevens overdrijven. Het is belangrijk om te onthouden dat of is een relatieve maat net als RR, en dus soms een grote of kan corresponderen met een klein verschil tussen kansen.
voor de meest getrouwe rapportage, dan, of mag niet worden gepresenteerd als een RR, en mag alleen worden gepresenteerd als een benadering van RR als de aanname van zeldzame ziekten redelijkerwijs kan houden., Indien mogelijk moet altijd een RR worden gerapporteerd.
Hazard ratio ‘ s
zowel RR als OR hebben betrekking op interventies en resultaten, en rapporteren dus over een volledige studieperiode. Een vergelijkbare, maar duidelijke maatstaf, de hazard ratio (HR), heeft echter betrekking op de veranderingspercentages (Tabel 1).
| RR | of | HR | doel | Bepaal de relatie in risicostatus op basis van een variabele. | Bepaal de associatie tussen twee variabelen., | bepaal hoe een groep ten opzichte van een andere verandert. |
| gebruik | vertelt ons hoe een interventie risico ‘ s verandert. | vertelt ons of er een verband is tussen een interventie en risico; schat hoe deze associatie van toepassing is. | vertelt ons hoe een interventie de snelheid van het ervaren van een gebeurtenis verandert. |
| beperkingen | alleen van toepassing als de onderzoeksopzet representatief is voor de populatie. Kan niet worden gebruikt bij case-control studies. | kan over het algemeen overal worden toegepast, maar niet altijd een nuttige statistiek zelf. Overdrijft risico ‘ s., | om typisch nuttig te zijn, moet het tempo van verandering binnen twee groepen relatief consistent zijn. |
| tijdlijn | statisch-houdt geen rekening met percentages. Vat een algemene studie samen. | statisch-houdt geen rekening met percentages. Vat een algemene studie samen. | gebaseerd op percentages. Geeft informatie over de manier waarop een studie vordert in de tijd. |
Tabel 1: relatieve risico (RR) vs. Odds Ratio (OR) vs., Hazard Ratio (HR)
uur komen samen met overlevingscurves, die de temporele progressie van een gebeurtenis binnen een groep laten zien, of dat nu overlijden is of het oplopen van een ziekte. In een overlevingscurve komt de verticale as overeen met de gebeurtenis van belang en de horizontale as correspondeert met de tijd. Het gevaar van de gebeurtenis is dan gelijk aan de helling van de grafiek, of de gebeurtenissen per keer.
een hazard ratio is gewoon een vergelijking van twee gevaren., Het kan laten zien hoe snel twee survivorship curves verschillen door vergelijking van de hellingen van de curves. Een HR van 1 geeft geen divergentie aan-binnen beide curven was de waarschijnlijkheid van de gebeurtenis op een bepaald moment even waarschijnlijk. Een HR die niet gelijk is aan 1 geeft aan dat twee gebeurtenissen niet in gelijke mate plaatsvinden en dat het risico van een individu in de ene groep verschilt van het risico van een individu in een andere groep op een bepaald tijdsinterval.
een belangrijke aanname die HRs maakt is de proportionele aanname., Om een bijzondere hazard ratio te rapporteren, moet ervan worden uitgegaan dat de twee Hazard rates constant zijn. Als de helling van de grafiek moet veranderen, zal de verhouding ook veranderen in de tijd, en zal dus niet van toepassing zijn als een vergelijking van waarschijnlijkheid op een bepaald moment.
overweeg het onderzoek met een nieuw chemotherapeutisch middel om de levensverwachting van patiënten met een specifieke kanker te verlengen. In zowel de interventie-als de controlegroep was in week 40 25% overleden., Aangezien beide groepen daalden van 100% overleving tot 75% overleving over de periode van 40 weken, zouden de hazard rates gelijk zijn en dus de hazard rates gelijk aan 1. Dit suggereert dat een persoon die het medicijn ontvangt net zo waarschijnlijk zal sterven als iemand die het medicijn op elk moment niet ontvangt.
Het is echter mogelijk dat in de interventiegroep alle 25% stierf tussen week 6 en 10, terwijl in de controlegroep alle 25% stierf binnen week 1 tot 6. In dit geval zou het vergelijken van medianen een hogere levensverwachting geven voor degenen die het medicijn gebruiken, ondanks dat de HR geen verschil vertoont., In dit geval faalt de aanname van proportionele gevaren, aangezien de gevarenpercentages in de loop van de tijd (vrij dramatisch) veranderen. In dergelijke gevallen is HR niet van toepassing.
omdat het soms moeilijk is om vast te stellen of de aanname van proportionele gevaren redelijk van toepassing is, en omdat het nemen van een HR de oorspronkelijke meting (hazard rates) van de tijdseenheid verbreekt, is het gebruikelijk om HR samen met de mediane tijden te rapporteren.,
In een studie ter evaluatie van de prognostische prestaties van De Rapid Emergency Medicine Score (REMS) en de Worthing Fysiologische Scoring system (WPSS), de onderzoekers van mening dat het risico van de 30-dagen mortaliteit was verhoogd met 30% voor elke extra REMS-eenheid (HR: 1.28; 95% confidence interval (CI): 1.23-1.34) en 60% voor elke extra WPSS eenheid (HR: 1.6; 95% CI: 1.5-1.7). In dit geval veranderde het sterftecijfer niet, maar het scoresysteem om het te voorspellen wel, zodat de HR kan worden gebruikt. Met een betrouwbaarheidsinterval tussen 1,5 en 1.,7 voor de wpss hazards ratio geeft aan dat de mortaliteitscurve voor mensen met een hogere WPS sneller afneemt (ongeveer 1,5-1,7 keer). Aangezien het lage einde van het interval nog steeds boven 1 ligt, zijn we ervan overtuigd dat het werkelijke risico van overlijden binnen 30 dagen hoger is voor de groep met hogere WPS .
in een studie van 2018 over het drinken van binge bij personen met bepaalde risicofactoren, werd een overlevingscurve geconstrueerd die de snelheid van het bereiken van binge drinken voor controlepersonen, die met een familiegeschiedenis, mannelijk geslacht, die met een hoge impulsiviteit, en die met een hogere respons op alcohol beschrijft., Voor mannen en mensen met een familiegeschiedenis werd statistisch significant bewijs gerapporteerd voor een hoger percentage van het bereiken van binge drinking (een HR van 1,74 voor mannen en 1,04 voor mensen met een familiegeschiedenis) . Voor degenen met een hoge impulsiviteit, hoewel de HR 1,17 was, varieerde het 95% betrouwbaarheidsinterval van 1,00 tot 1,37. Bij een betrouwbaarheidsniveau van 95% is het dus onmogelijk uit te sluiten dat de HR 1,00 was.,
vanwege de aanwezige overdrijving is het belangrijk om te voorkomen dat UPR ’s als RR’ s worden weergegeven, en evenzo is het belangrijk om te erkennen dat een gerapporteerde of zelden een goede benadering van relatieve risico ‘ s biedt, maar eerder gewoon een maat voor correlatie geeft.
vanwege zijn vermogen om duidelijke conclusies te trekken en begrijpelijkheid, moet RR indien mogelijk worden gerapporteerd, maar in gevallen waarin de causaliteitsaanname wordt geschonden (zoals casuscontrolestudies en logistieke regressie), of kan worden gebruikt.,
uur worden gebruikt bij overlevingscurven en er wordt van uitgegaan dat de gevarentarieven in de loop van de tijd gelijk zijn. Hoewel het nuttig is om twee percentages te vergelijken, moeten ze worden gerapporteerd met mediane tijden om de proportionele aanname van gevaren te rechtvaardigen.
ten slotte mag, ongeacht de waarde van de HR/RR/of statistiek, alleen een interpretatie worden gegeven nadat is bepaald of het resultaat statistisch significant bewijs levert voor een conclusie (zoals bepaald door de p-waarde of het betrouwbaarheidsinterval)., Het onthouden van deze principes en het kader van HR/RR/of minimaliseert verkeerde voorstelling en voorkomt dat men onjuiste conclusies trekt uit de resultaten van een gepubliceerde studie betreffende verschillende monsters. Figuur 2 vat correct en onjuist gebruik van deze verschillende risicoratio ‘ s samen.
