om de referentiehoekcalculator te gebruiken, voert u eenvoudig een willekeurige hoek in in het vak hoek om de referentiehoek te vinden, wat de scherpe hoek is die overeenkomt met de ingevoerde hoek. De calculator past automatisch de regels toe die we hieronder zullen bekijken.
Wat is een referentiehoek?
stel je een coördinatenvlak voor. Laten we zeggen dat we een hoek willen tekenen die 144° is op ons vlak., We beginnen aan de rechterkant van de x-as, waar drie uur op een klok staat. We draaien tegen de klok in, wat begint met omhoog bewegen. We blijven voorbij het 90° punt (het bovenste deel van de y-as) tot we bij 144°komen. We tekenen een straal van de oorsprong, die het centrum van het vlak is, tot dat punt. Nu hebben we een straal die we de terminal kant noemen. Maar we moeten nog een straal tekenen om een hoek te maken. We hebben nu een keuze. Onze tweede straal moet op de x-as staan. Als we het van de oorsprong naar de rechterkant tekenen, hebben we een hoek getekend die 144°meet., Als we het naar links tekenen, hebben we een hoek getekend die 36°meet. Deze tweede hoek is de referentiehoek. Het is altijd de kleinste van de twee hoeken, zal altijd kleiner zijn dan of gelijk aan 90°, en het zal altijd positief zijn. Hier is een animatie die een referentiehoek toont voor vier verschillende hoeken, die elk in een ander kwadrant staan. Merk op hoe de tweede straal altijd op de x-as staat.
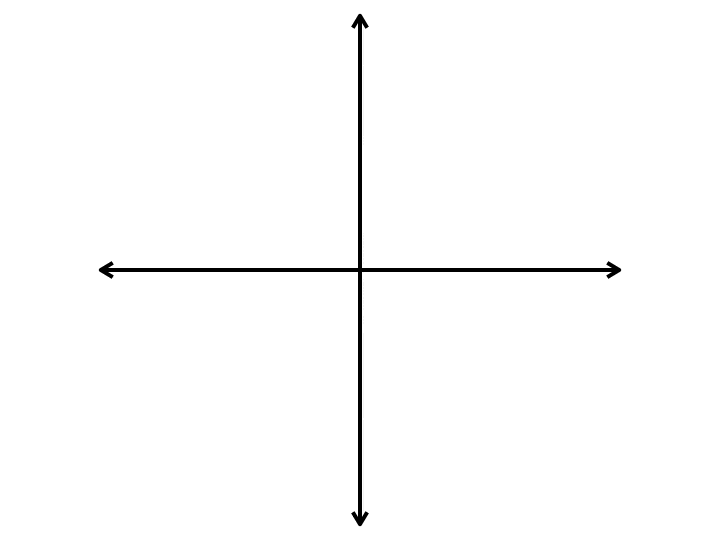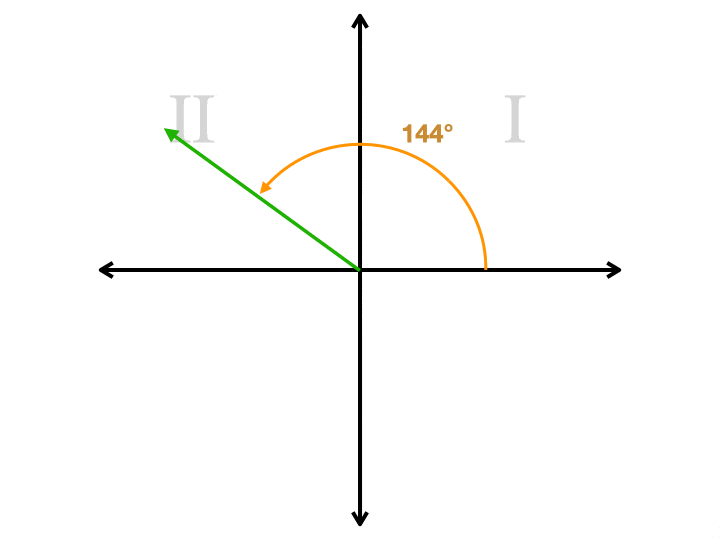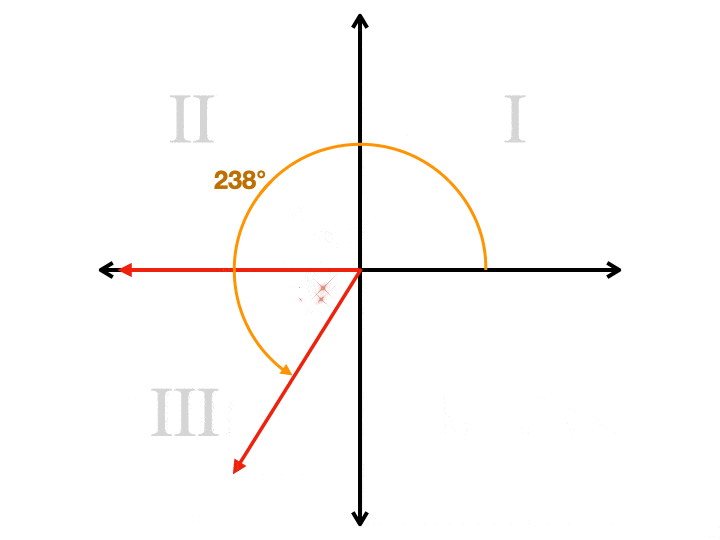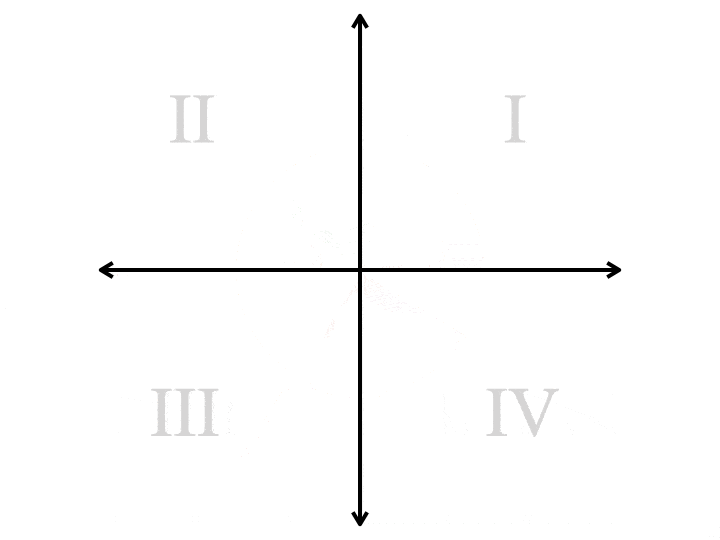
Hoe is de referentiehoek nuttig?
de referentiehoek heeft altijd dezelfde trig functiewaarden als de oorspronkelijke hoek. Let op het woord waarden daar., Het teken mag dan niet hetzelfde zijn, maar de waarde zal dat altijd zijn. Dit is handig voor gemeenschappelijke hoeken zoals 45° en 60° die we steeds weer tegenkomen. Zodra we hun sinus -, cosinus-en raakwaarden kennen, weten we ook de waarden voor elke hoek waarvan de referentiehoek ook 45° of 60°is. Wat het teken betreft, onthoud dat sinus positief is in het 1e en 2e kwadrant en cosinus positief is in het 1e en 4e kwadrant.
hoe vinden we de referentiehoek zonder rekenmachine?
hoe we de referentiehoek vinden hangt af van de kwadrant van de eindzijde.,
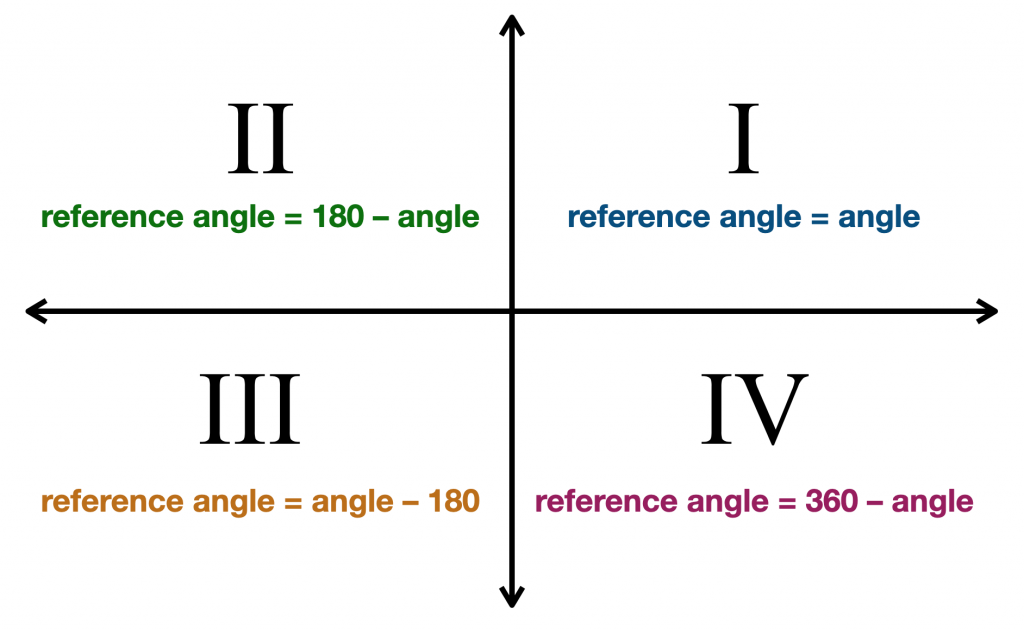
wanneer de eindzijde zich in het eerste kwadrant bevindt (hoeken van 0° tot 90°), is onze referentiehoek dezelfde als onze gegeven hoek. Dit is logisch, omdat alle hoeken in het eerste kwadrant kleiner zijn dan 90°. Dus, als onze gegeven hoek 33° is, dan is zijn referentiehoek ook 33°.
wanneer de eindzijde zich in het tweede kwadrant bevindt (hoeken van 90° tot 180°), is onze referentiehoek 180° min onze gegeven hoek. Dus, als onze gegeven hoek 110° is, dan is zijn referentiehoek 180° – 110° = 70°.,
wanneer de eindzijde zich in het derde kwadrant bevindt (hoeken van 180° tot 270°), is onze referentiehoek onze gegeven hoek minus 180°. Dus, als onze gegeven hoek 214° is, dan is zijn referentiehoek 214° – 180° = 34°.
wanneer de eindzijde zich in het vierde kwadrant bevindt (hoeken van 270° tot 360°), is onze referentiehoek 360° min onze gegeven hoek. Dus, als onze gegeven hoek 332° is, dan is de referentiehoek 360° – 332° = 28°.
wat als onze hoek groter is dan 360°?,
wanneer een hoek groter is dan 360°, betekent dit dat deze helemaal rond het coördinatenvlak gedraaid is en doorgegaan is. Om de referentiehoek te vinden, moeten we eerst de overeenkomstige hoek tussen 0° en 360°vinden. Dit is makkelijk te doen. We blijven er 360 van aftrekken tot het onder 360 is. Bijvoorbeeld, als onze Hoek 544° is, zouden we 360° ervan aftrekken om te krijgen 184° (544° – 360° = 184°). Nu zouden we merken dat het in het derde kwadrant is, dus we zouden er 180° van Aftrekken om te zien dat onze referentiehoek 4°is.
wat als onze Hoek negatief is?,
wanneer een hoek negatief is, bewegen we de andere richting om onze terminal kant te vinden. Dit betekent dat we bij het tekenen met de klok mee bewegen in plaats van tegen de klok in. Of we kunnen het berekenen door het gewoon op te tellen tot 360°. Bijvoorbeeld, als onze gegeven hoek -110° is, dan zouden we het toevoegen aan 360° om onze positieve hoek van 250° (-110° + 360° = 250°). Nu moeten we zien dat we in het derde kwadrant zijn en die regel toepassen om onze referentiehoek te vinden.(250° – 180° = 70°).