Public Key Cryptography
In tegenstelling tot symmetrische sleutel cryptografie, vinden we geen historisch gebruik van public-key cryptografie. Het is een relatief nieuw concept.
symmetrische cryptografie was zeer geschikt voor organisaties zoals overheden, militairen en grote financiële ondernemingen die betrokken waren bij de geclassificeerde communicatie.,
met de verspreiding van meer onveilige computernetwerken in de afgelopen decennia, werd een echte behoefte gevoeld om cryptografie op grotere schaal te gebruiken. De symmetrische sleutel bleek niet praktisch te zijn vanwege de uitdagingen voor het sleutelbeheer. Dit leidde tot de publieke sleutel cryptosystemen.
het proces van encryptie en decryptie wordt weergegeven in de volgende afbeelding −
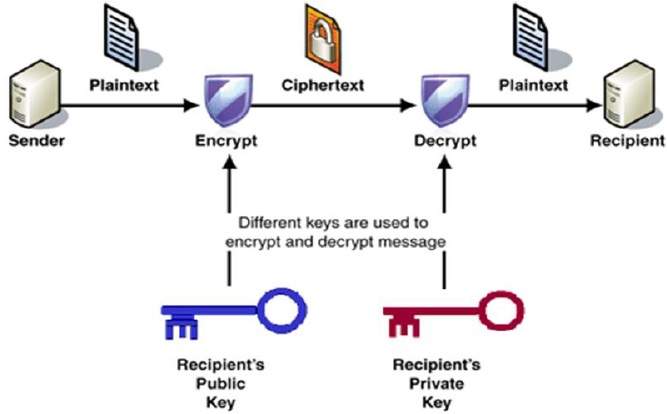
De belangrijkste eigenschappen van public key encryptie schema zijn −
-
verschillende sleutels worden gebruikt voor encryptie en decryptie., Dit is een eigenschap die dit schema anders stelt dan symmetrische encryptie schema.
-
elke ontvanger beschikt over een unieke decryptie sleutel, meestal aangeduid als zijn persoonlijke sleutel.
-
ontvanger moet een versleutelingssleutel publiceren, aangeduid als zijn publieke sleutel.
-
enige zekerheid van de authenticiteit van een publieke sleutel is nodig in dit schema om spoofing door tegenstander als de ontvanger te voorkomen. In het algemeen, dit type cryptosysteem omvat vertrouwde derde partij die certificeert dat een bepaalde publieke sleutel behoort tot een specifieke persoon of entiteit alleen.,het versleutelingsalgoritme van
-
is complex genoeg om de aanvaller te verbieden de platte tekst af te leiden uit de versleutelingstekst en de versleutelingssleutel.
-
hoewel private en publieke sleutels wiskundig gerelateerd zijn, is het niet haalbaar om de private sleutel uit de publieke sleutel te berekenen. In feite is het intelligente deel van elk public-key cryptosysteem het ontwerpen van een relatie tussen twee sleutels.
er zijn drie soorten versleutelingsschema ‘ s voor openbare sleutels., We bespreken ze in de volgende secties –
RSA cryptosysteem
Dit cryptosysteem is een van de eerste systemen. Het blijft de meest gebruikte cryptosysteem zelfs vandaag. Het systeem werd uitgevonden door drie geleerden Ron Rivest, Adi Shamir, en Len Adleman en dus, het wordt aangeduid als RSA cryptosystem.
We zullen twee aspecten van het RSA cryptosysteem zien, ten eerste het genereren van sleutelparen en ten tweede encryptie-decryptie algoritmen.,
generatie van RSA-sleutelpaar
elke persoon of partij die wil deelnemen aan communicatie met behulp van encryptie moet een sleutelpaar genereren, namelijk publieke en private sleutel. Het proces dat wordt gevolgd bij het genereren van sleutels wordt hieronder beschreven −
-
Genereer de RSA-modulus (n)
-
Selecteer twee grote priemgetallen, p en q.
-
Bereken n=p*q. voor sterke onbreekbare encryptie, laat n een groot aantal zijn, meestal een minimum van 512 bits.,
-
-
afgeleid nummer (e)
-
nummer E moet groter zijn dan 1 en kleiner dan (p − 1)(q − 1).
-
er mag geen gemeenschappelijke factor zijn voor e en (p − 1)(q − 1), behalve voor 1. Met andere woorden twee getallen e en (p – 1)(q – 1) zijn coprime.
-
-
vorm de publieke sleutel
-
het nummerpaar (n, e) vormt de publieke sleutel van de RSA en wordt openbaar gemaakt.,
-
interessant is dat, hoewel n deel uitmaakt van de publieke sleutel, moeilijkheden bij het factoriseren van een groot priemgetal ervoor zorgen dat aanvaller niet in eindige tijd de twee priemgetallen (p & q) kan vinden die gebruikt worden om n te verkrijgen. Dit is de sterkte van RSA.
-
-
Genereer de private sleutel
-
Private sleutel D wordt berekend uit p, q en e. voor gegeven n en e is er uniek nummer d.
-
getal D is de inverse van e modulo (p-1) (q – 1)., Dit betekent dat d het getal kleiner is dan (p-1) (q – 1), zodat het, vermenigvuldigd met e, gelijk is aan 1 modulo(p – 1) (q – 1).
-
Deze relatie wordt wiskundig als volgt geschreven –
-
ed = 1 mod (p − 1)(q − 1)
het uitgebreide Euclidische algoritme neemt p, q en e als invoer en geeft d als uitvoer.
voorbeeld
een voorbeeld van het genereren van RSA sleutelpaar wordt hieronder gegeven. (Voor een beter begrip zijn de hier genomen priemgetallen p & q kleine waarden. In de praktijk zijn deze waarden zeer hoog).,
-
laat twee priemgetallen p = 7 en q = 13 zijn. Dus, modulus n = pq = 7 x 13 = 91.
-
Select e = 5, wat een geldige keuze is omdat er geen getal is dat een gemeenschappelijke factor is van 5 en (p − 1)(q− 1) = 6 × 12 = 72, behalve 1.
-
het nummerpaar (n, e) = (91, 5) vormt de publieke sleutel en kan beschikbaar worden gesteld aan iedereen die we versleutelde berichten willen kunnen sturen.
-
invoer P = 7, q = 13, en e = 5 in het uitgebreide Euclidische algoritme. De uitvoer is d = 29.,
-
Controleer of de berekende d correct is door berekening –
de = 29 × 5 = 145 = 1 mod 72
-
vandaar dat publieke sleutel (91, 5) is en private sleutels (91, 29).
encryptie en decryptie
zodra het sleutelpaar is gegenereerd, is het proces van encryptie en decryptie relatief eenvoudig en berekenbaar eenvoudig.
interessant is dat RSA niet direct werkt op strings van bits zoals in het geval van symmetrische sleutelversleuteling. Het werkt op getallen modulo n. daarom is het noodzakelijk om de platte tekst weer te geven als een reeks getallen kleiner dan n.,
RSA-versleuteling
-
stel dat de afzender een sms-bericht wil sturen naar iemand met een publieke sleutel (n, e).
-
De afzender dan is de klare tekst als een reeks getallen kleiner dan n.
-
Voor het coderen van de eerste plaintext P, dat is een getal modulo n. De encryptie proces is eenvoudig wiskundige stap −
C = Pe mod n
-
In andere woorden, de cijfertekst C is gelijk aan de plaintext P vermenigvuldigd met zichzelf e keer en dan gereduceerd modulo n. Dit betekent dat C is ook een getal kleiner dan n.,
-
terugkerend naar ons Sleutelgeneratievoorbeeld met platte tekst P = 10, krijgen we versleuteling C −
C = 105 mod 91
RSA decryptie
-
het decryptieproces voor RSA is ook zeer eenvoudig. Stel dat de ontvanger van een publiek-sleutelpaar (n, e) een cijfertekst C heeft ontvangen.
-
ontvanger verhoogt C tot de macht van zijn privésleutel d. het resultaat modulo n zal de platte tekst P. zijn,
Plaintext = Cd mod n
-
terugkerend naar ons numerieke voorbeeld, zou de versleuteling C = 82 gedecodeerd worden naar nummer 10 met behulp van private key 29 −
Plaintext = 8229 mod 91 = 10
RSA analyse
de beveiliging van RSA hangt af van op de sterke punten van twee afzonderlijke functies. De RSA cryptosysteem is het meest populaire public-key cryptosysteem sterkte van die is gebaseerd op de praktische moeilijkheid van het factoring van de zeer grote aantallen.,
-
Codering Functie − Het wordt beschouwd als een one-way functie van het omzetten van tekst in de cijfertekst en kan worden teruggenomen met de kennis van private sleutel d.
-
het Genereren van een Sleutel − De moeilijkheid van het bepalen van een eigen sleutel van een openbare RSA-sleutel is gelijk aan het factoriseren van de modulus n. Een aanvaller kan dus niet gebruik maken van de kennis van een RSA public-key om te bepalen van een RSA private key, tenzij hij kan een factor n. Het is ook een one-way functie, gaande van p & q waarden modulus n is eenvoudig maar het omgekeerde is niet mogelijk.,
als een van deze twee functies niet eenrichtingsverkeer blijkt te zijn, dan wordt RSA verbroken. In feite, als een techniek voor factoring efficiënt wordt ontwikkeld dan zal RSA niet meer veilig zijn.
de sterkte van RSA encryptie daalt drastisch tegen aanvallen als het getal p en q geen grote priemgetallen zijn en/ of gekozen publieke sleutel e een klein getal is.
ElGamal cryptosysteem
samen met RSA worden andere publieke-sleutel cryptosystemen voorgesteld. Veel van hen zijn gebaseerd op verschillende versies van het Discrete logaritme probleem.,
Elgamal cryptosysteem, elliptische Curve Variant genoemd, is gebaseerd op het Discrete logaritme probleem. Het ontleent de kracht uit de veronderstelling dat de discrete logaritmen niet kunnen worden gevonden in het praktische tijdsbestek voor een bepaald getal, terwijl de omgekeerde werking van de macht efficiënt kan worden berekend.
laten we een eenvoudige versie van ElGamal doornemen die werkt met getallen modulo p. in het geval van elliptische curvevarianten is deze gebaseerd op heel andere getallenstelsels.,
generatie van ElGamal sleutelpaar
elke gebruiker van Elgamal cryptosysteem genereert het sleutelpaar als volgt –
-
het kiezen van een groot priemgetal p. over het algemeen wordt een priemgetal van 1024 tot 2048 bits gekozen.
-
het kiezen van een generatorelement g.
-
Dit getal moet tussen 1 en p − 1 liggen, maar kan geen enkel getal zijn.
-
het is een generator van de multiplicatieve groep van gehele getallen modulo p. Dit betekent dat Voor elk geheel getal m co-priemgetal tot p, er een geheel getal k zodanig is dat gk = een mod n.,
bijvoorbeeld, 3 is generator van groep 5 (Z5 = {1, 2, 3, 4}).
-
| N | 3n | 3n mod 5 |
|---|---|---|
| 1 | 3 | 3 |
| 2 | 9 | 4 |
| 3 | 27 | 2 |
| 4 | 81 | 1 |
-
het Kiezen van de private sleutel. De private sleutel x is elk getal groter dan 1 en kleiner dan p-1.
-
computergedeelte van de publieke sleutel., De waarde y wordt als volgt berekend uit de parameters p, g en de private sleutel x −
y = gx mod p
-
het verkrijgen van publieke sleutel. De Elgamal publieke sleutel bestaat uit de drie parameters (p, g, y).
bijvoorbeeld, stel dat p = 17 en g = 6 (Het kan worden bevestigd dat 6 een generator is van groep Z17). De private sleutel x kan elk getal groter zijn dan 1 en kleiner dan 71, dus kiezen we x = 5. De waarde y wordt dan als volgt berekend –
y = 65 mod 17 = 7
-
dus de private sleutel is 62 en de publieke sleutel is (17, 6, 7).,
encryptie en decryptie
het genereren van een Elgamal sleutelpaar is relatief eenvoudiger dan het gelijkwaardige proces voor RSA. Maar de encryptie en decryptie zijn iets complexer dan RSA.
ElGamal encryptie
stel dat de afzender een platte tekst wil sturen naar iemand wiens ElGamal publieke sleutel is (p, G, y), Dan −
-
afzender vertegenwoordigt de platte tekst als een reeks getallen modulo p.
-
om de eerste platte tekst P te versleutelen, die wordt weergegeven als een getal modulo p., Het coderingsproces om de versleuteling C te verkrijgen is als volgt −
- willekeurig een getal k genereren;
- Bereken twee waarden C1 en C2, waarbij −
C1 = gk mod pC2 = (P*yk) mod p
-
stuur de versleuteling C, bestaande uit de twee afzonderlijke waarden (C1, C2), samen verzonden.,
-
verwijzend naar ons ElGamal key generation voorbeeld hierboven, wordt de platte tekst P = 13 als volgt versleuteld −
- willekeurig een getal genereren, zeg k = 10
- Bereken de twee waarden C1 en C2, waarbij −
C1 = 610 mod 17C2 = (13*710) mod 17 = 9
-
stuur de cijfertekst C = (C1, C2) = (15, 9).,
Elgamal decryptie
-
om de versleuteling (C1, C2) met behulp van private sleutel x te decoderen, worden de volgende twee stappen genomen −
-
Bereken de modulaire inverse van (C1)x modulo p, die (C1)-x is , in het algemeen aangeduid als decryptie factor.,
-
Verkrijg de platte tekst met behulp van de volgende formule −
-
C2 × (C1)-x mod p = Plaintext
-
in ons voorbeeld, om de versleuteling te decoderen C = (C1, C2) = (15, 9) met behulp van private sleutel x = 5, is de decryptie factor
15-5 mod 17 = 9
-
extract plaintext p = (9 × 9) mod 17 = 13.
Elgamal analyse
in ElGamal-systeem heeft elke gebruiker een private sleutel x. en heeft drie componenten van public key-prime modulus p, generator g, en public Y = GX mod p., De kracht van het ElGamal is gebaseerd op de moeilijkheid van discrete logaritme probleem.
de beveiligde sleutelgrootte is over het algemeen > 1024 bits. Vandaag zelfs 2048 bits lange sleutel worden gebruikt. Op het gebied van verwerkingssnelheid is Elgamal vrij traag, het wordt voornamelijk gebruikt voor sleutel authenticatie protocollen. Door de hogere verwerkingsefficiëntie worden elliptische Curvevarianten van ElGamal steeds populairder.,
Elliptic Curve Cryptography (ECC)
Elliptic Curve Cryptography (ECC) is een term die wordt gebruikt om een reeks cryptografische tools en protocollen te beschrijven waarvan de beveiliging is gebaseerd op speciale versies van het discrete logaritmeprobleem. Het Gebruikt geen getallen modulo p.
ECC is gebaseerd op verzamelingen van getallen die geassocieerd zijn met wiskundige objecten die elliptische krommen worden genoemd. Er zijn regels voor het optellen en berekenen van veelvouden van deze getallen, net zoals er zijn voor getallen modulo p.,
ECC bevat varianten van vele cryptografische schema ‘ s die oorspronkelijk ontworpen waren voor modulaire getallen zoals Elgamal encryptie en algoritme voor digitale handtekeningen.
aangenomen wordt dat het discrete logaritmeprobleem veel moeilijker is wanneer toegepast op punten op een elliptische kromme. Dit vraagt om het overschakelen van getallen modulo p naar punten op een elliptische kromme. Ook een gelijkwaardig veiligheidsniveau kan worden verkregen met kortere toetsen als we elliptische curve-gebaseerde varianten gebruiken.,
de kortere sleutels resulteren in twee voordelen-
- gemak van sleutelbeheer
- efficiënte berekening
deze voordelen maken elliptische-curve-gebaseerde varianten van encryptie-schema zeer aantrekkelijk voor toepassingen waar computerbronnen beperkt zijn.
RSA en ElGamal schema ‘s-een vergelijking
laten we kort de RSA en ElGamal schema’ s vergelijken op de verschillende aspecten.
| RSA | ElGamal | het is efficiënter voor encryptie. | het is efficiënter voor decryptie., |
|---|---|
| het is minder efficiënt voor decryptie. | het is efficiënter voor decryptie. |
| voor een bepaald beveiligingsniveau zijn lange sleutels vereist in RSA. | voor hetzelfde beveiligingsniveau zijn zeer korte sleutels vereist. |
| het wordt algemeen aanvaard en gebruikt. | het is nieuw en niet erg populair in de markt. |