kans
leerdoelstelling(en)
· definieer gebeurtenis, resultaat, proef, eenvoudige gebeurtenis, monsterruimte en bereken de kans dat een gebeurtenis zal plaatsvinden.
* Bereken de waarschijnlijkheid van gebeurtenissen voor complexere uitkomsten.
* toepassingen oplossen met waarschijnlijkheden.
Inleiding
waarschijnlijkheid geeft aan hoe waarschijnlijk het is dat er iets zal gebeuren., Het is een getal tussen en inclusief de getallen 0 en 1. Het kan worden geschreven als een breuk, een decimaal, of een procent.

willekeurig kiezen betekent dat er geen specifieke volgorde is waarin ze worden gekozen. Veel spellen gebruiken dobbelstenen of spinners om willekeurig nummers te genereren. Als je begrijpt hoe je kansen kunt berekenen, kun je doordachte beslissingen nemen over het spelen van deze spellen door de waarschijnlijkheid van verschillende uitkomsten te kennen.,
definities
eerst moet u een aantal termen met betrekking tot waarschijnlijkheid kennen. Bij het werken met waarschijnlijkheid wordt een willekeurige actie of reeks acties een proef genoemd. Een resultaat is het resultaat van een proef, en een gebeurtenis is een bepaalde verzameling van resultaten. Gebeurtenissen worden meestal beschreven met behulp van een gemeenschappelijk kenmerk van de uitkomsten.
laten we deze taal toepassen om te zien hoe de termen in de praktijk werken. Sommige spellen vereisen het rollen van een dobbelsteen met zes zijden, genummerd van 1 tot 6. (Dobbelstenen is het meervoud van dobbelsteen.,) De grafiek hieronder illustreert het gebruik van trial, outcome, en event voor een dergelijk spel:
merk op dat een verzameling van uitkomsten in accolades wordt gezet en gescheiden door komma ‘ s.
een eenvoudige gebeurtenis is een gebeurtenis met slechts één resultaat. Het rollen van een 1 zou een eenvoudige gebeurtenis zijn, want er is maar één resultaat dat werkt—1! Het rollen van meer dan een 5 zou ook een eenvoudige gebeurtenis, omdat het evenement bevat slechts 6 als een geldige uitkomst. Een samengestelde gebeurtenis is een gebeurtenis met meer dan één uitkomst. Bijvoorbeeld, bij het rollen van een zeszijdige matrijs, het rollen van een even aantal kan optreden met een van de drie uitkomsten: 2, 4 en 6.,
wanneer je een zeszijdige dobbelsteen vaak rolt, moet je niet verwachten dat een uitkomst vaker gebeurt dan een andere (aangenomen dat het een eerlijke dobbelsteen is). De resultaten in een situatie als deze zouden even waarschijnlijk zijn. Het is erg belangrijk om te herkennen wanneer de uitkomsten even waarschijnlijk zijn bij het berekenen van waarschijnlijkheid. Aangezien elke uitkomst in de die-rolling trial even waarschijnlijk is, zou je verwachten om elke uitkomst ![]() van de rollen te krijgen., Dat wil zeggen, je zou verwachten dat
van de rollen te krijgen., Dat wil zeggen, je zou verwachten dat ![]() van de rollen 1 is,
van de rollen 1 is, ![]() van de rollen 2,
van de rollen 2, ![]() van de rollen 3, enzovoort.
van de rollen 3, enzovoort.
een spinner is verdeeld in vier gelijke delen, elk gekleurd met een andere kleur zoals hieronder getoond. Wanneer deze spinner wordt gesponnen, wijst de pijl naar een van de kleuren. Zijn de resultaten even waarschijnlijk?
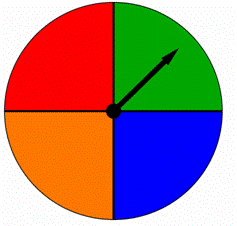
A) ja, ze zijn even waarschijnlijk.
B) Nee, ze zijn niet even waarschijnlijk.,
waarschijnlijkheid van gebeurtenissen
de waarschijnlijkheid van een gebeurtenis is hoe vaak deze verwacht wordt. Het is de verhouding tussen de grootte van de gebeurtenisruimte en de grootte van de monsterruimte.
eerst moet u de grootte van de monsterruimte bepalen. De grootte van de steekproefruimte is het totale aantal mogelijke resultaten. Als je bijvoorbeeld 1 matrijs rolt, is de monsterruimte 1, 2, 3, 4, 5, of 6. Dus de grootte van de monsterruimte is 6.
dan moet u de grootte van de gebeurtenisruimte bepalen., De evenementenruimte is het aantal resultaten in het evenement waarin u geïnteresseerd bent. De evenementenruimte voor het rollen van een nummer minder dan drie is 1 of 2. Dus de grootte van de gebeurtenisruimte is 2.
Voor even waarschijnlijke uitkomsten kan de waarschijnlijkheid van een gebeurtenis E worden geschreven P (E).
![]()
|
Example |
probleem |
een spel vereist het rollen van een zeszijdige die genummerd van 1 tot 6., Wat is de kans op het rollen van een even getal? |
|
Monster ruimte = {1, 2, 3, 4, 5, 6}
Gebeurtenis-ruimte = {2, 4, 6} |
ten Eerste, het vinden van het monster ruimte en de ruimte voor evenementen. De steekproefruimte is alle mogelijke uitkomsten, en de gebeurtenisruimte is de uitkomsten van de gebeurtenis. In dit geval, het evenement is “rollen een even aantal.,” |
|
|
|
Sinds de uitkomsten even waarschijnlijk zijn, de waarschijnlijkheid van de gebeurtenis is de verhouding van het evenement ruimte om te proeven van de ruimte., |
|
|
Antwoord |
P(even aantal) = |
|
Het is een algemene praktijk met kansen, als met breuken in het algemeen, te vereenvoudigen en een kans tot laagste waarde omdat dat het makkelijker maakt voor de meeste mensen om een idee te krijgen van hoe groot het is. Tenzij er reden is om dit niet te doen, alle uiteindelijke kansen in de laagste termen uit te drukken.,
een spinner is verdeeld in gelijke delen, elk gekleurd met een andere kleur zoals hieronder getoond., Vind de waarschijnlijkheid van het spinnen blauw of groen op deze spinner:
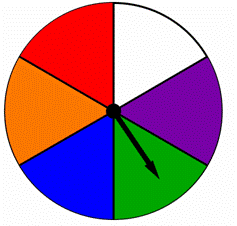
A) ![]()
B) ![]()
C) 2
D) 6
Tellen Methoden te vinden Steekproef Ruimten
Het moeilijkste wat er is voor de berekening van waarschijnlijkheid kan worden met het vinden van de omvang van de steekproef de ruimte, vooral als er twee of meer proeven. Er zijn verschillende telmethoden die kunnen helpen.,
de eerste om naar te kijken is het maken van een grafiek. In het onderstaande voorbeeld draait Tori twee munten. Dus je moet de monsterruimte zorgvuldig te bepalen. Een grafiek zoals die in het volgende voorbeeld wordt getoond is een goede benadering.
|
voorbeeld |
||||
|
probleem |
Tori slaat een paar munten om en noteert hoeveel keer “koppen” ze krijgt. Wat is de kans dat ze twee hoofden flipt?, Wat is de kans dat ze maar 1 hoofd flipt?,15ecf6″>T |
T |
TT |
|
sample space: {HH, HT, TH, TT}
event space for 2 heads: {HH}
event space for 1 head: {HT, TH}
Create a chart to record the results of flipping the first coin, followed by the result of flipping the second coin.,
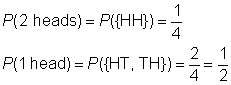
Sinds de uitkomsten even waarschijnlijk zijn, de waarschijnlijkheid van de gebeurtenis is de verhouding van het evenement ruimte om te proeven van de ruimte.,
Antwoord
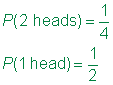
In het voorbeeld hieronder is het voorbeeld van ruimte voor Tori is zo simpel als alleen een dobbelsteen wordt gegooid. Echter, omdat James rolt twee sterven, een grafiek helpt om de informatie te organiseren.,
|
voorbeeld |
||||||||
|
probleem |
Tori rolde een zeszijdige matrijs en wilde een resultaat van 1 of 4. James gooide twee zeszijdige dobbelstenen, een blauwe en een rode, en wilde een resultaat van zowel een 1 en een 3 te krijgen, op hetzelfde moment. Welke gebeurtenis heeft een grotere kans?, |
|||||||
|
Tori’s sample space: {1, 2, 3, 4, 5, 6}
Tori’s event space: {1, 4}
Tori:
|
First, find the sample space and the event space for the two trials., Voor Tori ‘ s proces is dit eenvoudig. omdat de uitkomsten even waarschijnlijk zijn, is de waarschijnlijkheid van de gebeurtenis de verhouding tussen gebeurtenisruimte en monsterruimte.,316594724″> 6 |
6,1 |
6,2 |
6,3 |
6,4 |
6,5 |
6,6 |
|
James’ sample space has 36 outcomes.,
James’ gebeurtenisruimte heeft 2 uitkomsten.
Het is niet zo duidelijk voor James’ proef, omdat hij twee dobbelstenen gooit. Gebruik een grafiek om de mogelijkheden te vinden.
er zijn 36 Resultaten. Hiervan zijn er 2 die zowel 1 als 3 hebben.,
Jacobus: ![]()
Sinds de uitkomsten even waarschijnlijk zijn, de waarschijnlijkheid van de gebeurtenis is de verhouding van het evenement ruimte om te proeven van de ruimte.
antwoord
Tori ‘ s gebeurtenis heeft een grotere waarschijnlijkheid.,
u kunt ook een boomdiagram gebruiken om de monsterruimte te bepalen. Een boomdiagram heeft een tak voor elke mogelijke uitkomst voor elke gebeurtenis.stel dat een kast drie broeken heeft (zwart, wit en groen), Vier hemden (groen, wit, paars en geel) en twee paar schoenen (zwart en Wit). Hoeveel verschillende outfits kunnen worden gemaakt? Er zijn 3 keuzes voor broeken, 4 keuzes voor shirts, en 2 keuzes voor schoenen., Voor ons boomdiagram gebruiken we B Voor zwart, W voor wit, g voor groen, P voor paars en Y voor geel.
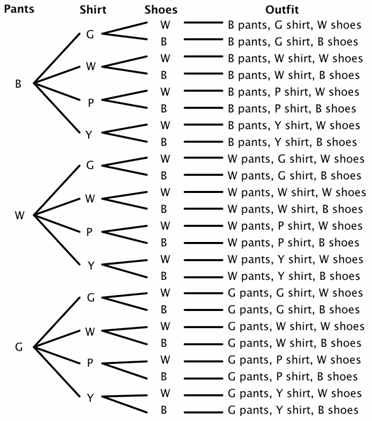
u kunt aan de hand van het boomdiagram zien dat er 24 mogelijke outfits (sommige misschien niet goede keuzes) in de steekproefruimte zijn.
nu kunt u vrij eenvoudig een aantal waarschijnlijkheidsproblemen oplossen. Wat is bijvoorbeeld de kans dat als je je ogen sluit en willekeurig kiest, je Broeken en schoenen met dezelfde kleur zou kiezen? Je kunt zien dat er 8 outfits zijn waar de broek en de schoenen bij passen.,
![]()
zoals u hebt gezien, hoeft u niet altijd elke uitkomst in de steekproefruimte te identificeren om een waarschijnlijkheid te berekenen. Je hebt alleen het aantal uitkomsten nodig.
Het fundamentele Tellingsprincipe is een manier om het aantal resultaten te vinden zonder ze allemaal op te sommen en te tellen.,
Het fundamentele Tellingsprincipe
als één gebeurtenis p mogelijke uitkomsten heeft en een andere gebeurtenis m mogelijke uitkomsten, dan zijn er in totaal p • m mogelijke uitkomsten voor de twee gebeurtenissen.
voorbeelden
· twee zeszijdige dobbelstenen rollen: elke dobbelsteen heeft 6 even waarschijnlijke uitkomsten, dus de steekproefruimte is 6 • 6 of 36 even waarschijnlijke uitkomsten.
* drie munten omgooien: elke munt heeft 2 even waarschijnlijke uitkomsten, dus de monsterruimte is 2 • 2 • 2 of 8 even waarschijnlijke uitkomsten.,
* een zeszijdige dobbelsteen rollen en een munt omgooien: de monsterruimte is 6 * 2 of 12 even waarschijnlijke uitkomsten.
dus je zou het fundamentele Telprincipe kunnen gebruiken om uit te vinden hoeveel outfits er zijn in het vorige voorbeeld. Er zijn 3 keuzes voor broeken, 4 keuzes voor shirts, en 2 keuzes voor schoenen. Met behulp van de fundamentele tellen principe, heb je 4 • 3 • 2 = 24 verschillende outfits.,
|
Voorbeeld |
||
|
Op. |
Barry vrijwilligers bij een goed doel wandeling te maken lunches voor alle andere vrijwilligers. In elke zak legt hij: · een van de twee sandwiches (pindakaas en gelei, of kalkoen en kaas), · een van de drie chips (gewone chips, gebakken chips of maïschips), · Een stuk fruit (een appel of een sinaasappel)., hij vergat te markeren wat er in de zakken zat. Ervan uitgaande dat elke keuze even waarschijnlijk is, wat is de kans dat de zak Therese krijgt een pindakaas en jam sandwich en een appel bevat?, |
|
|
Size of sample space:
(number of sandwich choices) • (number of chip choices) • (number of fruit choices) = 2 • 3 • 2 = 12
|
First, use the Fundamental Counting Principle to find the size of the sample space., |
|
|
Grootte van de ruimte:
(aantal sandwich keuzes in het geval) • (nummer van de chip keuzes in het geval) • (aantal vruchten keuzes in het geval) = |
Voor het evenement de ruimte, volgen hetzelfde principe. In dit geval is er slechts één sandwich en één stuk fruit van belang, maar een van de drie soorten chips zijn aanvaardbaar., |
|
|
antwoord |
|
Gebruik De ratio om de waarschijnlijkheid te vinden. |
Carrie flipt vier munten en telt het aantal staarten. Er zijn vier manieren om precies één staart te krijgen: HHHT, HHTH, HTHH, en THHH. Wat is de kans dat Carrie precies één staart krijgt?,
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Summary
Probability helps you understand random, unpredictable situations where multiple outcomes are possible., Het is een maat voor de waarschijnlijkheid van een gebeurtenis, en het hangt af van de verhouding tussen gebeurtenis en mogelijke uitkomsten, als al die uitkomsten even waarschijnlijk zijn.