correlationeel onderzoek: het zoeken naar relaties tussen variabelen
in tegenstelling tot beschrijvend onderzoek, dat voornamelijk is ontworpen om statische beelden te leveren, omvat correlationeel onderzoek het meten van twee of meer relevante variabelen en een beoordeling van de relatie tussen Of tussen deze variabelen., Bijvoorbeeld, de variabelen van lengte en gewicht zijn systematisch gerelateerd (gecorreleerd) omdat langere mensen over het algemeen meer wegen dan kortere mensen. Op dezelfde manier zijn studietijd-en geheugenfouten ook gerelateerd, omdat hoe meer tijd een persoon wordt gegeven om een lijst met woorden te bestuderen, hoe minder fouten hij of zij zal maken. Wanneer er twee variabelen in het onderzoeksontwerp zijn, wordt één van hen de voorspellende variabele genoemd en de andere de resultaatvariabele., Het ontwerp van het onderzoek kan worden gevisualiseerd als deze, waar de gebogen pijl geeft de verwachte correlatie tussen de twee variabelen:
Figuur 2.2.2

Een manier van organiseren van de gegevens van een correlational studie met twee variabelen is de grafiek van de waarden van elk van de gemeten variabelen door middel van een spreidingsdiagram. Zoals je kunt zien in Figuur 2.10 “voorbeelden van Scatter Plots”, een scatter plot is een visueel beeld van de relatie tussen twee variabelen., Voor elk individu wordt een punt uitgezet op het snijpunt van zijn of haar scores voor de twee variabelen. Wanneer de associatie tussen de variabelen op het verstrooiingsperceel gemakkelijk kan worden benaderd met een rechte lijn, zoals in de delen (A) en (b) van figuur 2.10 “voorbeelden van Verstrooiingspercelen”, wordt gezegd dat de variabelen een lineaire relatie hebben.
wanneer de rechte aangeeft dat individuen die bovengemiddelde waarden hebben voor een variabele ook bovengemiddelde waarden hebben voor de andere variabele, zoals in deel (a), wordt gezegd dat de relatie positief lineair is., Voorbeelden van positieve lineaire relaties zijn die tussen lengte en gewicht, tussen onderwijs en inkomen, en tussen leeftijd en wiskundige vaardigheden bij kinderen. In elk geval hebben mensen die hoger scoren op een van de variabelen ook de neiging om hoger te scoren op de andere variabele. Negatieve lineaire relaties daarentegen, zoals weergegeven in Deel (b), treden op wanneer bovengemiddelde waarden voor een variabele meestal geassocieerd worden met ondergemiddelde waarden voor de andere variabele., Voorbeelden van negatieve lineaire relaties zijn die tussen de leeftijd van een kind en het aantal luiers dat het kind gebruikt, en tussen oefenen op en fouten gemaakt op een leertaak. In deze gevallen hebben mensen die hoger scoren op een van de variabelen de neiging om lager te scoren op de andere variabele.
relaties tussen variabelen die niet met een rechte lijn kunnen worden beschreven, worden niet-lineaire relaties genoemd. Deel (c) van figuur 2.10 “voorbeelden van Spreidingspercelen” toont een gemeenschappelijk patroon waarin de verdeling van de punten in wezen willekeurig is., In dit geval is er helemaal geen relatie tussen de twee variabelen, en ze worden gezegd dat ze onafhankelijk zijn. In de delen d) en e) van figuur 2.10 “voorbeelden van Spreidingspercelen” worden associatiepatronen weergegeven waarin, hoewel er een associatie is, de punten niet goed worden beschreven door een enkele rechte. Bijvoorbeeld, deel (d) toont het type van relatie die vaak voorkomt tussen angst en prestaties., De verhogingen van bezorgdheid van lage tot gematigde niveaus worden geassocieerd met prestatiesverhogingen, terwijl de verhogingen van bezorgdheid van gematigde tot hoge niveaus met dalingen van prestaties worden geassocieerd. Relaties die van richting veranderen en dus niet door een enkele rechte worden beschreven, worden kromlijnige relaties genoemd.
figuur 2.10 voorbeelden van Scatter Plots
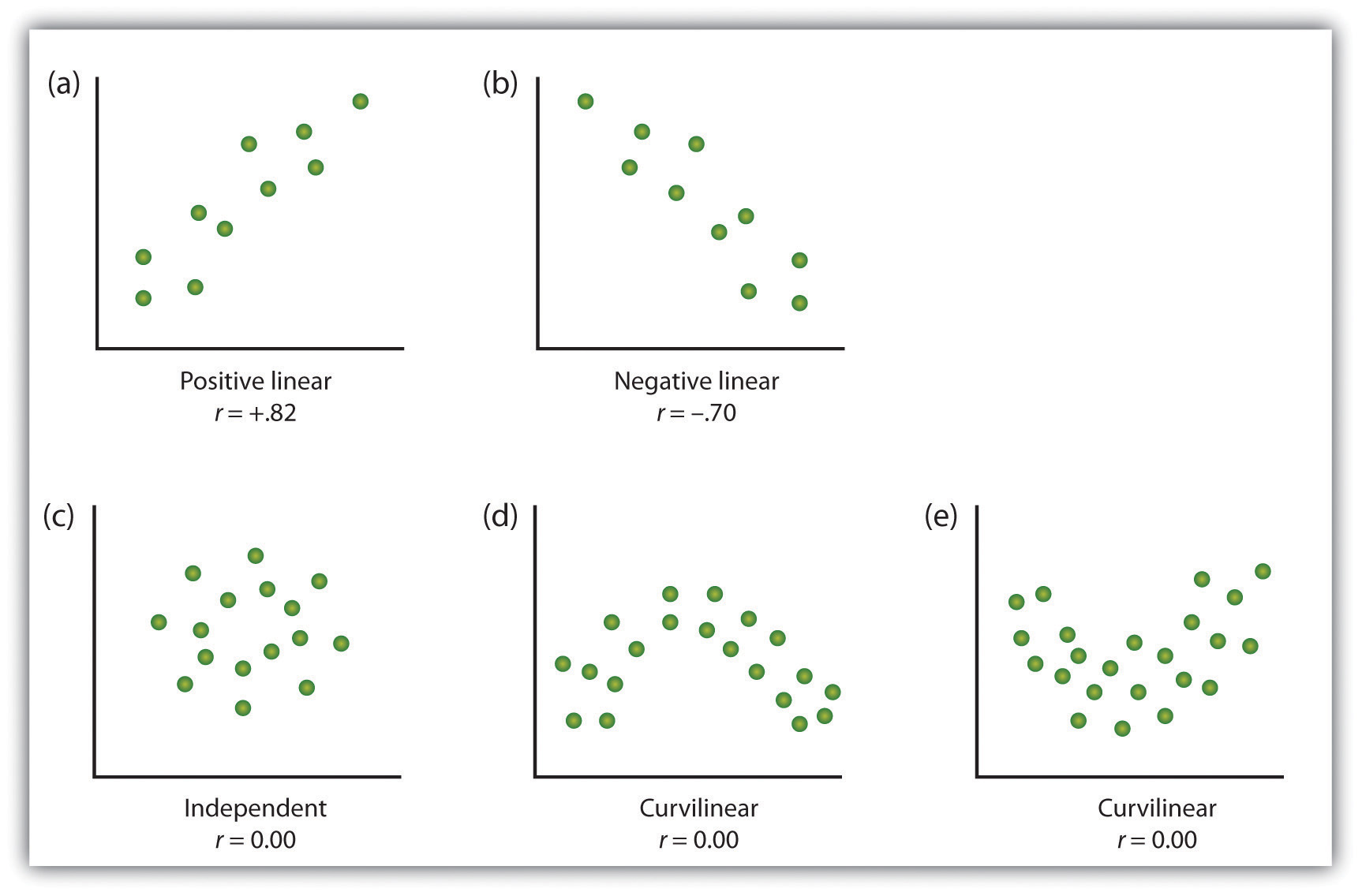
enkele voorbeelden van relaties tussen twee variabelen zoals weergegeven in scatter plots., Merk op dat de Pearson correlatiecoëfficiënt (r) tussen variabelen die kromlijnige relaties hebben waarschijnlijk dicht bij nul zal zijn.
aangepast aan Stangor, C. (2011). Onderzoeksmethoden voor de gedragswetenschappen (4th ed.). Mountain View, CA: Cengage.
de meest voorkomende statistische maat voor de sterkte van lineaire relaties tussen variabelen is de correlatiecoëfficiënt Pearson, die wordt gesymboliseerd door de letter r. de waarde van de correlatiecoëfficiënt varieert van r = -1.00 tot r = +1,00., De richting van de lineaire relatie wordt aangegeven door het teken van de correlatiecoëfficiënt. Positieve waarden van r (zoals r = .54 of r=.67) geven aan dat de relatie positief lineair is (dat wil zeggen, het patroon van de punten op de scatter plot loopt van linksonder naar rechtsboven), terwijl negatieve waarden van r (zoals r = –.30 of r = –.72) geven negatieve lineaire relaties aan (d.w.z., de stippen lopen van linksboven naar rechtsonder). De sterkte van de lineaire relatie wordt geïndexeerd door de afstand van de correlatiecoëfficiënt tot nul (de absolute waarde)., Bijvoorbeeld, r = –.54 is een sterkere relatie dan r = .30, en r = .72 is een sterkere relatie dan r = –.57. Omdat de Pearson correlatiecoëfficiënt alleen lineaire relaties meet, worden variabelen die kromlijnige relaties hebben niet goed beschreven door r, en de waargenomen correlatie zal dicht bij nul zijn.
Het is ook mogelijk om de relaties tussen meer dan twee maten tegelijk te bestuderen., Een onderzoeksopzet waarin meer dan één voorspellende variabele wordt gebruikt om een enkele resultaatvariabele te voorspellen, wordt geanalyseerd door middel van meervoudige regressie (Aiken & West, 1991). Meervoudige regressie is een statistische techniek, gebaseerd op correlatiecoëfficiënten tussen variabelen, die het mogelijk maakt het voorspellen van een enkele uitkomst variabele uit meer dan één predictor variabele. Bijvoorbeeld, figuur 2.11 “voorspelling van Job Performance van drie voorspellende variabelen” toont een meervoudige regressieanalyse waarin drie voorspellende variabelen worden gebruikt om een enkel resultaat te voorspellen., Het gebruik van multiple regression analysis toont een belangrijk voordeel van correlationele onderzoeksontwerpen—ze kunnen worden gebruikt om voorspellingen te doen over de waarschijnlijke score van een persoon op een uitkomstvariabele (bijvoorbeeld job performance) gebaseerd op kennis van andere variabelen.
figuur 2.11 voorspelling van Job Performance van drie voorspellende variabelen
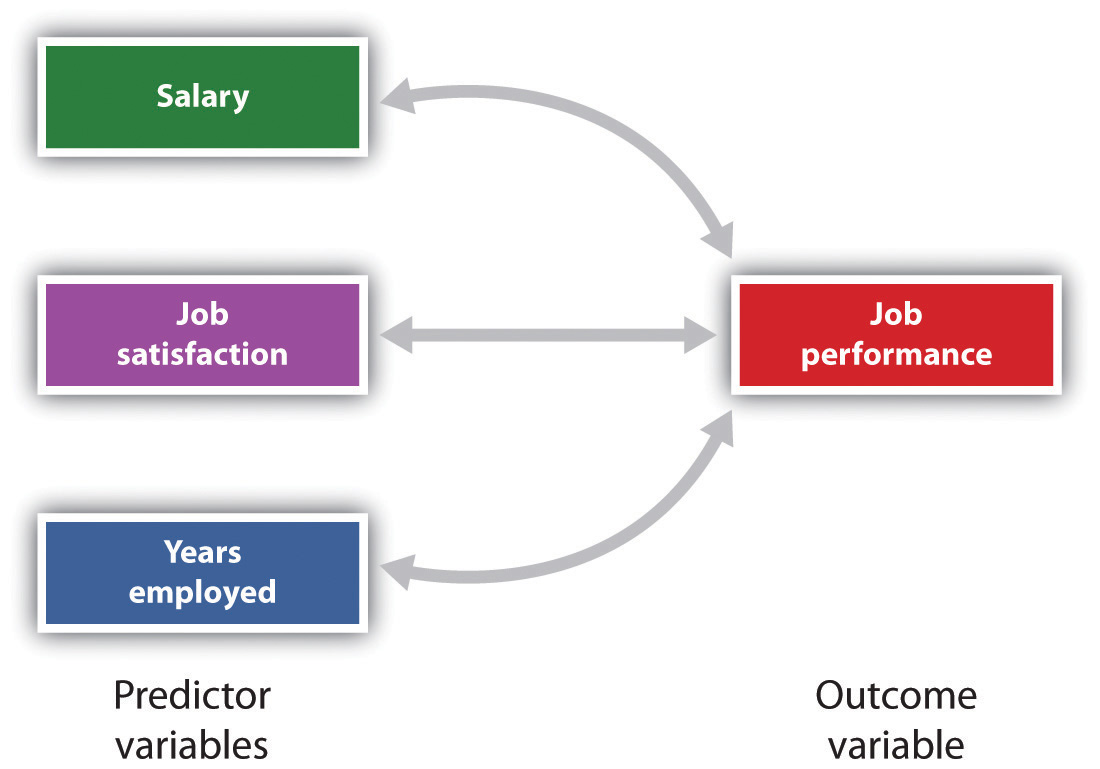
meervoudige regressie stelt wetenschappers in staat om de scores op een enkele uitkomstvariabele te voorspellen met behulp van meer dan één voorspellende variabele.,
een belangrijke beperking van correlationele onderzoeksontwerpen is dat ze niet kunnen worden gebruikt om conclusies te trekken over de causale relaties tussen de gemeten variabelen. Denk bijvoorbeeld aan een onderzoeker die heeft verondersteld dat het bekijken van gewelddadig gedrag zal leiden tot meer agressief spel bij kinderen. Hij heeft, uit een steekproef van kinderen uit de vierde klas, Een maat verzameld van het aantal gewelddadige televisieprogramma ‘ s dat elk kind tijdens de week bekijkt, evenals een maat van hoe agressief elk kind speelt op de schoolspeelplaats., Uit zijn verzamelde gegevens ontdekt de onderzoeker een positieve correlatie tussen de twee gemeten variabelen.
hoewel deze positieve correlatie de hypothese van de onderzoeker lijkt te ondersteunen, kan niet worden aangenomen dat het bekijken van gewelddadige televisie agressief gedrag veroorzaakt. Hoewel de onderzoeker geneigd is aan te nemen dat het bekijken van gewelddadige televisie agressief spel veroorzaakt, zijn er andere mogelijkheden
figuur 2.2.2

Er zijn andere mogelijkheden., Een alternatieve mogelijkheid is dat de causale richting precies het tegenovergestelde is van Wat is verondersteld. Misschien kinderen die gedroegen zich agressief op school ontwikkelen resterende opwinding die leidt hen naar wilt kijken naar gewelddadige tv-shows bij u thuis:
Figuur 2.2.2

Hoewel deze mogelijkheid lijkt minder waarschijnlijk, er is geen manier om uit te sluiten van de mogelijkheid van dergelijke omgekeerde causaliteit op basis van deze geconstateerde correlatie., Het is ook mogelijk dat beide causale richtingen werkt en dat de twee variabelen leiden tot elkaar:
Figuur 2.2.2

Nog een andere mogelijke verklaring voor de waargenomen correlatie is dat het geproduceerd is door de aanwezigheid van een common-causale variabele (ook bekend als een derde variabele)., Een algemeen-causale variabele is een variabele die geen deel uitmaakt van de onderzoekshypothese, maar die zowel de voorspeller als de resultaatvariabele veroorzaakt en dus de waargenomen correlatie tussen hen veroorzaakt. In ons voorbeeld is de disciplinestijl van de ouders van de kinderen een mogelijke veelvoorkomende causale variabele. Ouders die een harde en bestraffende discipline hanteren, kunnen kinderen voortbrengen die graag gewelddadige televisie kijken en zich agressief gedragen in vergelijking met kinderen waarvan de ouders minder strenge discipline hanteren:
figuur 2.2.,2
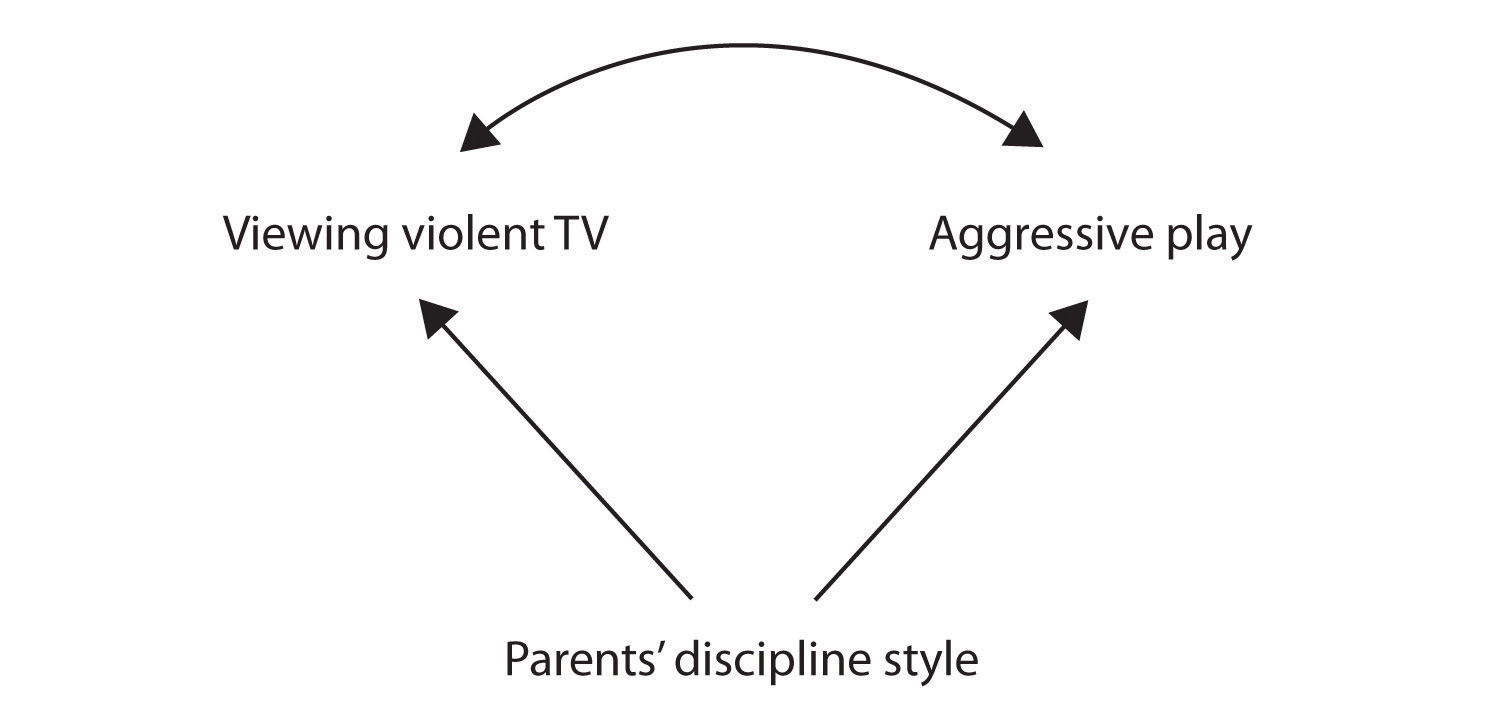
In dit geval zouden televisie kijken en agressief spel positief gecorreleerd zijn (zoals aangegeven door de gebogen pijl ertussen), hoewel geen van beide de oorzaak was van de andere, maar beide werden veroorzaakt door de discipline stijl van de ouders (de rechte pijlen). Wanneer de voorspeller en de outcome variabelen beide worden veroorzaakt door een common-causale variabele, wordt de waargenomen relatie tussen hen gezegd vals te zijn., Een onechte relatie is een relatie tussen twee variabelen waarin een algemeen-causale variabele de relatie produceert en “verklaart”. Als effecten van de common-causale variabele werden weggenomen, of gecontroleerd voor, de relatie tussen de voorspeller en uitkomst variabelen zou verdwijnen. In het voorbeeld kan de relatie tussen agressie en televisie kijken vals zijn omdat door het controleren van het effect van de disciplinerende stijl van de ouders, de relatie tussen televisie kijken en agressief gedrag zou kunnen verdwijnen.,
Common-causal variabelen in correlationele onderzoeksontwerpen kunnen worden beschouwd als” mysterie ” variabelen omdat, omdat ze niet zijn gemeten, hun aanwezigheid en identiteit zijn meestal onbekend voor de onderzoeker. Aangezien het niet mogelijk is om elke variabele te meten die zowel de voorspeller als de resultaatvariabelen kan veroorzaken, is het bestaan van een onbekende common-causal variabele altijd een mogelijkheid. Om deze reden blijven we over met de fundamentele beperking van correlatieonderzoek: correlatie toont geen oorzakelijk verband aan., Het is belangrijk dat wanneer je leest over correlationele onderzoeksprojecten, je rekening houdt met de mogelijkheid van valse relaties, en zorg ervoor dat de bevindingen correct te interpreteren. Hoewel correlatieonderzoek soms wordt gerapporteerd als het aantonen van causaliteit zonder enige vermelding van de mogelijkheid van omgekeerde causaliteit of gemeenschappelijke-causale variabelen, geïnformeerde consumenten van onderzoek, zoals u, zijn zich bewust van deze interpretatieproblemen.
kortom, correlatieontwerpen hebben zowel sterke punten als beperkingen., Eén kracht is dat ze kunnen worden gebruikt wanneer experimenteel onderzoek niet mogelijk is omdat de voorspellende variabelen niet kunnen worden gemanipuleerd. Correlatieontwerpen hebben ook het voordeel dat de onderzoeker gedrag kan bestuderen zoals het in het dagelijks leven voorkomt. En we kunnen ook correlatieontwerpen gebruiken om voorspellingen te doen—bijvoorbeeld om aan de hand van de scores op hun reeks tests het succes van jobstudenten tijdens een trainingssessie te voorspellen. Maar we kunnen dergelijke correlatiegegevens niet gebruiken om te bepalen of de opleiding tot betere prestaties op het werk heeft geleid. Daarvoor vertrouwen onderzoekers op experimenten.,