Sannsynligheten
læringsmål(s)
· Definere hendelsen, utfall, trial, enkelt hendelse, for eksempel plass og beregne sannsynligheten for at en hendelse vil inntreffe.
· Beregne sannsynligheten for hendelser for mer komplekse resultater.
· Løse programmer som involverer sannsynligheter.
Innledning
Sannsynlighet gir et mål på hvor sannsynlig det er at noe vil skje., Det er et tall mellom og inkluderer tallene 0 og 1. Det kan skrives som en brøk, til en desimal, eller en prosent.

Plukke tall tilfeldig betyr at det er ingen bestemt rekkefølge de er valgt. Mange spill bruker terninger eller spinnere til å generere tall tilfeldig. Hvis du forstår hvordan du skal beregne sannsynligheter, kan du gjøre gjennomtenkte beslutninger om hvordan å spille disse spillene ved å vite sannsynligheten for ulike utfall.,
Definisjoner
Første du trenger å vite noen vilkår knyttet til sannsynlighet. Når du arbeider med sannsynlighet, en tilfeldig handling eller en rekke handlinger som er kalt en rettssak. Et resultat som er resultatet av en rettssak, og en hendelse er en bestemt samling av resultater. Hendelser er vanligvis beskrevet ved hjelp av et felles kjennetegn for resultater.
La oss bruke dette språket for å se hvordan vilkårene fungerer i praksis. Noen spill krever at du kaster en terning med seks sider, nummerert fra 1 til 6. (Terning er flertall av dør.,) Diagrammet nedenfor illustrerer bruken av prøveversjon, utfall, og arrangement for slike spill:
legg Merke til at en samling av resultater er sett i bukseseler og adskilt med komma.
En enkel hendelse er en hendelse med bare ett resultat. Kaster en 1 ville være en enkel hendelse, fordi det er bare ett resultat som fungerer—1! Rolling mer enn en 5 vil også være en enkelt hendelse, fordi arrangementet har kun 6 som et gyldig resultat. En sammensatt hendelse er en hendelse med mer enn ett resultat. For eksempel, i ruller en seks-kantede terningen, rullende et partall kunne oppstå med en av tre mulige utfall: 2, 4, og 6.,
Når du ruller en seks-kantede terningen for mange ganger, bør du ikke forvente noen utfallet skal skje oftere enn en annen (forutsatt at det er en virkelig dø). Resultatene i en situasjon som dette er sagt å være like sannsynlige. Det er svært viktig å kjenne igjen når utfallene er like sannsynlige ved beregning av sannsynlighet. Siden hvert utfall i dør-rullende rettssaken er like sannsynlige, du ville forvente å få hvert utfall ![]() av ruller., Det vil si at du ville forvente
av ruller., Det vil si at du ville forvente ![]() av rolls til å være 1,
av rolls til å være 1, ![]() av rolls til å være 2,
av rolls til å være 2, ![]() av rolls å være 3, og så videre.
av rolls å være 3, og så videre.
Et hjul er delt inn i fire like deler, hver farget med en annen farge som vist under. Når dette hjulet er spunnet, peker pilen til en av fargene. Er resultatene like sannsynlige?
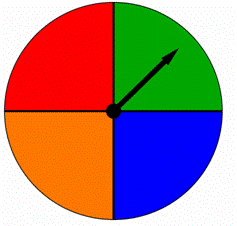
A) Ja, de er like sannsynlige.
B) Nei, de er ikke like sannsynlig.,
Sannsynligheten for Hendelser
sannsynligheten for en hendelse er hvor ofte det er forventet å oppstå. Det er forholdet mellom størrelsen på arrangementet plass til størrelsen på prøven plass.
Først, du trenger for å bestemme størrelsen på prøven plass. Størrelsen på utvalget plass er det totale antall mulige utfall. For eksempel, når du ruller 1 dør, prøve-plass 1, 2, 3, 4, 5, eller 6. Så størrelsen på prøven plass 6.
Så du trenger for å bestemme størrelsen på arrangementet plass., Arrangementet plass er antall utfall i tilfelle du er interessert i. Arrangementet plass for å kaste et nummer mindre enn tre er 1 eller 2. Så størrelsen på arrangementet plass er 2.
For like sannsynlig utfall, er sannsynligheten for en hendelse E kan skrives P(E).
![]()
|
Eksempel |
||
|
Problemet |
Et spill som krever at du kaster en seks-kantede terningen nummerert fra 1 til 6., Hva er sannsynligheten for å rulle et partall? |
|
|
Eksempel på plass = {1, 2, 3, 4, 5, 6}
Event plass = {2, 4, 6} |
Først må du finne eksempel på plass og tilstelninger. Prøven plass er alle mulige utfall, og arrangementet plass er resultatene i arrangementet. I dette tilfellet, vil hendelsen «rullende et partall.,» |
|
|
|
Siden utfall er like sannsynlige, sannsynligheten for hendelsen er forholdet mellom event plass til å smake på plass., |
|
|
Svar |
P(partall) = |
|
Det er en vanlig praksis med sannsynligheter, som med fraksjoner generelt, for å forenkle en sannsynlighet til laveste vilkårene siden som gjør det enklere for folk flest å få en følelse av hvor bra det er. Med mindre det er grunn til ikke å gjøre det, uttrykke alle endelige sannsynligheter i laveste vilkår.,
Et hjul er delt i to like deler, hver farget med en annen farge som vist under., Finn sannsynligheten for å spinne blå eller grønn på dette spinner:
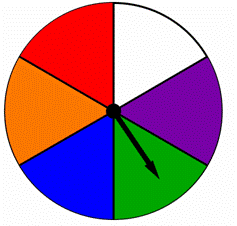
A) ![]()
B) ![]()
C) 2
D) 6
Telle Metoder for å finne Eksempel Mellomrom
Det aller vanskeligste for å beregne en sannsynlighet kan være å finne størrelsen på prøven plass, spesielt hvis det er to eller flere studier. Det er flere telle metoder som kan hjelpe.,
Den første til å se på er å lage et diagram. I eksempelet nedenfor, Tori er flipping to mynter. Så må du bestemme eksempel på plass nøye. Et diagram som vist i eksemplet som følger er en god tilnærming.
|
Eksempel |
||||
|
Problemet |
Tori er bla et par mynter og merke seg hvor mange knipser av «hoder» hun får. Hva er sannsynligheten for at hun knipser 2 hoder?, Hva er sannsynligheten for at hun knipser bare 1 hodet?,15ecf6″>T |
T |
TT |
|
sample space: {HH, HT, TH, TT}
event space for 2 heads: {HH}
event space for 1 head: {HT, TH}
Create a chart to record the results of flipping the first coin, followed by the result of flipping the second coin.,
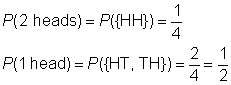
Siden utfall er like sannsynlige, sannsynligheten for hendelsen er forholdet mellom event plass til å smake på plass.,
Svar
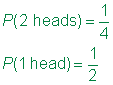
I eksemplet nedenfor eksempel plass for Tori er enkelt som bare én dør er å bli kastet. Imidlertid, siden James er rullende to die, et diagram hjelper til å organisere informasjon.,
|
Eksempel |
||||||||
|
Problemet |
Tori rullet en seks-kantede terningen, og ønsket å få et resultat av enten 1 eller 4. James rullet to seks-sidede terninger, en blå og en rød, og ønsket å få et resultat av både 1 og 3, på samme tid. Hvilken hendelse har en større sannsynlighet?, |
|||||||
|
Tori’s sample space: {1, 2, 3, 4, 5, 6}
Tori’s event space: {1, 4}
Tori:
|
First, find the sample space and the event space for the two trials., For Tori er prøving, er dette enkelt. Siden utfall er like sannsynlige, sannsynligheten for hendelsen er forholdet mellom event plass til å smake på plass.,316594724″> 6 |
6,1 |
6,2 |
6,3 |
6,4 |
6,5 |
6,6 |
|
James’ sample space has 36 outcomes.,
James’ arrangement plass har 2 utfall.
Det er ikke så åpenbart for James’ rettssaken, siden han kaster to terninger. Bruk kartet til å finne mulighetene.
Det er 36 resultater. Av disse er det 2 som har både 1 og 3.,
James: ![]()
Siden utfall er like sannsynlige, sannsynligheten for hendelsen er forholdet mellom event plass til å smake på plass.
Svar
Tori arrangementet har en større sannsynlighet.,
Du kan også bruke et tre-diagram for å bestemme eksempel på plass. Et tre-diagram har en filial for alle mulige utfall for hver hendelse.
la oss Anta at en skapet har tre par bukser (svart, hvit, og grønn), fire skjorter (grønn, hvit, lilla og gul), og to par sko (svart og hvit). Hvor mange forskjellige antrekk kan gjøres? Det er 3 alternativer for bukser, 4 valg for skjorter, og 2 valg for sko., For våre tre diagram, la oss bruke B for svart, W for hvite, G i grønt, P for lilla, og Y for gul.
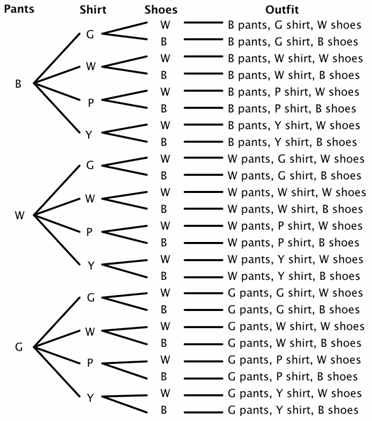
Du kan se fra treet diagrammet at det er 24 mulige antrekk (noen kanskje ikke stort valg) i prøven plass.
Nå kan du ganske enkelt løse noen sannsynlighet for problemer. For eksempel, hva er sannsynligheten for at hvis du lukker øynene og velge tilfeldig ville du velge bukser og sko med samme farge? Du kan se at det er 8 antrekk der bukser og sko kampen.,
![]()
Som du har sett, når en rettssak innebærer mer enn en tilfeldig element, for eksempel flipping mer enn én mynt eller rulle mer enn én dør, du er ikke alltid nødvendig å identifisere hvert utfall i utvalget plass til å beregne en sannsynlighet. Du trenger bare antallet resultater.
Den Grunnleggende Telle Prinsippet er en måte å finne antall utfall uten oppføringen og telle hver og en av dem.,
Det Grunnleggende Prinsippet Telle
Hvis en hendelse har p mulige utfall, og en annen hendelse som har m mulige utfall, da det er en total av p • m mulige utfall for de to hendelsene.
Eksempler
· Rullende to seks-sidede terninger: Hver dør har 6 like sannsynlige utfall, slik at prøven plass 6 • 6 eller 36 er like sannsynlige utfall.
· Flipping tre mynter: Hver mynt har 2 like sannsynlige utfall, slik at prøven plass 2 • 2 • 2 eller 8 like sannsynlige utfall.,
· Rolling en seks-kantede terningen og å snu en mynt: utvalget plass 6 • 2 eller 12 like sannsynlige utfall.
Slik at du kan bruke de Grunnleggende Telle Prinsippet for å finne ut hvor mange drakter er det i forrige eksempel. Det er 3 alternativer for bukser, 4 valg for skjorter, og 2 valg for sko. Bruke Grunnleggende Prinsippet Telle, du har 4 • 3 • 2 = 24 forskjellige antrekk.,
|
Eksempel |
||
|
Problemet |
Barry frivillige på en veldedig spasertur til å lage matpakker til alle de andre frivillige. I hver pose han setter: · en av to smørbrød (peanut smør og gelé, eller tyrkia og ost), · en av tre sjetonger (vanlig potet chips, bakt potet chips, eller mais chips), · ett stykke frukt (et eple eller en appelsin)., Han glemte å markere hva som var i bagene. Vi antar at hvert valg er like sannsynlige, hva er sannsynligheten for at posen Therese får har en peanut smør og gelé sandwich og en apple?, |
|
|
Size of sample space:
(number of sandwich choices) • (number of chip choices) • (number of fruit choices) = 2 • 3 • 2 = 12
|
First, use the Fundamental Counting Principle to find the size of the sample space., |
|
|
Størrelse på arrangementet plass:
(antall sandwich valg i tilfelle) • (antall chip valg i hendelse) • (antall frukt valg i hendelsen) = |
For tilstelninger, følger samme prinsipp. I dette tilfellet, det er bare en sandwich og et stykke frukt av interesse, men noen av de tre typer chips er akseptabelt., |
|
|
Svar |
|
Bruk-forholdet for å finne sannsynligheten. |
Carrie knipser fire mynter og teller antall mynt. Det er fire måter å få nøyaktig én hale: HHHT, HHTH, HTHH, og THHH. Hva er sannsynligheten for at Carrie blir nøyaktig én hale?,
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Summary
Probability helps you understand random, unpredictable situations where multiple outcomes are possible., Det er et mål på sannsynligheten for en hendelse, og det avhenger av forholdet mellom hendelse og mulige utfall, hvis alle disse utfallene er like sannsynlige.