for Å bruke den som referanse vinkel kalkulator, kan du ganske enkelt skrive inn en hvilken som helst vinkel til vinkel-boksen til å finne sin referanse vinkel, noe som er akutt vinkel som tilsvarer vinkelen inn. Kalkulatoren automatisk gjelder reglene vi ser nærmere på nedenfor.
Hva er en Referanse Vinkel, likevel?
Tenk deg et koordinere plan. La oss si at vi ønsker å tegne en vinkel som er 144° på vår planet., Vi starter på høyre side av x-aksen, der tre o ‘ clock er på en klokke. Vi roter mot klokken, som starter ved å gå opp. Vi fortsetter forbi 90° tilgangspunktet (den øverste delen av y-aksen) inntil vi får til 144°. Vi trekker en stråle fra opprinnelse, som er sentrum av flyet, til det punktet. Nå har vi en stråle som vi kaller terminal side. Men vi må trekke en mer ray til å gjøre en vinkel. Vi har et valg på dette punktet. Vårt andre ray behov for å være på x-aksen. Hvis vi trekker det fra opprinnelse til høyre, har vi trukket en vinkel som måler 144°., Hvis vi trekker den til venstre, har vi trukket en vinkel som måler 36°. Denne andre vinkel er referansen vinkel. Det er alltid den minste av de to vinkler, alltid vil være mindre enn eller lik 90°, og det vil alltid være positiv. Her er en animasjon som viser en referanse vinkel for fire ulike vinkler, som hver er i en annen kvadrant. Legg merke til hvordan andre ray er alltid på x-aksen.
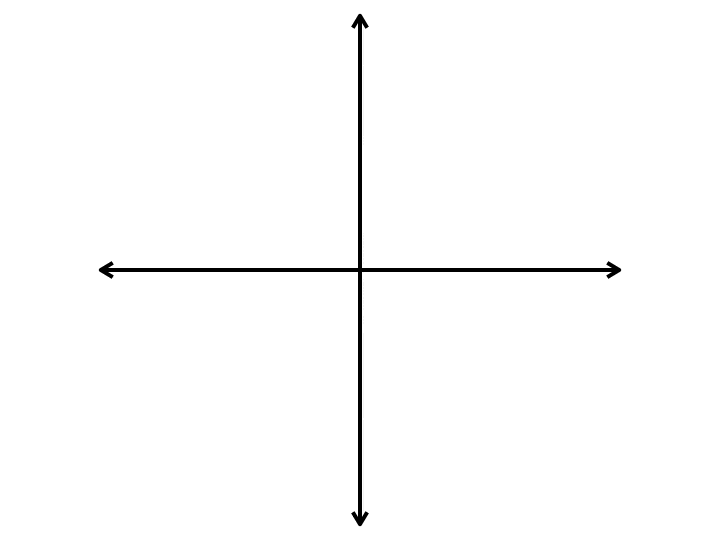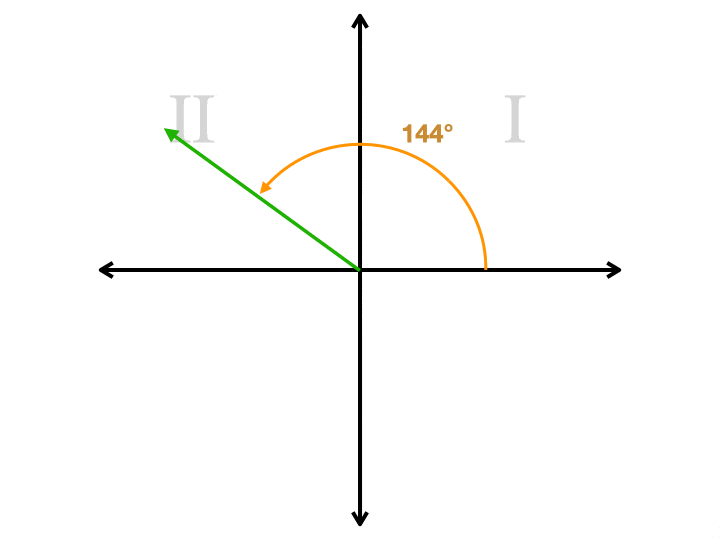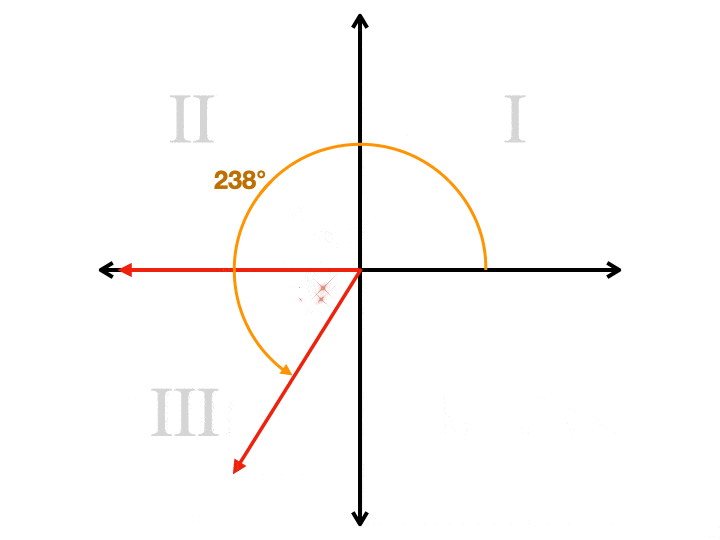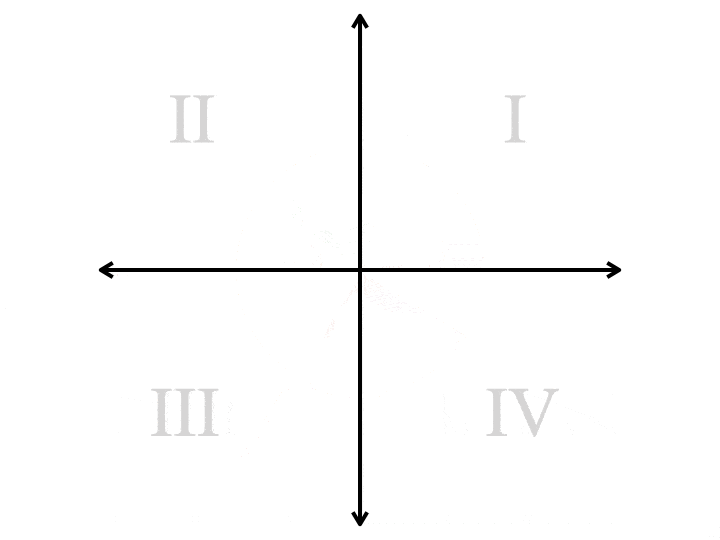
Hvor er Referansen Vinkel Nyttig?
referanse vinkel alltid har den samme trigonometriske funksjonen verdier som den opprinnelige vinkelen. Legg merke til at ordet verdier der., Skiltet kan ikke være det samme, men verdien vil alltid være det. Dette er nyttig for vanlige vinkler som 45° og 60°, som vi vil møte igjen og igjen. Når vi vet at deres sinus, cosinus og tangens verdier, vet vi også at verdiene for enhver vinkel som referanse vinkel er også 45° og 60°. Som for tegn, husk at Sinus er positiv i 1. og 2. kvadrant og Cosinus er positiv i 1. og 4. kvadrant.
Hvordan kan Vi Finne Referanse Vinkel uten Kalkulator?
Hvordan kan vi finne referanse vinkelen avhenger av kvadranten av terminalen side.,
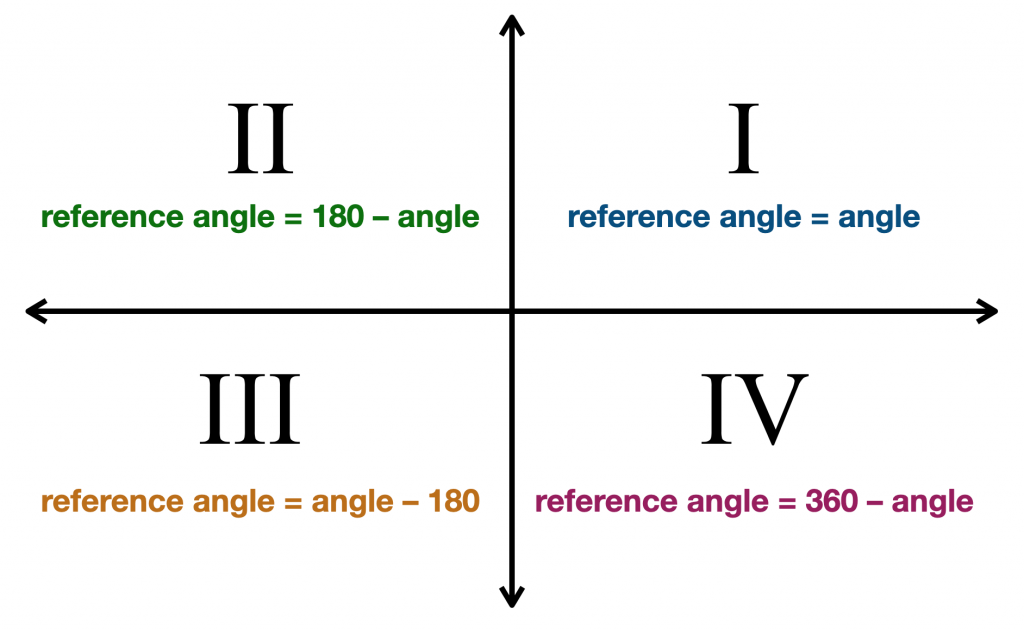
Når terminalen side er i første kvadrant (vinkler fra 0° til 90°), vår referanse vinkel er den samme som vår er gitt vinkel. Dette gir mening, siden alle vinkler i første kvadrant er mindre enn 90°. Så, hvis vår er gitt vinkel er 33°, deretter sin referanse vinkel er også 33°.
Når terminalen side er i andre kvadrant (vinkler fra 90° til 180°), vår referanse vinkel på 180° minus vår er gitt vinkel. Så, hvis vår er gitt vinkel er 110°, deretter sin referanse vinkel på 180° – 110° = 70°.,
Når terminalen side er i tredje kvadrant (vinkler fra 180° og 270°), vår referanse vinkel er vår gitt vinkel minus 180°. Så, hvis vår er gitt vinkel er 214°, deretter sin referanse vinkel er 214° – 180° = 34°.
Når terminalen side er i fjerde kvadrant (vinkler fra 270° til 360°), vår referanse vinkel er 360° minus vår er gitt vinkel. Så, hvis vår er gitt vinkel er 332°, deretter sin referanse vinkel er 360° – 332° = 28°.
Hva om Vår Vinkelen er Større enn 360°?,
Når en vinkel som er større enn 360°, som betyr at den har roteres helt rundt koordinere plan-og holdt på å gå. For å finne sin referanse vinkel, vi må først finne tilsvarende vinkel mellom 0° og 360°. Dette er lett å gjøre. Vi bare fortsette å trekke 360 fra det før det er nedenfor 360. For eksempel, hvis vår vinkel er 544°, vil vi trekke fra 360° fra den for å få 184° (544° – 360° = 184°). Nå ville vi merke til at det er i tredje kvadrant, så vi vil trekke fra 180° fra det å finne at vår referanse vinkel er 4°.
Hva om Vår Vinkel er Negativ?,
Når en vinkel som er negativt, vi flytter den andre retningen for å finne vår terminal side. Dette betyr at vi flytter med klokken i stedet for mot klokken når du tegner den. Eller vi kan beregne den ved bare å legge det til 360°. For eksempel, hvis vår er gitt vinkel er -110°, så vil vi legge det til 360° for å finne våre positive vinkel 250° (-110° + 360° = 250°). Nå ville vi ha å se at vi i tredje kvadrant, og gjelder som regel for å finne vår referanse vinkel (250° – 180° = 70°).