Offentlig Nøkkel Kryptografi
i Motsetning til symmetrisk kryptografi, vi finner ikke historisk bruk av offentlig-nøkkel kryptografi. Det er et relativt nytt konsept.
Symmetrisk kryptografi var godt egnet for organisasjoner som for eksempel myndigheter, militære, og store finansielle foretak var involvert i klassifisert kommunikasjon.,
Med spredningen av mer usikkert datamaskin-nettverk i siste tiårene, et reelt behov ble ansett å bruke kryptering på større skala. Den symmetriske nøkkelen ble funnet å være ikke-praktisk på grunn av utfordringer det står overfor for key management. Dette ga opphav til den offentlige nøkkelen cryptosystems.
prosessen med kryptering og dekryptering er vist i følgende illustrasjon −
– >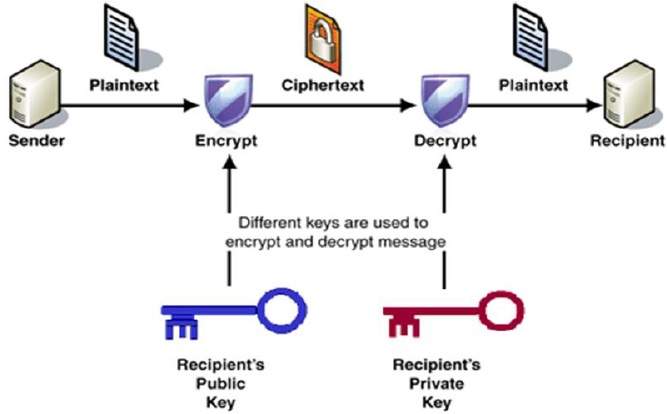
De viktigste egenskapene til offentlig nøkkel kryptering ordningen er −
– >
-
Forskjellige tastene brukes til kryptering og dekryptering., Dette er en egenskap som sett denne ordningen annerledes enn symmetrisk kryptering ordningen.
-
Hver mottaker besitter en unik dekrypteringsnøkkelen, vanligvis referert til som sin private nøkkel.
-
Mottakeren har behov for å publisere en krypteringsnøkkel, referert til som hans offentlige nøkkel.
-
Noen kvalitetssikring av ektheten av en offentlig nøkkel er nødvendig i denne ordningen for å unngå forfalskning av motstanderen som mottaker. Generelt, denne type nøkkel innebærer pålitelig tredjepart som bekrefter at en bestemt offentlig nøkkel tilhører en bestemt person eller enhet bare.,
-
krypteringsalgoritme som er komplekse nok til å forby angriper fra deducing ren tekst fra ciphertext og kryptering (offentlig) – tasten.
-
selv Om private og offentlige nøkler er i slekt matematisk, det er ikke mulig å beregne den private nøkkelen fra den offentlige nøkkelen. Faktisk, intelligent del av et offentlig-nøkkel nøkkel er å utforme et forhold mellom to nøkler.
Det er tre typer Offentlig Nøkkel Kryptering ordninger., Vi diskuterer dem i følgende seksjoner −
– >
RSA-Nøkkel
Denne nøkkel er en av de første system. Det er fortsatt mest ansatt nøkkel selv i dag. Systemet ble oppfunnet av tre forskere Ron Rivest, Adi Shamir og Len Adleman og det er derfor betegnet som RSA-nøkkel.
Vi vil se to sider av RSA-nøkkel, for det første generering av nøkkelpar og for det andre kryptering dekryptering algoritmer.,
Generasjon av RSA-nøkkelpar
Hver person eller et parti som ønsker å delta i kommunikasjon ved hjelp av kryptering behov for å generere et par nøkler, nemlig offentlig nøkkel og en privat nøkkel. Den prosessen som følges i generering av nøkler er beskrevet nedenfor −
– >
-
Generere RSA modulus (n)
-
Velg to store primtall p og q.
-
Beregne n=p*q. For sterk uknuselige kryptering, la n være et stort antall, vanligvis et minimum 512 bits.,
-
-
Finn Avledet Antall (e)
-
Antall e må være større enn 1 og mindre enn (p − 1)(q − 1).
-
Det må være noen felles faktor for e og (p − 1)(q − 1) med unntak for 1. Med andre ord to tall e og (p – 1)(q – 1) er coprime.
-
-
Form den offentlige nøkkelen
-
Det par av tall (n, e) form RSA offentlig nøkkel og er gjort offentlig.,
-
det er Interessant, selv om n er en del av den offentlige nøkkelen, problemer i factorizing et stort primtall sikrer at angriperen ikke kan finne i endelig tid de to primtall (p & q) brukes for å oppnå n. Dette er styrken av RSA.
-
-
Generere den private nøkkelen
-
Privat Nøkkel d er beregnet ut fra p, q og e. For en gitt n og e, det er unikt nummer d.
-
Antall d er den inverse av e modulus (p – 1)(q – 1)., Dette betyr at d er antall mindre enn (p – 1)(q – 1) slik at når multiplisert med e, det er lik 1 modulo (p – 1)(q – 1).
-
Dette forholdet er skrevet matematisk som følger −
– >
-
ed = 1 mod (p − 1)(q − 1)
Den Utvidede Euclidean Algoritmen tar p, q og e som input og gir d som output.
Eksempel
Et eksempel på generering av RSA-nøkkelpar er gitt nedenfor. (For enkel forståelse, primtall p & q tatt her er små verdier. Praktisk talt, er disse verdiene er meget høy).,
-
La to primtall p = 7 og q = 13. Dermed, modulus n = pq = 7 x 13 = 91.
-
Velg e = 5, som er et gyldig valg siden det er ingen tall som er felles faktor på 5 og (p − 1)(q− 1) = 6 × 12 = 72, bortsett fra 1.
-
Det par av tall (n, e) = (91, 5) danner offentlig nøkkel og kan gjøres tilgjengelig til alle som vi ønsker å være i stand til å sende oss krypterte meldinger.
-
Inngang p = 7, q = 13, og e = 5 til Utvidet Euclidean Algoritme. Produksjonen vil være d = 29.,
-
Sjekk at d beregnet er riktige ved computing −
– >
de = 29 × 5 = 145 = 1 mod 72
-
Derfor, offentlig nøkkel (91, 5) og private nøkler er (91, 29).
Kryptering og Dekryptering
Når nøkkelpar genereres, prosessen med kryptering og dekryptering er relativt enkel og beregninger enkle.
det er Interessant, RSA ikke opererer direkte på strenger av biter som i tilfelle av symmetrisk nøkkel kryptering. Den opererer på tall modulo n. Det er derfor nødvendig å representere ren tekst som en serie av tall mindre enn n.,
RSA-Kryptering
-
la oss Anta at avsender ønsker å sende en tekstmelding til noen som offentlig nøkkel er (n, e).
-
avsenderen så representerer ren tekst som en serie av tall mindre enn n.
-
for Å kryptere den første klartekst S, som er et tall modulo n. Selve prosessen er enkel matematisk trinn som −
– >
C = Pe mod n
-
med andre ord, ciphertext C er lik ren tekst P multiplisert med seg selv e ganger, og deretter redusert modulo n. Dette betyr at C er også et tall mindre enn n.,
-
Tilbake til vår Nøkkel Generasjon eksempel med ren tekst P = 10, får vi ciphertext C −
– >
C = 105 mod 91
RSA Dekryptering
-
dekryptering prosessen for RSA er også veldig grei. Anta at mottakeren av offentlig-nøkkel-par (n, e) har mottatt en ciphertext C.
-
– Mottaker reiser C kraft av sin private nøkkel d. Resultatet modulo n vil være ren tekst S.,
Plaintext = Cd mod n
-
Tilbake igjen til vårt numerisk eksempel den ciphertext C = 82 ville få dekryptert til nummer 10 bruk av privat nøkkel 29 −
– >
Plaintext = 8229 mod 91 = 10
RSA Analyse
sikkerheten i RSA, avhenger av styrken av to separate funksjoner. RSA-nøkkel er mest populære offentlig-nøkkel nøkkel styrke som er basert på praktiske problemer av factoring veldig stort tall.,
-
Kryptering Funksjon − Det er ansett som en en-veis funksjonen til å konvertere ren tekst i ciphertext og det kan reverseres bare med kunnskap av privat nøkkel d.
-
nøkkelgenerering − vanskeligheten av å bestemme en privat nøkkel fra en RSA offentlig nøkkel er tilsvarende til factoring den modulus n. En angriper kan dermed ikke bruke kunnskap om en RSA offentlig nøkkel til å finne en RSA private nøkkelen, med mindre han kan faktor n. Det er også en måte funksjon, som går fra p & q-verdier for å modulus n er enkelt, men bakover er ikke mulig.,
Hvis en av disse to funksjonene er vist ikke bare én vei, så RSA vil bli brutt. Faktisk, hvis en teknikk for factoring effektivt er utviklet RSA vil ikke lenger være trygge.
styrken av RSA-kryptering går drastisk ned mot angrep hvis nummeret p og q er ikke store primtall og/ eller valgt offentlig nøkkel e er et lite antall.
ElGamal Nøkkel
Sammen med RSA, det er andre offentlig-nøkkel cryptosystems foreslått. Mange av dem er basert på ulike versjoner av den Diskrete Logaritmen Problem.,
ElGamal nøkkel, kalt Elliptic Curve Variant, er basert på Diskrete Logaritmen Problem. Det får styrke fra den forutsetning at den diskrete logaritmer kan ikke bli funnet i praktisk tidsramme for et gitt antall, mens det omvendte operasjonen av makt kan være beregnet på en effektiv måte.
La oss gå gjennom en enkel versjon av ElGamal som fungerer med tall modulo p. I tilfelle av elliptic curve varianter, det er basert på ganske ulike antall systemer.,
Generasjon av ElGamal nøkkelpar
Hver bruker av ElGamal nøkkel genererer nøkkelpar til som følger −
– >
-
Velge et stort primtall p. Generelt et primtall på 1024 2048 bits lengde er valgt.
-
Velge en generator element g.
-
Dette tallet må være mellom 1 og s − 1, men kan ikke være et tall.
-
Det er en generator av multiplicative gruppe av heltall modulo p. Dette betyr at for hvert heltall m co-prime til side, det er et heltall k slik at gk=en mod n.,
For eksempel, 3 generator for gruppe 5 (Z5 = {1, 2, 3, 4}).
-
| N | 3n | 3n mod 5 |
|---|---|---|
| 1 | 3 | 3 |
| 2 | 9 | 4 |
| 3 | 27 | 2 |
| 4 | 81 | 1 |
-
Velge den private nøkkelen. Den private nøkkelen x er et tall større enn 1 og mindre enn s−1.
-
Computing del av den offentlige nøkkelen., Verdien y er regnet ut fra de parametrene p, g og den private nøkkelen x som følger −
– >
y = gx mod p
-
Innhenting av Offentlige nøkkel. Den ElGamal offentlig nøkkel består av tre parametre (p, g, y).
For eksempel, la oss anta at p = 17 og at g = 6 (Det kan bekreftes at 6 er en generator av gruppen Z17). Den private nøkkelen x kan være et tall større enn 1 og mindre enn 71, så vi velger x = 5. Verdien y er deretter beregnet som følger −
– >
y = 65 mod 17 = 7
-
Dermed den private nøkkelen er 62 og den offentlige nøkkelen er (17, 6, 7).,
Kryptering og Dekryptering
generering av en ElGamal nøkkelpar er relativt enklere enn tilsvarende prosess for RSA. Men kryptering og dekryptering er litt mer komplisert enn RSA.
ElGamal-Kryptering
la oss Anta at avsender ønsker å sende en ren tekst til noen som ElGamal offentlig nøkkel er (p, g, y), deretter −
– >
-
Avsender representerer ren tekst som en serie av tall modulo p.
-
for Å kryptere den første klartekst S, som er representert som et tall modulo p., Krypteringsprosessen å få ciphertext C er som følger: −
– >
- Automatisk generere et tall k;
- Beregn to verdier C1 og C2, hvor −
C1 = gk mod pC2 = (P*yk) mod p
-
Send ciphertext C, som består av to separate verdier (C1, C2), sendt sammen.,
-
Henviser til vår ElGamal nøkkelgenerering eksempel gitt ovenfor, ren tekst P = 13 er kryptert som følger −
– >
- Tilfeldig generere en del, si k = 10
- Beregn to verdier C1 og C2, der −
C1 = 610 mod 17C2 = (13*710) mod 17 = 9
-
Send ciphertext C = (C1, C2) = (15, 9).,
ElGamal Dekryptering
-
for Å dekryptere ciphertext (C1, C2) ved bruk av privat nøkkel x, følgende to skritt er tatt −
– >
-
Beregne modulær invers av (C1)x modulo p, som er (C1)-x , vanligvis referert til som dekryptering faktor.,
-
Få tak i ren tekst ved hjelp av følgende formel −
– >
-
C2 × (C1)-x mod p = Plaintext
-
I vårt eksempel, å dekryptere ciphertext C = (C1, C2) = (15, 9) ved bruk av privat nøkkel x = 5, dekryptering faktor er
15-5 mod 17 = 9
-
Hent ren tekst P = (9 × 9) mod 17 = 13.
ElGamal Analyse
I ElGamal system, hver bruker har en privat nøkkel x. og har tre komponenter av offentlig nøkkel − prime modulus p, generator g, og offentlig Y = gx-mod p., Styrken av ElGamal er basert på vanskeligheten av diskrete logaritmen problem.
Den sikre viktige størrelse er vanligvis > 1024 bits. I dag selv 2048 bits lenge tasten er brukt. På behandlingen hastighet foran, Elgamal er ganske treg, den brukes hovedsakelig for nøkkel-godkjenning protokoller. På grunn av høyere behandling effektivitet, Elliptic Curve varianter av ElGamal blir stadig mer populært.,
Elliptic Curve Kryptografi (ECC)
Elliptic Curve Kryptografi (ECC) er et begrep som brukes for å beskrive en suite av kryptografiske verktøy og protokoller som sikkerhet er basert på spesielle versjoner av diskrete logaritmen problem. Det spiller ikke bruke tall modulo p.
ECC er basert på sett med tall som er forbundet med matematiske objekter som kalles elliptiske kurver. Det er regler for hvordan du legger til og computing multipler av disse tallene, akkurat som det er for tall modulo p.,
ECC har et varianter av mange kryptografiske ordninger som i utgangspunktet var designet for modulær tall som ElGamal kryptering og Digital Signatur Algoritme.
Det er antatt at den diskrete logaritmen problemet er mye vanskeligere når den brukes til poeng på en elliptic curve. Dette får bytte fra tall modulo p til poeng på en elliptic curve. Også et tilsvarende sikkerhetsnivå kan oppnås med kortere tastene hvis vi bruker elliptic curve-baserte varianter.,
Den kortere tastene resultere i to fordeler −
– >
- Letthet av key management
- Effektiv beregninger
Disse fordelene gjør elliptic-kurve-baserte varianter av kryptering ordningen svært attraktive for program der computing ressurser er begrenset.
RSA og ElGamal Ordninger – En Sammenligning
La oss raskt sammenlikne de RSA og ElGamal ordninger på ulike aspekter.
| RSA | ElGamal |
|---|---|
| Det er mer effektivt for kryptering. | Det er mer effektivt for dekryptering., |
| Det er mindre effektive for dekryptering. | Det er mer effektivt for dekryptering. |
| For et bestemt sikkerhetsnivå, lange tastene er nødvendig i RSA. | For samme nivå av sikkerhet, svært kort tastene er nødvendig. |
| Det er allment akseptert og brukt. | Det er nytt og ikke veldig populær i markedet. |