Correlational Forskning: Søker Relasjoner Mellom Variabler
I motsetning til beskrivende forskning, som er utviklet primært for å gi statiske bilder, correlational forskning innebærer måling av to eller flere relevante variabler og en vurdering av forholdet mellom eller blant de variablene., For eksempel variabler av høyde og vekt er systematisk relatert (korrelert) fordi folk generelt høyere veie mer enn kortere folk. På samme måte, studere tid og minne feil er også i slekt, fordi jo mer tid en person er gitt for å studere en liste av ord, færre feil han eller hun vil gjøre. Når det er to variabler i forskning, design, en av dem er kalt prediktor variabel og det andre utfallet variabel., Forskningen design kan visualiseres som dette, der buet pil representerer forventet korrelasjon mellom to variabler:
Figur 2.2.2

En måte å organisere data fra en correlational studie med to variabler er å plotte verdiene for hver av de målte variablene ved hjelp av et spredningsplott. Som du kan se i Figur 2.10 «Eksempler på Scatter Plott», et scatter-plot er et visuelt bilde av forholdet mellom to variabler., Et punkt er plottet for hvert individ i skjæringspunktet mellom hans eller hennes poengsummer for de to variablene. Når sammenhengen mellom variablene på scatter plott kan være lett rundet av med en rett linje, som i del (a) og (b) av Figur 2.10 «Eksempler på Scatter Plott», variablene er sagt å ha en lineær sammenheng.
Når den rette linjen indikerer at personer som har over gjennomsnittlige verdier for en variabel også en tendens til å ha over gjennomsnittlige verdier for andre variable, som i del (a), forholdet sies å være positiv lineær., Eksempler på positive lineære relasjoner omfatter de mellom høyde og vekt, mellom utdanning og inntekt, og mellom alder og matematiske evner hos barn. I hvert fall folk som scorer høyere på en av variablene har også en tendens til å score høyere på den andre variabelen. Negative lineære relasjoner, i kontrast, som vist i del (b), oppstår når over gjennomsnittlige verdier for en variabel har en tendens til å være assosiert med under gjennomsnittet verdier på den andre variabelen., Eksempler på negative lineære relasjoner omfatter de mellom alder av barn og antall bleier barnet bruker, og mellom praksis på, og feil som er gjort på en lærerik oppgave. I disse tilfeller mennesker som scorer høyere på en av variablene har en tendens til å skåre lavere på den andre variabelen.
Relasjoner mellom variabler som ikke kan beskrives med en rett linje er kjent som ikke-lineære relasjoner. Del (c) Figur 2.10 «Eksempler på Scatter Plott» viser et felles mønster der fordelingen av poeng er egentlig tilfeldig., I dette tilfellet er det ikke forhold på alle mellom de to variablene, og de er sagt å være uavhengige. Deler (d) og (e) av Figur 2.10 «Eksempler på Scatter Plott» vis mønstre av sammenslutning der, selv om det er en sammenheng, poeng er ikke godt beskrevet av en enkelt rett linje. For eksempel, en del (d) viser den type forhold som ofte oppstår mellom angst og ytelse., Økning i angst fra lave til moderate nivåer er assosiert med ytelsen øker, mens økning i angst fra moderate til høye nivåer er forbundet med en nedgang i ytelse. Forhold som endrer seg i retning og dermed er ikke beskrevet ved en enkelt rett linje kalles kurvelineære relasjoner.
Figur 2.10 Eksempler på Scatter Plott
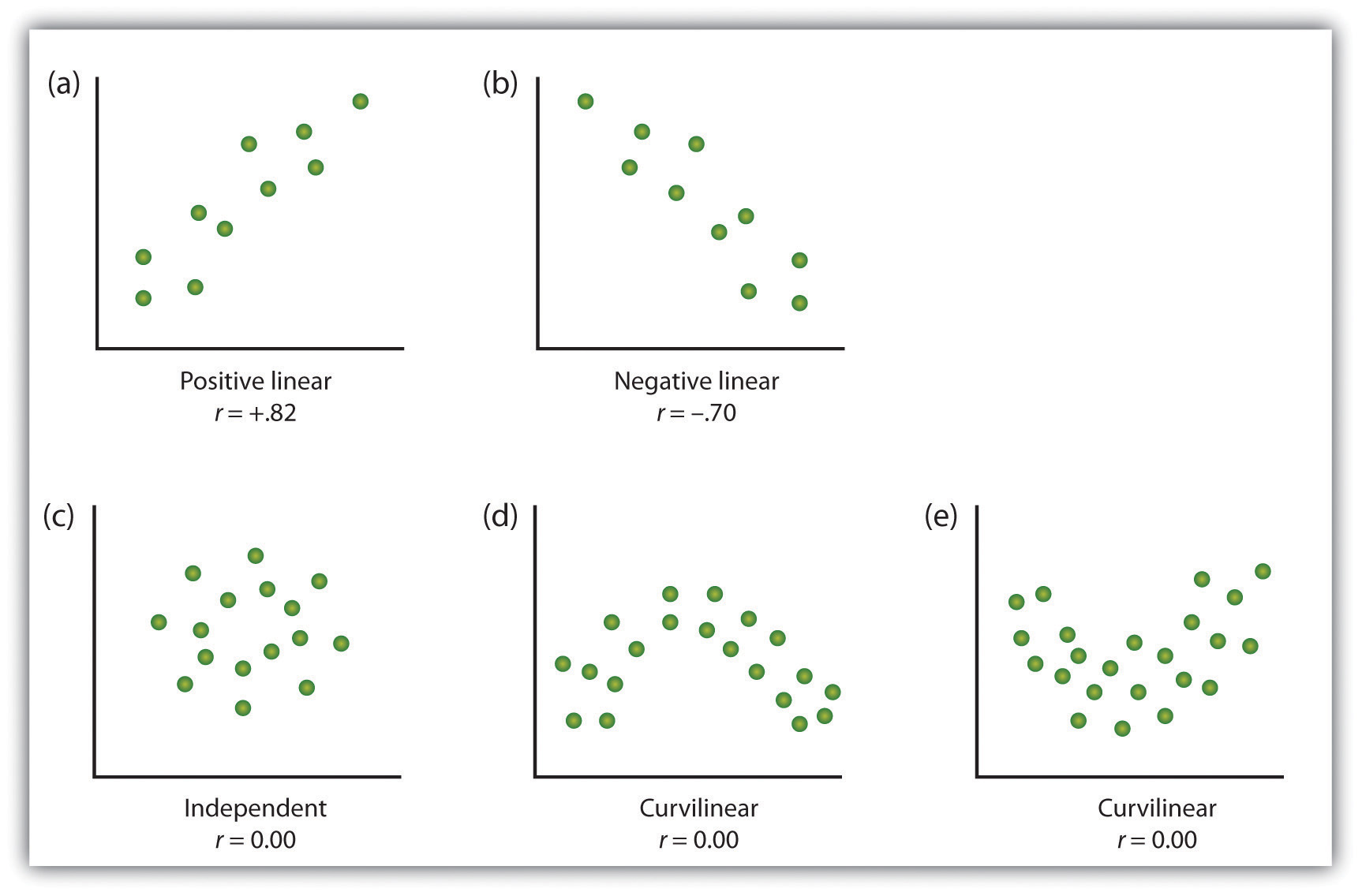
Noen eksempler på sammenhenger mellom to variabler som vist i scatter plott., Vær oppmerksom på at Pearson korrelasjonskoeffisient (r) mellom variablene som har kurvelineære relasjoner vil trolig være nær null.
Tilpasset fra Stangor, C. (2011). Forskning metoder for behavioral sciences (4. utg.). Mountain View, CA: Cengage.
De mest vanlige statistiske mål på styrken av lineære relasjoner mellom variabler er Pearson korrelasjonskoeffisient, som er symbolisert ved bokstaven r. Verdien av korrelasjonskoeffisienten varierer fra r = -1.00 til r = +1.00., Retningen på den lineære forholdet er merket med tegn på korrelasjonskoeffisienten. Positive verdier av r (for eksempel r = .54 eller r = .67) tyder på at sammenhengen er positiv lineær (dvs., mønster av punkter på punktplott går fra nedre venstre til øvre høyre), mens negative verdier av r (for eksempel r = –.30 eller r = –.72) indikerer negative lineære relasjoner (dvs., prikkene går fra øvre venstre til nedre høyre hjørne). Styrken av det lineære forholdet er indeksert av avstanden til korrelasjonskoeffisienten fra null (absolutt verdi)., For eksempel, r = –.54 er et sterkere forhold enn r = .30, – og r = .72 er et sterkere forhold enn r = –.57. Fordi Pearson korrelasjonskoeffisient bare måler lineær relasjoner, variabler som har kurvelineære sammenhenger er ikke godt beskrevet av r, og den observerte korrelasjonen vil være nær null.
Det er også mulig å studere relasjoner mellom mer enn to mål på samme tid., Et forsknings-design der mer enn en prediktor variabelen brukes til å forutsi et enkelt utfall variabel er analysert gjennom flere regresjon (Aiken & Vest, 1991). Multippel regresjonsanalyse er en statistisk teknikk, basert på korrelasjon koeffisienter mellom variabler, som gjør det mulig å forutsi et enkelt utfall variabel fra mer enn en prediktor variabel. For eksempel, Figur 2.11 «Prediksjon av Jobben Ytelse Fra Tre Prediktor Variabler» viser en multippel regresjonsanalyse der tre prediktor variabler brukes til å forutsi et enkelt utfall., Bruk av multippel regresjonsanalyse viser en viktig fordel av correlational forskning design—de kan brukes til å gjøre forutsigelser om en person er sannsynlig score på et utfall variabel (f.eks., jobbutførelse) basert på kunnskap om andre variabler.
Figur 2.11 anslag på Jobb Ytelse Fra Tre Prediktor Variabler
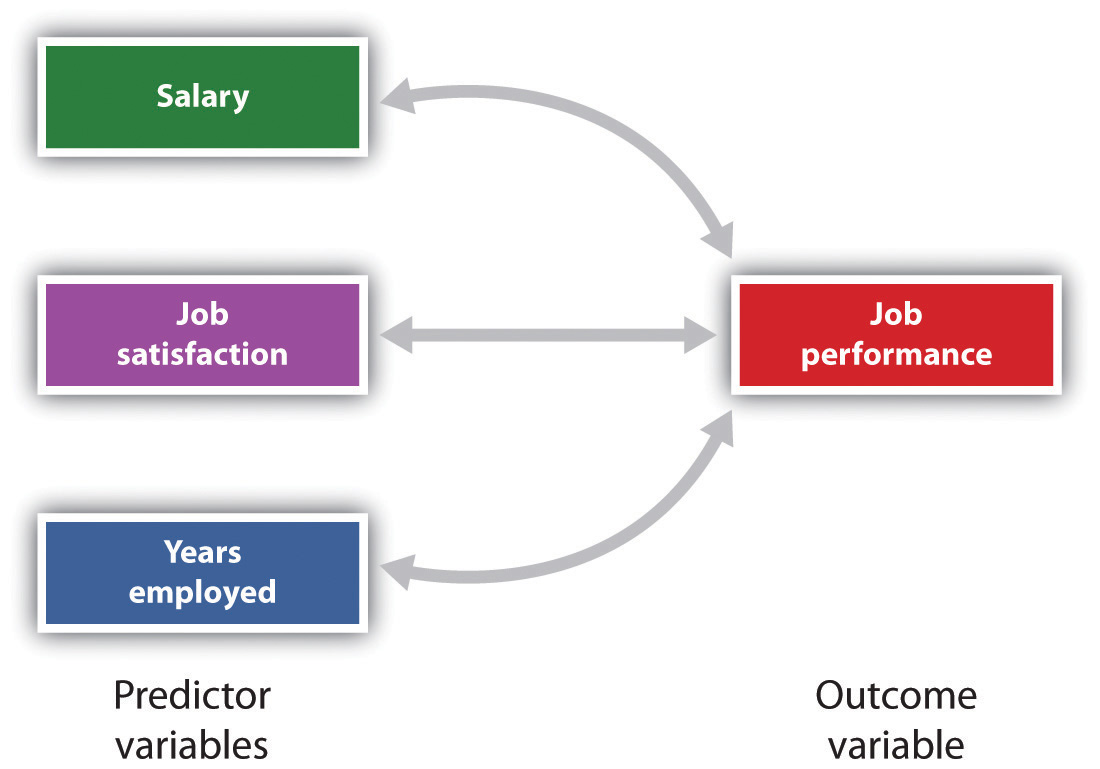
Flere regresjon tillater forskere å forutsi score på et enkelt utfall variabel ved hjelp av mer enn en prediktor variabel.,
En viktig begrensning av correlational forskning design er at de ikke kan brukes til å trekke konklusjoner om kausale relasjoner mellom de målte variablene. Tenk, for eksempel, en forsker som har en hypotese om at du viser voldelig atferd vil føre til økt aggressiv spiller i barn. Han har samlet inn fra et utvalg av fjerde klasse barn, et mål på hvor mange voldelige tv-serier hvert barn visninger i løpet av uken, så vel som et mål på hvor aggressivt hvert barn spiller på skolens lekeplass., Fra hans innsamlede data, forsker oppdager en positiv korrelasjon mellom de to målte variabler.
Selv om denne positive sammenhengen ser ut til å støtte researcher ‘ s hypotese, det kan ikke bli tatt for å indikere at du viser voldelige tv-fører til aggressiv atferd. Selv om forskeren er fristet til å anta at visning av voldelige tv-fører til aggressiv spiller,
Figur 2.2.2

det finnes også andre muligheter., En alternativ mulighet er at den kausale retningen er nøyaktig motsatt fra hva som har vært hypotese. Kanskje barn som har oppført seg aggressivt på skolen utvikle gjenværende spenning som fører dem til å ha lyst til å se voldelige tv-serier hjemme:
Figur 2.2.2

Selv om denne muligheten kan virke mindre sannsynlig, det er ingen måte å utelukke muligheten for slike omvendt kausalitet på grunnlag av denne observert sammenheng., Det er også mulig at både kausale retningene er i drift og at de to variablene føre til hverandre:
Figur 2.2.2

Likevel en annen mulig forklaring på den observerte sammenhengen er at det har blitt produsert av tilstedeværelsen av en felles-kausal variabel (også kjent som en tredje variabel)., En felles-kausale variabel er en variabel som ikke er en del av den forskning hypotesen, men som fører til både prediktor og utfallet variabel, og dermed gir den observerte korrelasjonen mellom dem. I vårt eksempel en potensiell felles-kausale variabel er disiplin stil av barnas foreldre. Foreldre som bruker en streng og straffende disiplin stil kan produsere barn som både liker å se voldelige tv-og som oppfører seg aggressivt i forhold til barn med foreldre som bruker mindre harde disiplin:
Figur 2.2.,2
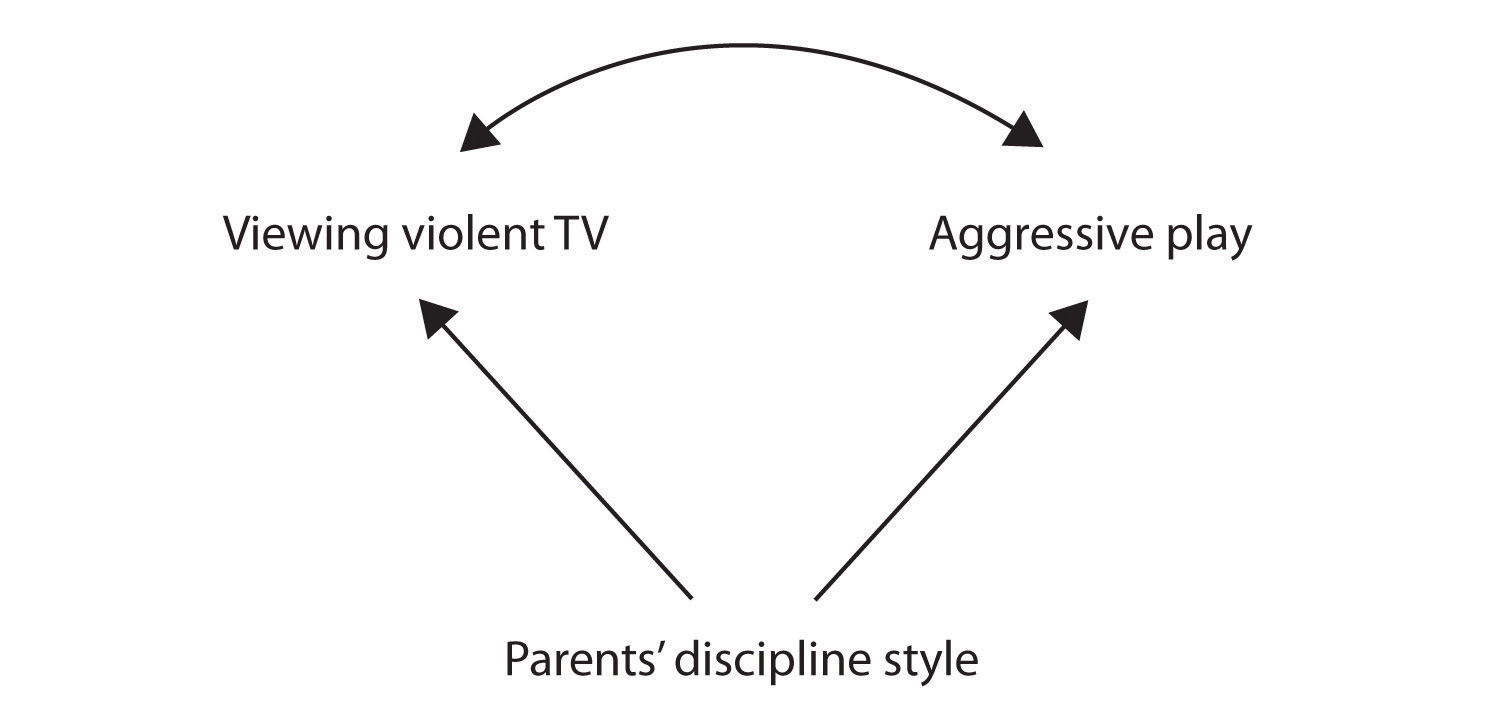
I dette tilfellet, tv-titting og aggressivt spill ville være positivt korrelert (som indikert av buet pil mellom dem), selv om ingen av dem er forårsaket av andre, men de var begge forårsaket av disiplin stil av foreldre (den rette piler). Når prediktor og variablene er begge forårsaket av en felles-kausale variabel, det observerte forholdet mellom dem er sagt å være forfalskninger., En falsk forhold er et forhold mellom to variabler der en felles-kausale variabel produserer og forklarer unna» relasjon. Hvis virkninger av felles-kausal variabelen ble tatt bort, eller er kontrollert for, forholdet mellom prediktor og variablene ville forsvinne. I eksempel forholdet mellom aggresjon og tv-titting kan være falske, fordi ved å kontrollere for effekten av foreldrenes disiplinere stil, forholdet mellom tv-titting og aggressiv atferd kan gå bort.,
Felles-kausale variabler i correlational forskning design kan ses som et «mysterium» variabler fordi, som de ikke har blitt målt, er deres tilstedeværelse og identitet er som regel ukjent for forskeren. Siden det ikke er mulig å måle hver variabel som kan føre til både prediktor og variablene, eksistensen av en ukjent felles-kausale variabel er alltid en mulighet. På grunn av dette, sitter vi igjen med grunnleggende begrensning av correlational forskning: Korrelasjon ikke påvise årsakssammenheng., Det er viktig at når du leser om correlational forskningsprosjekter, må du huske på muligheten for falske relasjoner, og sørg for å tolke resultatene riktig. Selv om correlational forskning er noen ganger rapportert som viser kausalitet uten noen nevne blir laget av muligheten for omvendt kausalitet eller felles-kausale variabler, informerte forbrukere av forskning, som du, du er klar over disse interpretational problemer.
I sum, correlational forskning design har både styrker og begrensninger., En styrke er at de kan brukes når eksperimentell forskning er ikke mulig fordi prediktor variabler kan ikke være manipulert. Correlational design også har fordelen ved at forskeren å studere atferd som oppstår i hverdagen. Og vi kan også bruke correlational design for å gjøre spådommer, for eksempel til å forutsi fra score på sine batteri av tester lykkes i jobben lærlinger under en treningsøkt. Men vi kan ikke bruke slike correlational informasjon til å avgjøre om opplæring forårsaket bedre jobb ytelse. For at forskere stole på eksperimenter.,