konfidensintervall og p-verdier
for å kunne ha noen som helst diskusjon av statistisk analyse, er det viktig å først forstå konseptet av befolkningen statistikk. Tydelig, er befolkningen statistikk er verdiene av alle tiltak innenfor populasjonen, og estimere dem er målet for de fleste studier ., For eksempel, i en studie ser på fedme priser for pasienter på en viss medisinering, befolkningen statistikk kan være gjennomsnittlig fedme pris for alle pasienter på medisiner.
Imidlertid identifisere denne verdi ville kreve å ha data for hvert enkelt individ som faller inn i denne kategorien, noe som er upraktisk. I stedet, en randomisert eksempel kan være samlet, som eksempel statistikk kan bli innhentet. Disse utvalget statistikk tjene som estimater av tilsvarende befolkningen statistikk og tillate en forsker for å gjøre slutninger om en populasjon av interesse.,
En betydelig begrensning finnes i at disse bygget prøvene skal være representative for større populasjon av interesse. Mens det er mange tiltak som kan iverksettes for å redusere denne begrensning, noen ganger dens virkninger (såkalte prøvetaking bias ) gå utover kontroll av forskeren. I tillegg, selv i en teoretisk situasjon med ingen prøvetaking bias, randomisering kan resultere i en misrepresentative eksempel. I forrige eksempel, la oss anta at befolkningen frekvensen av fedme blant alle voksne kvalifisert for medisiner var 25%., I et enkelt tilfeldig utvalg av 30 pasienter fra denne populasjonen, det er en 19.7% sjanse for at minst 10 pasienter vil være overvektige, noe som resulterer i en prøve fedme pris av 33.3% eller enda høyere. Selv om det er ingen sammenheng mellom medisinering og fedme priser, det er fortsatt mulig å møte en pris som ser ut til å være forskjellige fra den generelle fedme pris, noe som skjedde gjennom tilfeldigheten i prøvetaking alene. Denne effekten er det grunn for rapportering av konfidensintervall og p-verdier i klinisk forskning.
konfidensintervaller er intervaller hvor befolkningen statistikk kan lyve., De er konstruert basert på eksempel statistikk og enkelte funksjoner, for eksempel måle hvor sannsynlig det er å være representant og rapporteres til en viss terskel . Et 95% konfidensintervall er et intervall konstruert slik at det i gjennomsnitt 95% av stikkprøver vil inneholde den sanne befolkningen statistikk innenfor sine 95% konfidensintervall. Dermed er en terskel for signifikante resultater er ofte tatt som 95%, med den forståelse at alle verdier innenfor det meldte området er like gyldig som mulig befolkningen statistikk.,
p-verdi rapporter lignende informasjon på en annen måte. Snarere enn å bygge et intervall rundt et eksempel statistikk, og p-verdien viser sannsynligheten for at prøven statistikken ble produsert fra tilfeldig utvalg av en populasjon, gitt et sett av forutsetninger om befolkningen, referert til som «null-hypotesen» ., Ta for eksempel studere på fedme priser igjen, fedme pris blant eksempel (et eksempel av pasienter på medisiner) kan bli rapportert sammen med en p-verdi bestemme sjanse for at en slik pris kan være produsert fra tilfeldig sampling den samlede populasjon av pasienter kvalifisert for medisinering. I tilfelle av studiet, null-hypotesen er at befolkningen frekvensen av fedme blant pasienter på medisiner er lik den totale frekvensen av fedme blant alle pasienter kvalifisert for medisinering, som er 25%., En one-tailed p-verdi kan brukes hvis det er grunn til å tro at en effekt som ville skje i bare én retning (for eksempel, kan det være grunn til å tro at medisinen ville øke vektøkning, men ikke redusere det), mens en to-tailed p-verdien som skal brukes i alle andre tilfeller. Når du bruker en symmetrisk distribusjon, slik som normal distribusjon, to-tailed p-verdier er ganske enkelt to ganger på ett-tailed p-verdi.
Tenk deg igjen at en prøve av 30 pasienter på medisiner inneholder 12 overvektige individer. Med en one-tailed test, våre p-verdien er 0.0216 (ved hjelp av binomiske fordelingen)., Dermed kan vi si at vår observert pris av 40% er vesentlig forskjellig fra en hypotese om pris på 25% ved en betydning nivå på 0,05. I en annen forstand, 95% konfidensintervall for den observerte andelen er 25.6% til 61.07%. Konfidensintervaller svarer til to-tailed tester, hvor en to-tailed testen er avvist hvis og bare hvis konfidensintervallet inneholder ikke verdien assosiert med nullhypotesen (i dette tilfellet, 25%).
Hvis en beregnet p-verdien er liten, er det sannsynlig at bestanden er ikke strukturert som opprinnelig angitt i nullhypotesen., Hvis vi får en lav p-verdi, vi har bevis på at det ikke var noen effekt eller årsaken til den observerte forskjellen – medisiner, i dette tilfellet. En grenseverdi på 0,05 (eller 5%) brukes vanligvis, med en p-verdi har til å være under denne grensen for det tilsvarende attributtet til å være statistisk signifikant.
Risk ratio
Risikoen, et annet uttrykk for sannsynlighet, er et annet grunnleggende prinsipp for statistisk analyse. Sannsynlighet er en sammenligning av observert en bestemt hendelse som oppstår som et resultat av totalt antall unike resultater., En mynt flip er et trivielt eksempel: risikoen for å observere en heads ½ % eller 50%, som på alle mulige unike studier (en flip resulterer i hodet eller en flip resulterer i mynt), bare man er arrangementet av interesse (hoder).
ved Hjelp av bare risiko kan spådommer om en enkelt bestand. For eksempel, se på fedme priser innen den AMERIKANSKE befolkningen, CDC rapportert at 42.4% av voksne var overvektige i 2017-2018. Så, risikoen for en person i USA blir overvektige er rundt 42.4% . Men de fleste studier som ser på effekten av en spesifikk intervensjon eller andre element (f.eks. dødelighet) på en annen., Tidligere, har vi antatt at fedme pris av kvalifisert pasienter var 25%, men her vil vi bruke 42.4% assosiert med USA voksne befolkningen. Anta at vi observere en risiko for 25% i et tilfeldig utvalg av pasienter på medisiner så vel. For å forklare effekten av medisinen på fedme, et logisk neste skritt ville være å dele risiko for fedme i den AMERIKANSKE befolkningen på medisiner med risiko for fedme i den AMERIKANSKE befolkningen, noe som resulterer i en risiko-forholdet til 0.590.,
Denne beregningen – et forhold mellom to sjanser – er hva som menes med den selvtitulerte risk ratio (RR) statistikk, også kjent som relativ risiko. Det gjør at et bestemt nummer vil bli gitt for hvor mye risiko en person i én kategori bjørner i forhold til en person i en annen kategori. I eksempel en person å ta medisinen bærer 0.59 ganger så mye risiko som en voksen fra den generelle AMERIKANSKE befolkningen., Vi har imidlertid antatt at befolkningen kvalifisert for medisinering hadde en overvekt pris av 25% – kanskje bare en gruppe unge voksne, som kan være sunnere i gjennomsnitt, er kvalifisert til å ta medisiner. Når vi undersøker effekten av medisinen på fedme, dette er den andelen som skal brukes som null-hypotesen. Hvis vi observerer en fedme pris på medisinering av 40%, med en p-verdi mindre enn betydningen nivå på 0,05, dette er bevis på at medikamenter øker risikoen for fedme (med en RR, i dette tilfellet, 1.6)., Som sådan, er det viktig å nøye velge nullhypotesen for å gjøre relevante statistiske prediksjoner.
Med RR, et resultat av 1 betyr at begge grupper har samme grad av risiko, mens resultatene ikke er lik 1 betyr at én gruppe bar mer risiko enn en annen, en risiko som er antatt å skyldes intervensjonen undersøkt av studiet (formelt, forutsetningen om kausal retning).
for Å illustrere, kan vi se på resultatene av en 2009 studie publisert i Journal of Hjerneslag og Cerebrovaskulær sykdom., Studien rapporterer at pasienter med et langvarig electrocardiographic QTc-intervallet var mer sannsynlig å dø innen 90 dager sammenlignet med pasienter uten en lengre intervall (relativ risiko =2.5; 95% konfidensintervall 1.5-4.1) . Å ha et konfidensintervall mellom 1,5 og 4.1 for risiko-forholdet indikerer at pasienter med en forlenget QTc-intervall var på 1,5-4.1 ganger mer sannsynlig å dø i løpet av 90 dager enn de uten en forlenget QTc-intervall.,
Et annet eksempel – i en landemerke-papir som viser at blodtrykket kurve i akutt hjerneinfarkt er U-formet snarere enn J-formet , etterforskerne fant at RR økt nesten to ganger i pasienter med gjennomsnittlig arterielt blodtrykk (MAP) >140 mmHg eller <100 mmHg (RR=1.8, 95% KI 1.1-2.9, p=0.027). Å ha en CI 1,1-2,9 for den RR betyr at pasienter med et KART utenfor rekkevidden av 100-140 mmHg var 1,1-2.9 ganger mer sannsynlig å dø, enn de som hadde første KART i denne serien.,
For et annet eksempel, en 2018 studie av Australske marinen rekrutter fant at de med prefabrikkerte ortoser (en type foten støtte) hadde en 20.3% risiko for lidelse minst en ugunstig effekt, mens de som ikke hadde en risiko på 12,4% . En risiko-forhold her er gitt ved 0.203/0.124, eller 1.63, noe som tyder på at rekrutter med fot ortoser bar 1,63 ganger risikoen for å ha noen negativ konsekvens (e.g. foten blemme, smerte, osv.) enn de uten. Imidlertid, den samme undersøkelsen rapporterer et 95% konfidensintervall for risiko ratio av 0.96 å 2.76, med en p-verdi på 0.068., Se på konfidensintervallet, 95% rapporterte utvalg (den allment aksepterte standard) omfatter verdier under 1, 1, og verdier over 1. Husk at alle verdier er like stor sannsynlighet for å bli befolkningen statistikk, i 95% konfidens, det er ingen måte å utelukke muligheten for at fot ortoser har ingen effekt, har en vesentlig fordel, eller har en betydelig ulempe. I tillegg, p-verdien er større enn det som er standard på 0,05, derfor er denne data ikke gir betydelige bevis på fot ortoser å ha noen konsistent effekt på uønskede hendelser som for eksempel blemmer og smerter., Som nevnt tidligere, dette er ingen tilfeldighet – hvis de er beregnet ved hjelp av de samme eller lignende metoder, og p-verdien er to-tailed, konfidensintervall og p-verdier vil rapportere de samme resultatene.
Når det benyttes riktig, risiko ratio er et kraftig statistikk som gir et anslag i en populasjon av endring i risiko en befolkning bærer over en annen., De er ganske lett å forstå (verdien er hvor mange ganger den risiko en gruppe bærer over en annen), og med den forutsetning av kausal retning, raskt vise om en intervensjon (eller andre testet variabelen) har en effekt på utfallet.
Men det finnes begrensninger. For det første, RRs, kan ikke brukes i alle tilfeller. Fordi risikoen i et eksempel er et anslag av risiko i en befolkning, må prøven være rimelig representative for befolkningen. Som sådan, case-kontroll studier, ved en enkel grunn av det faktum at prosenter av resultatene er kontrollert, kan ikke ha en risiko-forholdet er rapportert., For det andre, som med all statistikk er beskrevet i denne avtalen, RR er et relativt mål, og gir informasjon om risiko i en gruppe i forhold til en annen. Problemet her er at en studie hvor to grupper hadde en risiko på 0,2% og 0,1% bærer samme RR, 2, så en hvor to grupper hadde en risiko for 90% og 45%. Men i begge tilfeller er det sant at de med intervensjonen var på det dobbelte av den risiko dette utgjør kun 0,1% mer risiko i ett tilfelle, mens 45% mer risiko i en annen sak., Dermed, rapportering bare RR overdriver effekten i første omgang, mens potensielt selv minimere effekten (eller i det minste decontextualizing det) i det andre tilfellet.
Odds ratio
Mens risikoen rapporter antall hendelser som er av interesse i forhold til det totale antall forsøk, odds rapportere antall hendelser som er av interesse i forhold til antall hendelser ikke er av interesse. Forklart på en annen måte, det rapporter antall hendelser for å nonevents., Mens risikoen, som definert tidligere, for å snu en mynt til å være leder er 1:2 eller 50%, oddsen for å snu en mynt til å være leder er 1:1, så det er en ønsket utfall (event), og en uønsket utfall (nonevent) (Figur 1).
– >
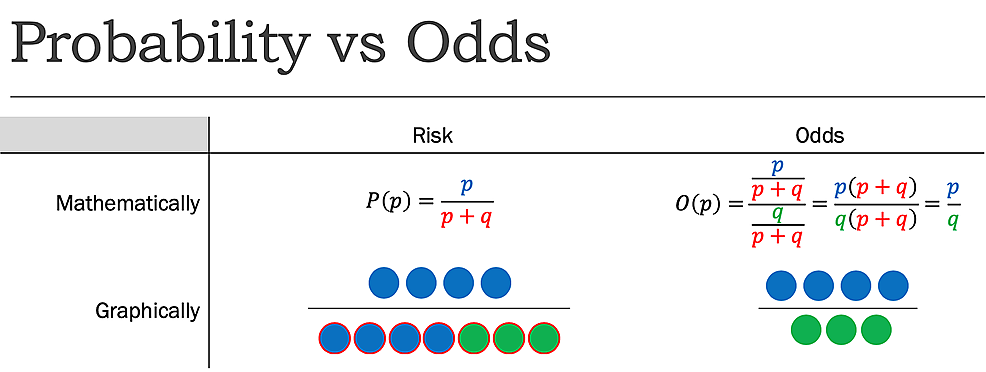
Figure1:Sannsynlighet (P) vs. Odds (O) der p=sannsynlighet for suksess og q=sannsynligheten for svikt
Akkurat som med RR, hvor forholdet mellom to risikoene ble tatt for to separate grupper, forholdet mellom to odds kan bli tatt for to separate grupper for å produsere en odds ratio (ELLER)., I stedet for å rapportere hvor mange ganger den risiko en gruppe bjørner i forhold til de andre, rapporter hvor mange ganger odds en gruppe bærer til den andre.
For de fleste, er dette en vanskeligere statistikk for å forstå. Risiko er ofte en mer intuitiv konsept enn oddsen, og dermed forstå relativ risiko er ofte foretrukket å forstå i forhold odds. Imidlertid, ELLER ikke lider av de samme årsakssammenheng forutsetning begrensninger som RR, noe som gjør det mer allment gjeldende.,
For eksempel, oddsen er et symmetrisk mål, noe som betyr at mens risiko bare undersøker resultatene gitt tiltak, odds kan også undersøke intervensjoner gitt resultater. Dermed, en studie kan bygges der, heller enn å rettssaken grupper og måling av utfall, utfall kan bli valgt, og andre faktorer som kan analyseres. Følgende er et eksempel på en case-kontroll studie, en situasjon hvor RR ikke kan brukes, men er ELLER kan.
En 2019 case-kontroll studie viser seg å være et godt eksempel., Søker å finne potensielle sammenheng mellom hepatitt A virus (HAV) infeksjon fremtredende i Canada og noen forårsaker faktor, en studie ble konstruert basert på utfallet (med andre ord, personer ble kategorisert basert på deres HAV status som «intervensjon», eller utløsende hendelsen, var ukjent). Studien så på de med HAV og de uten, og hva slags mat de hadde spist før HAV-infeksjon . Fra denne, flere odds ratio ble konstruert for å sammenligne en bestemt mat element til HAV status., For eksempel, data fant at blant de fagene som hadde eksponering for scampi/reker, åtte var positive for HAV mens sju ble det ikke, mens for de uten eksponering to var positive for HAV og 29 ble det ikke. En odds ratio er tatt av (8:7)/(2:29) som tilsvarer ca 16.6. Studien data rapportert en ELLER av 15,75, med små avvik sannsynlig stammer fra en pre-beregning justering for konfunderende variabler som ikke var omtalt i avisen. En p-verdi på 0,01 ble rapportert, og dermed gi statistiske bevis for dette, ELLER å være betydelig.,
Dette kan tolkes på to likeverdige måter. For det første, oddsen for reker/reke eksponering for de med HAV er 15.75 ganger høyere enn for dem uten. Tilsvarende oddsen for HAV-posiitve versus HAV-negative er 15.75 ganger høyere for de som utsettes for reker/reker enn for de som ikke er eksponert.
Samlet, ELLER gir et mål på styrken på sammenhengen mellom to variabler på en skala fra 1 er ingen forening, over 1 å være en positiv sammenheng, og under 1 være en negativ assosiasjon., Mens de foregående to tolkninger er riktige, de er ikke så direkte forståelig som en RR ville ha blitt, hadde det vært mulig å finne én. En alternativ tolkning er at det er en sterk positiv korrelasjon mellom scampi/reker eksponering og HAV.
på Grunn av dette, i enkelte tilfeller er det hensiktsmessig å omtrentlig RR med ELLER. I slike tilfeller, den sjeldne sykdommen forutsetningen må holde. Det er en sykdom som må være svært sjelden i en befolkning., Under denne saken, risikoen for sykdom i befolkningen (p/(p+q)) tilnærminger oddsen for sykdom i befolkningen (p/q) som s blir insignificantly liten i forhold til sp. Dermed RR og ELLER konvergere som befolkningen blir større. Imidlertid, hvis denne forutsetningen svikter, forskjellen blir stadig mer overdrevet. Matematisk sett, i p+q prøvelser, avtagende p øker q for å opprettholde samme sum prøvelser. Med fare, bare teller endringer, mens med odds både teller og nevner endre seg i motsatt retning., Som et resultat, for tilfeller hvor RR og ELLER begge er under 1, ELLER vil undervurdere RR, mens for de tilfeller hvor begge er over 1, ELLER vil overvurdere RR.
Misreporting av ELLER som RR, så kan ofte overdrive data. Det er viktig å huske det, ELLER er et relativt mål, akkurat som RR, og dermed noen ganger kan en stor ELLER kan korrespondere med en liten forskjell mellom odds.
For de mest trofaste rapportering, da, ELLER bør ikke presenteres som en RR, og bør kun presenteres som en tilnærming av RR hvis den sjeldne sykdommen forutsetning rimelighet kan holde., Hvis det er mulig, en RR skal alltid rapporteres.
Hazard ratio
Både RR og ELLER bekymring tiltak og utfall, og dermed rapportering på tvers av hele studieperioden. Men en lignende, men tydelige mål, hazard ratio (HR), bekymringer priser of change (Tabell 1).
– >
| RR | ELLER | HR | |
| Mål | Bestemme forholdet i fare status basert på noen av variablene. | Fastslå sammenhengen mellom to variabler., | Avgjøre hvordan en gruppe endringer i forhold til en annen. |
| Bruker | Forteller oss hvordan en intervensjon endringer risiko. | Forteller oss om det er en sammenheng mellom et tiltak og risiko, anslår hvor denne foreningen gjelder. | Forteller oss hvordan en intervensjon endringer i pris for å oppleve en hendelse. |
| Begrensninger | gjelder Bare hvis studiedesign er representative for befolkningen. Kan ikke bruke på case-kontroll studier. | Kan generelt brukes overalt, men ikke alltid en nyttig statistikk i seg selv. Overdriver risikoen., | typisk være nyttig, og endring i to grupper bør være relativt konsistente. |
| Tidslinjen | Statisk – ikke vurdere priser. Oppsummerer et helhetlig studium. | Statisk – ikke vurdere priser. Oppsummerer et helhetlig studium. | Basert på priser. Gir informasjon om hvordan en studie utvikler seg over tid. |
Table1: Relativ risiko (RR) vs. Odds Ratio (ELLER) vs., Hazard Ratio (HR)
HRs er i tandem med survivorship kurver som viser den tidsmessige utviklingen av noen hendelse i en gruppe, om at arrangementet er død, eller trekke en sykdom. I en survivorship kurve, og den vertikale aksen tilsvarer tilfelle av interesse og den horisontale aksen tilsvarer tid. Faren for at arrangementet blir så tilsvarer stigningstallet til grafen, eller hendelser per time.
En hazard ratio er rett og slett en sammenligning av to farer., Det kan vise hvor raskt to survivorship kurver avviker gjennom en sammenligning av bakkene av kurver. En HR av 1 indikerer ingen avvik – både innen kurver, sannsynligheten for at hendelsen var like sannsynlig til enhver tid. HR-ikke lik 1 tilsier at to hendelser ikke skjer på en lik pris, og risikoen for at et individ i en gruppe som er annerledes enn risikoen for en person i en annen på et gitt tidsintervall.
En viktig forutsetning at HRs gjøre er proporsjonal priser forutsetning., For å rapportere en enestående hazard ratio, det må antas at de to hazard priser er konstant. Hvis skråningen av grafen er å endre forholdet vil på samme måte endres over tid, og dermed vil ikke gjelde som en sammenligning av sannsynligheten til enhver tid.
Vurdere prøveversjon av en roman kjemoterapeutiske agent som søker å forlenge levetiden for pasienter med en bestemt kreft. I både intervensjon-og kontroll gruppe, 25% hadde dødd av uke 40., Siden begge gruppene gikk ned fra 100% overlevelse til 75% overlevelse over 40-ukers periode, fare priser ville være like og dermed fare pris lik 1. Dette tyder på at en person som mottar stoffet er like sannsynlig å dø som en ikke får stoffet til enhver tid.
det er Imidlertid mulig at det i den intervention group, alle 25% døde mellom seks uker til 10, mens det i kontrollgruppen, alle 25% døde innen én til seks uker. I dette tilfellet, sammenligne medians ville vise en høyere forventet levealder for de som er på stoffet til tross for at HR ikke viser noen forskjell., I dette tilfellet er proporsjonal farer forutsetningen svikter, som det fare priser change (ganske dramatisk) over tid. I tilfeller som dette, HR er ikke aktuelt.
Fordi det er noen ganger vanskelig å avgjøre om proporsjonal farer forutsetning rimelig gjelder, og fordi du tar en HR strimler den opprinnelige måling (hazard priser) av tiden enhet, er det vanlig praksis å rapportere HR i forbindelse med median ganger.,
I en studie for å evaluere den prognostiske ytelse av Den Raske Akutt Medisin Score (REMS) og Worthing Fysiologiske Scoring system (WPSS), etterforskerne funnet at risikoen for 30-dagers dødelighet var økt med 30% for hver ekstra REMS enhet (HR: 1.28; 95% konfidensintervall (CI): 1.23-1.34) og med 60% for hver ekstra WPSS enhet (HR: 1.6; 95% CI: 1.5-1.7). I dette tilfellet, død pris ikke endret, men heller scoring system for å forutsi den gjorde det, så HR-kan brukes. Å ha et konfidensintervall mellom 1,5 og 1.,7 for WPSS farer forholdet indikerer at dødeligheten kurven for de med høyere WPS avtar på en raskere hastighet (ca 1,5-1,7 ganger). Siden den lave enden av intervallet er fortsatt over 1, vi er overbevist om at den sanne fare for død innen 30 dager er høyere for gruppen med høyere WPS .
I en 2018 studie på overstadig drikking blant personer med visse risikofaktorer, en overlevelse buen ble bygget plotting pris på å oppnå overstadig drikking for kontrollene, de med en familie historie, mannlig kjønn, de med høy impulsivitet, og de med høyere respons til alkohol., For menn og de med en familie historie, statistisk signifikante bevis for en høyere pris for å oppnå overstadig drikking ble rapportert (en HR av 1.74 for menn og 1.04 for de med en familie historie) . Men for de med høy impulsivitet, selv om HR var 1.17, 95% konfidensintervall varierte fra 1,00 til 1.37. Dermed, til et 95% konfidens nivå, det er umulig å utelukke at HR var 1.00.,
på Grunn av den overdrivelse til stede, er det viktig å unngå representerer Or som RRs, og på samme måte er det viktig å erkjenne at en rapportert ELLER sjelden gir en god tilnærming til relativ risiko, men heller bare gir et mål på samvariasjon.
på Grunn av sin evne til å gjøre fast konklusjoner og forståeligheten, RR skal rapporteres hvis det er mulig, men i de tilfeller hvor det er kausalitet forutsetningen er krenket (for eksempel kasus-kontroll studier og logistisk regresjon), ELLER det kan brukes.,
Timer er brukt med overlevelse kurver og anta at fare priser er lik over tid. Mens nyttig å sammenligne to priser, de skal rapporteres med median ganger for å rettferdiggjøre proporsjonal farer forutsetning.
til Slutt, uavhengig av verdien av HR/BH/ELLER statistikk, en tolkning bør bare gjøres etter at avgjørelsen av om resultatet gir statistisk signifikante bevis mot en konklusjon (som bestemmes av p-verdi eller konfidensintervall)., Å huske disse prinsippene og rammene for HR/BH/ELLER minimerer fremstilling og hindrer en fra å tegne feil konklusjoner fra resultatene av en publisert studie om ulike prøvene. Figur 2 oppsummerer riktig og feil bruk av disse ulike risiko forholdstall.
– >
