14.5: Pascal’ s Prinsipp og Hydraulikk

Programmer av Pascal ‘s Prinsipp og Hydrauliske Systemer

Vi kan utlede en sammenheng mellom kreftene i denne enkle hydrauliske systemet ved å bruke Pascal’ s prinsipp. Merk først at de to stempler i systemet er i samme høyde, så det er ingen forskjell i press på grunn av en forskjell i dybden. Presset på grunn av F1 handler på området A1 er rett og slett

\(p_{1} = \frac{F_{1}}{A_{1}}\), som er definert som \(p = \frac{F}{A}\).,

\

Denne ligningen gjelder forhold av makt i området i noen hydraulisk system, forutsatt at stemplene er på samme vertikal høyde og at friksjonen i systemet er ubetydelig.

Hydrauliske systemer kan øke eller redusere kraften som påføres dem. For å gjøre det større kraft, trykket er lagt til et større område. For eksempel, hvis en 100-N force er brukt til venstre sylinder i Figur 14.16 og rett sylinder har et område som er fem ganger større, så produksjonen force er 500 N., Hydrauliske systemer er analogt med enkle virkemidler, men de har den fordelen at trykket kan bli sendt gjennom tortuously buede linjer til flere steder på en gang.

Den hydrauliske jack er slik et hydraulisk system. En hydraulisk jekk er brukt til å løfte tunge belastninger, slik som de som brukes av auto mekanikerne til å løfte en bil. Det består av en inkompressible væske i et U-rør utstyrt med et bevegelig stempel på hver side. Den ene siden av U-rør er smalere enn andre., En liten styrke påføres over et lite område kan balansere en mye større kraft på den andre siden over et større område (Figur \(\PageIndex{3}\)).

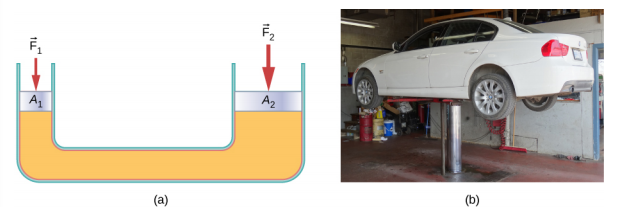
Fra Pascal ‘ s prinsipp, det kan vises at den kraften som er nødvendig for å løfte bilen er mindre enn vekten av bilen:

\

hvor F1 er kraften som brukes til å løfte bilen, A1 er den tverrsnitt av de mindre stempel, A2 er tverrsnittsområdet av de større stempel, og F2 er vekten av bilen.