.
학습 목표(s)
·정의 이벤트 결과,평가판,간단한 이벤트 샘플의 공간과 가능성을 산출하는 이벤트가 발생합니다.
·더 복잡한 결과에 대한 이벤트 확률을 계산합니다.
·확률을 포함하는 응용 프로그램을 해결합니다.
소개
확률 제공합의 측정을 가능성이 어떻게 그것이 뭔가가 발생합니다., 그것은 사이의 숫자이며 숫자 0 과 1 을 포함합니다. 분수,10 진수 또는 퍼센트로 쓸 수 있습니다.

번호를 선택하이 무작위로이 없다는 것을 의미한 특정 주문에서 그들이 선택됩니다. 많은 게임이 주사위 또는 스피너를 사용하여 무작위로 숫자를 생성합니다. 는 경우에 당신을 이해하는 방법을 확률을 계산할 수 있어 결정하는 방법에 대해 이러한 게임을 플레이하는 가능성의 다양한 결과입니다.,
정의
먼저 알아야 할 몇 가지 조건과 관련하여 확률이다. 확률로 작업 할 때 임의의 동작 또는 일련의 동작을 재판이라고합니다. 결과는 재판의 결과이며 이벤트는 특정 결과 모음입니다. 이벤트는 일반적으로 결과의 공통 특성을 사용하여 설명됩니다.이 언어를 적용하여 용어가 실제로 어떻게 작동하는지 살펴 보겠습니다. 일부 게임은 1 에서 6 까지 번호가 매겨진 6 면으로 다이를 굴릴 것을 요구합니다. (주사위는 다이의 복수형입니다.,)아래의 차트를 사용하여 시험 결과 및 이벤트에 대한 같은 게임:
통 컬렉션의 결과에서 중괄호 및 쉼표로 구분됩니다.간단한 이벤트는 하나의 결과 만있는 이벤트입니다. 작동하는 단 하나의 결과가 있기 때문에 1 을 굴리는 것은 간단한 이벤트 일 것입니다—1! 이벤트가 유효한 결과로 6 개만 포함하기 때문에 5 개 이상을 롤링하는 것도 간단한 이벤트가 될 것입니다. 복합 이벤트는 둘 이상의 결과가있는 이벤트입니다. 예를 들어,회전 중 하나는 여섯면 죽습니다,회전 짝수이 발생할 수 있는 하나의 세 가지 결과:2,4,6.,
경우 롤 육면 죽습니다 많은 시간이,당신은 기대하지 않는 모든 결과하는 일이 더 자주 다른 것보다(경우에는 공정한 죽습니다). 이와 같은 상황에서의 결과는 똑같이 가능성이 있다고합니다. 확률을 계산할 때 결과가 똑같이 가능성이있을 때를 인식하는 것이 매우 중요합니다. Die-rolling trial 의 각 결과가 똑같이 발생하므로 롤의 각 결과![]() 를 얻을 것으로 예상됩니다., 즉,당신이 기대하는
를 얻을 것으로 예상됩니다., 즉,당신이 기대하는![]() 의 롤을 수 1,
의 롤을 수 1,![]() 의 롤을 수 2,
의 롤을 수 2,![]() 의 롤 3 니다.
의 롤 3 니다.
회 전자는 아래 그림과 같이 각각 다른 색으로 채색 된 4 개의 동일한 부분으로 나뉩니다. 이 스피너가 회전하면 화살표가 색상 중 하나를 가리 킵니다. 결과는 똑같이 가능성이 있습니까?
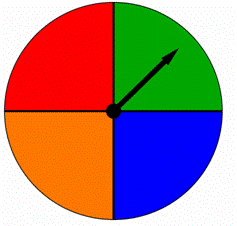
A)네 그들은 동등하게 높습니다.
B)아니오,그들은 똑같이 가능성이 없습니다.,
확률의 이벤트
건의 확률이 얼마나 자주 발생할 것으로 예상된다. 이는 샘플 공간의 크기에 대한 이벤트 공간의 크기의 비율입니다.먼저 샘플 공간의 크기를 결정해야합니다. 샘플 공간의 크기는 가능한 결과의 총 수입니다. 예를 들어 1 다이를 굴릴 때 샘플 공간은 1, 2, 3, 4, 5, 또는 6. 따라서 샘플 공간의 크기는 6 입니다.그런 다음 이벤트 공간의 크기를 결정해야합니다., 이벤트 공간은 관심있는 이벤트의 결과 수입니다. 3 보다 작은 숫자를 굴리는 이벤트 공간은 1 또는 2 입니다. 따라서 이벤트 공간의 크기는 2 입니다.
똑같이 가능성있는 결과의 경우,이벤트 E 의 확률은 p(E)로 쓸 수 있습니다.
![]()
|
예 |
||
|
문제 |
게임을 필요로 굴리면 죽습니다 번호는 1 에서 6., 짝수를 굴릴 확률은 얼마입니까? |
|
|
샘플의 공간= {1, 2, 3, 4, 5, 6}
이벤트 공간= {2, 4, 6} |
먼저 찾 샘플 공간 및 이벤트 공간입니다. 샘플 공간은 가능한 모든 결과이며 이벤트 공간은 이벤트의 결과입니다. 이 경우 이벤트는”짝수를 굴립니다.,” |
|
|
|
이후 결과를 똑같이 가능성이 확률의 이벤트는 비율의 이벤트 공간이를 샘플링하 공간이다., |
|
|
대답 |
P(짝수) = |
|
그것은 일반적인 실천과 확률과 같이 분수에서 일반적으로,단순화 가능성으로 가장 낮은 조건문을 위해 쉽게 만드는 대부분의 사람들이 감각을 얻을 수있는 좋은 방법입니다. 그렇게하지 않을 이유가없는 한,모든 최종 확률을 가장 낮은 용어로 표현하십시오.,
회 전자는 아래와 같이 각각 다른 색으로 채색 된 동일한 부분으로 나뉩니다., 가능성을 찾을 수 있 회전이나 녹색 파란색이 spinner:
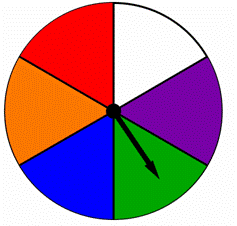
A)![]()
B)![]()
C) 2
D)6.
을 계산하는 방법을 찾기 샘플을 공간
가장 어려운 것은 계산에 확률이 될 수 있습을 찾는 샘플 크기는 공간이 있는 경우에 특히는 두 개 이상의 시험이다. 도움이 될 수있는 몇 가지 계산 방법이 있습니다.,
가장 먼저 살펴볼 것은 차트를 만드는 것입니다. 아래의 예에서 토리는 두 개의 동전을 뒤집고 있습니다. 그래서 샘플 공간을 신중하게 결정해야합니다. 다음 예제에 표시된 것과 같은 차트가 좋은 접근 방식입니다.
|
예 |
||||
|
문제 |
토리가 내리고 한 쌍의 동전을 주목할 필요 얼마나 많은 대칭의”머리”그녀를 가져옵니다. 그녀가 2 개의 머리를 뒤집을 확률은 얼마입니까?, 그녀가 단지 1 개의 머리를 뒤집을 확률은 얼마입니까?,15ecf6″>T |
T |
TT |
|
sample space: {HH, HT, TH, TT}
event space for 2 heads: {HH}
event space for 1 head: {HT, TH}
Create a chart to record the results of flipping the first coin, followed by the result of flipping the second coin.,
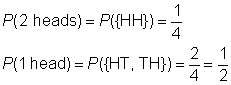
이후 결과를 똑같이 가능성이 확률의 이벤트는 비율의 이벤트 공간이를 샘플링하 공간이다.,
대답
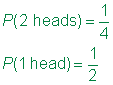
아래 예에서 샘플을 위한 공간토리는 단순한 하나만으로 죽어가는 유연성을 제공합니다. 그러나 James 가 two die 를 굴리고 있기 때문에 차트는 정보를 구성하는 데 도움이됩니다.,
|
예 |
||||||||
|
문제 |
토리연 여섯면 죽고 원하는 결과를 얻을 수의 1 개 또는 4. 제임스는 두 개의 6 면 주사위를 굴려 하나의 파란색과 하나의 빨간색으로 동시에 1 과 3 의 결과를 얻고 싶었습니다. 어떤 이벤트가 더 큰 확률을 가지고 있습니까?, |
|||||||
|
Tori’s sample space: {1, 2, 3, 4, 5, 6}
Tori’s event space: {1, 4}
Tori:
|
First, find the sample space and the event space for the two trials., 토리의 재판을 위해,이것은 간단합니다. 결과가 똑같이 가능하기 때문에 이벤트의 확률은 샘플 공간에 대한 이벤트 공간의 비율입니다.,316594724″> 6 |
6,1 |
6,2 |
6,3 |
6,4 |
6,5 |
6,6 |
|
James’ sample space has 36 outcomes.,이벤트 공간에는 2 개의 결과가 있습니다.두 개의 주사위를 굴리고 있기 때문에 제임스의 재판에는 그다지 분명하지 않습니다. 차트를 사용하여 가능성을 찾으십시오.
36 개의 결과가 있습니다. 이 중 1 과 3 을 모두 가진 2 가 있습니다.,
제임스: ![]()
이후 결과를 똑같이 가능성이 확률의 이벤트는 비율의 이벤트 공간이를 샘플링하 공간이다.
대답
토리의 이벤트가 더 확률입니다.,
사용할 수도 있습니다 나무에 다이어그램을 결정하는 샘플 공간입니다. 트리 다이어그램에는 각 이벤트에 대한 모든 가능한 결과에 대한 분기가 있습니다.
가장 세 바지(검정,흰색,녹색),네 개의 셔츠(녹색,백색,보라색,노란색),그리고 두 쌍의 신발(검은색 및 흰색). 얼마나 많은 다른 의상을 만들 수 있습니다? 바지에 대한 3 가지 선택,셔츠에 대한 4 가지 선택,신발에 대한 2 가지 선택이 있습니다., 트리 다이어그램의 경우 검정색의 경우 B,흰색의 경우 w,녹색의 경우 g,보라색의 경우 p 및 노란색의 경우 Y 를 사용합시다.
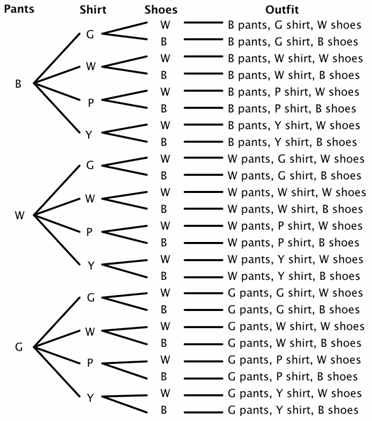
에서 볼 수 있는 나무도 있다는 가능한 24 의상(일부는 아마도 훌륭한 선택)샘플에 있는 공간입니다.
이제 몇 가지 확률 문제를 상당히 쉽게 해결할 수 있습니다. 예를 들어,눈을 감고 무작위로 선택하면 같은 색으로 바지와 신발을 선택할 확률은 얼마입니까? 바지와 신발이 일치하는 8 개의 의상이 있음을 알 수 있습니다.,
![]()
으로 봤을 때,평가판을 포함 하나 이상의 임의의 요소와 같은 튀기는 하나 이상의 동전이나 압연보다 더 하나 죽습니다,당신은 항상 필요로 하지 않을 식별하는 모든 결과에서 샘플을 공간을 계산하는 확률입니다. 결과의 수만하면됩니다.
기본 계산 원리는 나열하고 그들 모두를 계산하지 않고 결과의 수를 찾을 수있는 방법입니다.,
기본적인 계산을 원칙
경우 하나의 이벤트는 p 가능한 결과,다른 m 이벤트가 가능한 결과,다음의 총이있 p•m 를 위한 가능한 결과 두 개의 이벤트입니다.
예
·압연한 두 여섯면 주사위:각각의 다이에는 6 개 동등하게 높은 결과는,그래서 샘플을 공간은 6•6 36 동등하게 높은 결과입니다.
·내리고 세전:각 동전 2 동등하게 높은 결과는,그래서 샘플의 공간 2 • 2 • 2 8 동등하게 높은 결과입니다.,
·6 면 다이를 굴리고 동전을 뒤집기:샘플 공간은 6•2 또는 12 똑같이 가능성이있는 결과입니다.
사용할 수 있도록 기본적인 계산을 원칙을 얼마나 많은 의상에 있는 이전의 예입니다. 바지에 대한 3 가지 선택,셔츠에 대한 4 가지 선택,신발에 대한 2 가지 선택이 있습니다. 근본적인 계산 원리를 사용하면 다음과 같은 것들이 있습니다 4 • 3 • 2 =24 가지 의상.,
|
예 |
||
|
문제 |
배리에선 걷게 점심을 위한 모든 봉사자. 에서 각 부대에 넣는다. ·중 하나는 두 개의 샌드위치(땅콩 버터나 젤리,또는 터키와 치즈), ·하나의 세 칩(정기적인 감자 칩,구운 감자 칩,또는 옥수수 칩), ·한 조각의 열매(사과 또는 주황색)., 그는 가방에 무엇이 있는지 표시하는 것을 잊어 버렸습니다. 각 선택이 똑같이 가능성이 있다고 가정하면,Therese 가 얻는 가방이 땅콩 버터와 젤리 샌드위치와 사과를 보유 할 확률은 얼마입니까?, |
|
|
Size of sample space:
(number of sandwich choices) • (number of chip choices) • (number of fruit choices) = 2 • 3 • 2 = 12
|
First, use the Fundamental Counting Principle to find the size of the sample space., |
|
|
크기의 이벤트 공간이다.
(수 샌드위치에서 선택 이벤트) •(수 칩에서 선택 이벤트)•(수 의 과일을 선택에서 이벤트)= |
이벤트에 대한 공간에 따라 동일한 원리를 적용하고 있습니다. 이 경우 샌드위치와 관심있는 과일 한 조각 만 있지만 세 가지 유형의 칩 중 어느 것도 허용됩니다., |
|
|
대답 |
|
사용 비율을 찾기 위해 확률입니다. |
캐리 넘겼 네 개의 동전을 수의 꼬리를 가집니다. 정확히 하나의 꼬리를 얻는 네 가지 방법이 있습니다:HHHT,HHTH,HTHH 및 THHH. 캐리가 정확히 하나의 꼬리를 얻을 확률은 얼마입니까?,
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Summary
Probability helps you understand random, unpredictable situations where multiple outcomes are possible., 그것은 측정하는 가능성의 이벤트,그리고 그에 따라 달라의 비율이 가능한 이벤트와 결과는 경우에,그 모든 결과에 동등하게 높습니다.피>