공개 키 암호화

공개 키 암호화

과는 달리 대칭키 암호화 우리는 찾을 수없는 역사적 사용의 공개키 암호화 합니다. 그것은 비교적 새로운 개념입니다.

대칭 암호화한 단체와 같은 정부,군사,그리고 큰 금융기업에 참여했 분류 커뮤니케이션.,

의 확산과 함께 더욱 안전하지 않은 컴퓨터 네트워크에서 지난 몇 년 동안,진짜 필요를 느꼈을 사용하여 암호화에서 더 큰 규모입니다. 대칭 키는 키 관리에 직면 한 과제로 인해 실용적이지 않은 것으로 나타났습니다. 이것은 공개 키 암호 시스템을 야기했습니다.

프로세스의 암호화 및 복호화에서 묘사되는 다음 그림−

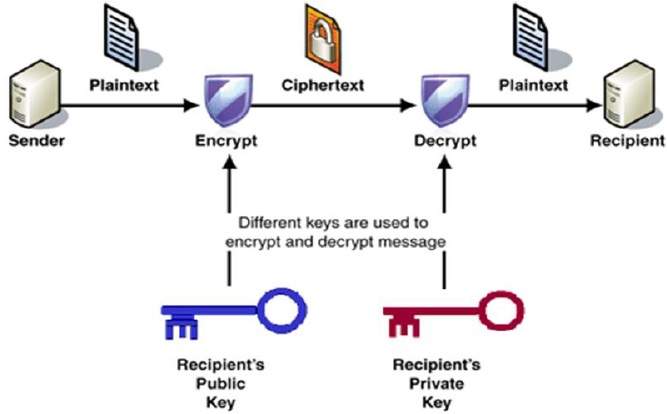
가장 중요한 특성의 공개 키 암호화 방식은−

• 서로 다른 키를 사용한 암호화 및 복호화합니다., 이것은 대칭 암호화 체계와 다른이 체계를 설정하는 속성입니다.

• 각 수신기는 일반적으로 그의 개인 키라고 불리는 고유 한 암호 해독 키를 보유합니다.

• 수신기는 자신의 공개 키라고 불리는 암호화 키를 게시해야합니다.

• 일부의 보증에 신뢰성을의 공용 키가 필요한 이 계획을 피하는 스푸핑여 적으로 수신기가 있습니다. 일반적으로,이러한 유형의 암호시스템을 포함한 신뢰할 수 있는 제삼자가 증명하는 특정한 공개 키를 그리고 특정 사용자 또는 엔티티만 있습니다.,

• 암호화 알고리즘을 충분히 복잡을 금지하는 공격자에 대한 추론 일반 텍스트에서 암호 및 암호화(public)키이다.

• 지만 민간과 공공의 열쇠는 관한 수학적으로,그것은 가능하지 않을 계산하는 개인 키에서 공용 키가 있습니다. 사실,모든 공개 키 암호 시스템의 지능적인 부분은 두 키 사이의 관계를 설계하는 데 있습니다.

세 가지 유형의 공개 키 암호화 체계가 있습니다., 우리는 다음 섹션에서 논의합니다-

RSA Cryptosystem

이 cryptosystem 은 초기 시스템 중 하나입니다. 그것은 오늘날에도 가장 많이 사용되는 암호 시스템으로 남아 있습니다. 이 시스템은 Ron Rivest,Adi Shamir 및 Len Adleman 의 세 학자에 의해 발명되었으며 따라서 RSA cryptosystem 으로 불립니다.

우리는 볼 것이 두 가지 측면의 RSA 암호시스템,첫째 세대의 키 쌍 둘째는 암호 해독 알고리즘이 있습니다.,

세대의 RSA 키 쌍

각 사람 또는 당사자가 소망에 참여하는 통신을 사용하여 암호화 요구를 생성하는 한 쌍의 키,즉 공개 키와 개체를 검색할 수 있습니다. 프로세스가 다음 세대에서 키의 설명 아래

• 생성 RSA 계수(n)

  • 를 선택하는 두 개의 큰 소수,p q.

  • Calculate n=p*q. 에 대한 강력한 깨지지 않는 암호화,보 n 수,일반적으로 최소한의 512 비트입니다.,

• 찾 파생 번호(e)

  • 수 e 해야 합이 1 보다 크고 보다 적은(p−1)(q−1)입니다.

  • 1 을 제외하고 e 와(p−1)(q−1)에 대한 공통 요인이 없어야합니다. 즉,두 개의 숫자 e 와(p–1)(q–1)는 coprime 입니다.

• 공개 키를 형성

  • 숫자 쌍(n,e)은 RSA 공개 키를 형성하고 공개됩니다.,

  • 흥미롭지만,n 부분의 공용 키에 어려움을 인수 분해시킨 큰 소수를 보장하는 공격자에서 찾을 수없는 유한 시간을 두 소수다(p&q)을 얻는 데 사용됩 n. 이것은 강도의 RSA.

• 를 생성한 개인 키

  • 개인 키 d 계산한 p,q,e. 를 위해 주어진 n e,거기에 고유 번호 d.

  • 수 d 역 e 모듈(p-1)(q–1)입니다., 즉,d 는(p-1)(q-1)보다 작은 수이므로 e 를 곱하면 1 모듈로(p-1)(q-1)와 같습니다.

  • 이 관계를 쓰는 수학적으로 다음과 같습니다−

ed = 1 mod (p − 1)(q − 1)

Extended 유클리드 알고리즘은 p,q,전자의 입력으로 제공 d 으로 출력됩니다.

실시예

rsa 키 쌍을 생성하는 예가 아래에 주어진다. (이해하기 쉽도록 여기에서 취한 소수 p&q 는 작은 값입니다. 실제로이 값은 매우 높습니다).,

• 두 소수가 p=7 이고 q=13 이되도록하십시오. 따라서 모듈러스 n=pq=7×13=91 입니다.

• select e=5,이는 5 와(p−1)(q 의 공통 요인 인 숫자가 없기 때문에 유효한 선택입니다− 1) = 6 × 12 = 72, 1 을 제외하고.

• 한 쌍의 번호(n,전자)=(91,5)형태로 공개 키를 사용할 수 있는 누군가 우리가 원하는을 보낼 수 있도록 우리에게 암호화된 메시지입니다.

• 확장 된 유클리드 알고리즘에 P=7,q=13 및 e=5 를 입력하십시오. 출력은 d=29 가됩니다.,

• 는지 확인하 d 계산이 정확해 컴퓨팅−

de = 29 × 5 = 145 = 1 mod 72

• 따라서,공개 키(91,5)개인 키(91,29).

암호화 및 복호화

키 쌍가 생성되고,프로세스의 암호화 및 복호화는 상대적으로 간단하고 계산이 쉽다.

흥미롭게도 rsa 는 대칭 키 암호화의 경우와 같이 비트 문자열에서 직접 작동하지 않습니다. 그것은 숫자 모듈로 n 에서 작동합니다.따라서 일반 텍스트를 n 보다 작은 일련의 숫자로 나타낼 필요가 있습니다.,

RSA 암호화

• 보낸 사람이 공개 키가(n,e)인 사람에게 문자 메시지를 보내려고한다고 가정합니다.

• 보낸 다음을 나타내는 일반 텍스트 등 일련의 숫자보다 n.

• 를 암호화하는 첫 번째 일반 텍스트 P 는 번호 모듈 n. 암호화 프로세스는 간단한 수학적으로 단계적으로−

C = Pe mod n

• 에 다른 단어,암호문 C 와 같은 일반 텍스트 P 곱하여 그 자체로 전자 회로 감소 모듈 n. 즉 C 는 또한 다수보다 적 n.,

• 반환을 우리의 주요 발생 예과반 P=10,우리는 암호문 C−

C = 105 mod 91

RSA 암호 해독

• 암호 해독 프로세스에 대한 RSA 은 또한 매우 간단합니다. 가정하자는 수신자의 공공-key pair(n,전자)을 받고 있는 암호문 C.

• Receiver 올 C 전원의 자신의 개인 키 d. 결과는 모듈 n 것이 일반 텍스트 P.,

Plaintext = Cd mod n

• 로 돌아 다시는 우리의 숫자를 들어, 암호문 C=82 것을 얻을 해독하는 10 번을 사용하여 개인 키 29−

Plaintext = 8229 mod 91 = 10

RSA 분석

의 보안 RSA 에 따라 달라의 강점을 두 가지 별도의 기능입니다. RSA cryptosystem 가장 인기있는 공개 키 cryptosystem 의 강도는 매우 큰 숫자를 인수 분해의 실제적인 어려움을 기반으로합니다.,

• 암호화 기능−간주되는 하나의 방법으로 변환하는 기능 일반 텍스트로 텍스트할 수 있습만 바꿔서의 지식으로 개인 키 d.

• 키를 세대의 어려움을 결정하는 개인에서 키 RSA public key 에 해당하는 양을 계수 n. 공격자에 따라서 사용할 수 없는 지식의 RSA 공개 키를 결정하는 RSA 개인 열쇠 그는할 수 있는 요인 n. 그것은 또한 한 가지 방법,기능에서 p&q 값을 계수 n 는 것은 쉽지만 반전이 가능하지 않습니다.,

이 두 기능 중 하나가 단방향이 아닌 것으로 입증되면 RSA 가 깨집니다. 사실,효율적으로 인수 분해를위한 기술이 개발되면 RSA 는 더 이상 안전하지 않을 것입니다.

의 강도는 RSA 암호화로 격렬하게 내려가 공격에 대한 경 p q 하지 않은 큰 소수 및/또는 선택한 공개 키 e 작은 번호입니다.

ElGamal Cryptosystem

RSA 와 함께 제안 된 다른 공개 키 암호 시스템이 있습니다. 그 중 많은 부분이 이산 로그 문제의 다른 버전을 기반으로합니다.,

타원 곡선 변형이라고하는 ElGamal cryptosystem 은 이산 로그 문제를 기반으로합니다. 파생하는 힘을 가정에서는 discrete logarithms 에서 찾을 수 없습니다 실용적인 기간에 대한 번호가 부여하는 동안,역동의 힘을 계산할 수 있습니다.

자 이동을 통해 간단한 버전의 ElGamal 작동하는 숫자와 함께 모듈 p. 의 경우 타원 곡선이 개,그에 따라 아주 다른 번호 시스템입니다.,

세대의 ElGamal 키 쌍

각 사용자의 ElGamal 암호시스템 키 쌍을 생성합을 통해 다음과 같습니다−

• 선택 큰 prime p. 일반적으로는 소수의 1024 2048 비트 길이 선택됩니다.

• 선택하는 발전소 g.

  • 이 번호는 1-p−1,수 없지만 얼마든지 가능합니다.

  • 그것은 발전기의 승 그룹의 정수 모듈 p. 이를 위해 각 정수 m co-prime p,정수가있다 k 등 gk=mod n.,

    예를 들어,3 은 그룹 5(Z5)의 생성기입니다= {1, 2, 3, 4}).

N	3n	3n 모 5
1	3	3
2	9	4
3	27	2
4	81	1

• 선택됩니다. 개인 키 x 는 1 보다 크고 p-1 보다 작은 숫자입니다.

• 공개 키의 컴퓨팅 부분., 값 y 에서 계산 매개변수를 p,g 및 개인 키 x 다음과 같습니다−

y = gx mod p

• 를 얻기 키입니다. ElGamal 공개 키는 세 가지 매개 변수(p,g,y)로 구성됩니다.

  예를 들어,p=17 이고 g=6 이라고 가정합니다(6 이 그룹 Z17 의 생성기임을 확인할 수 있음). 개인 키 x 는 1 보다 크고 71 보다 작은 숫자 일 수 있으므로 x=5 를 선택합니다. 값은 다음을 다음과 같이 계산됩니다−

y = 65 mod 17 = 7

• 따라서 개인 키 62 및 공개 키(17,6,7).,

암호화 및 복호화

세대의 ElGamal 가는 비교적 간단보다 해당하는 프로세스에 대한 RSA. 그러나 암호화 및 암호 해독은 RSA 보다 약간 복잡합니다.

ElGamal 암호화

가 보낸 사람에게 소원을 보낼 수반하는 사람 ElGamal 공개 키(p,g,y),그리−

• 보낸 사람을 나타내는 일반 텍스트 등 일련의 숫자는 모듈 p.

• 를 암호화하는 첫 번째 일반 텍스트 P 표시되는 수로 모듈 p., 암호화 프로세스를 구하는 암호문 C 은 다음과 같습니다−

  • 임의로 생성할 수 k;
  • 두 컴퓨팅 값 C1 과 C2,where−

C1 = gk mod pC2 = (P*yk) mod p

• 보내는 암호문 C 로 구성된 두 가지 별도의 값(C1,C2) 보냈다.,

• 을 참조하면 우리의 ElGamal 키 세대를 들어,위의 일반 텍스트 P=13 암호화는 다음과 같습니다−

  • 임의로 생성하수,말 k=10
  • 컴퓨팅 두 값 C1 과 C2, where−

C1 = 610 mod 17C2 = (13*710) mod 17 = 9

• 보내는 암호문 C=(C1,C2)=(15,9)고 했습니다.,

ElGamal 암호 해독

• 해독하는 암호문(C1,C2)을 이용하여 개인 키 x,다음과 같은 두 가지 단계는 취−

  • 컴퓨팅 모듈의 역(C1)x modulo p,(C1)-x,일반적으로 복호화 요소입니다.,

  • 얻 일반 텍스트를 사용하여 다음과 같은 공식−

C2 × (C1)-x mod p = Plaintext

• 에서 우리를 들어,암호문을 해독하는 C=(C1,C2)=(15,9)사용하여 개인 키 x=5, 암호 해독인 요소입니다.

15-5 mod 17 = 9

• 일반 텍스트 추출물 P=(9×9)모 17=13.

ElGamal 분석

에 ElGamal 시스템,각 사용자는 개인 키 x. 과는 세 가지 구성 요소의 공용 키 prime modulus p,발전기,g,공공 Y=gx 모 p., 엘가말의 강도는 이산 대수 문제의 난이도에 기초한다.

보안 키 크기는 일반적으로>1024 비트입니다. 오늘날에도 2048 비트 긴 키가 사용됩니다. 처리 속도 전면에서 Elgamal 은 매우 느리며 주로 키 인증 프로토콜에 사용됩니다. 높은 처리 효율로 인해 ElGamal 의 타원 곡선 변형이 점점 인기를 얻고 있습니다.,

Elliptic Curve Cryptography(ECC)

ECC(Elliptic Curve Cryptography)를 설명하기 위해 사용하는 용어의 암호화 툴 및 프로토콜의 보안에 따라 특별전형 대수 문제입니다. Numbers modulo p 를 사용하지 않습니다.

ECC 는 타원 곡선이라는 수학적 객체와 관련된 숫자 세트를 기반으로합니다. 숫자 모듈로 p 가있는 것처럼 이러한 숫자의 배수를 추가하고 계산하는 규칙이 있습니다.,

ECC 포함되어 있 개의 많은 암호화 방식이었다 처음에 설계를 위한 모듈식 번호와 같은 ElGamal 암호화하고 디지털 서명 알고리즘이 있습니다.

타원 곡선의 점에 적용 할 때 이산 로그 문제가 훨씬 더 어렵다고 믿어집니다. 이것은 숫자 모듈로 p 에서 타원 곡선의 점으로 전환하라는 메시지를 표시합니다. 또한 동등한 보안 수준을 얻을 수 있으로 짧은 키를 만약 우리가 사용하는 타원곡선 기반의 변형이 있습니다.,

짧은 키에 결과를 두 개의 혜택−

• 편의 키 management
• 효율적인 계산

이러한 혜택을 타원 곡선 기반 개의 암호화 방식을 매우 매력적인을 위한 응용 프로그램 컴퓨팅 리소스가 제한됩니다.

RSA 및 ElGamal 구성표–비교

다양한 측면에서 rsa 및 ElGamal 구성표를 간단히 비교해 보겠습니다.

RSA	ElGamal
암호화에 더 효율적입니다.	암호 해독에 더 효율적입니다.,
암호 해독에 덜 효율적입니다.	암호 해독에 더 효율적입니다.
특정 보안 수준의 경우 rsa 에서 긴 키가 필요합니다.	동일한 보안 수준의 경우 매우 짧은 키가 필요합니다.
널리 받아 들여지고 사용됩니다.	그것은 새로운 시장에서 매우 인기가 없습니다.