Probabilità
Obiettivi di apprendimento
· Definire evento, risultato, prova, evento semplice, spazio campione e calcolare la probabilità che si verifichi un evento.
· Calcola la probabilità di eventi per risultati più complessi.
· Risolvere applicazioni che coinvolgono probabilità.
Introduzione
La probabilità fornisce una misura di quanto sia probabile che qualcosa si verifichi., È un numero compreso tra i numeri 0 e 1. Può essere scritto come frazione, decimale o percentuale.

Scegliere i numeri in modo casuale significa che non esiste un ordine specifico in cui vengono scelti. Molti giochi usano dadi o filatori per generare numeri in modo casuale. Se capisci come calcolare le probabilità, puoi prendere decisioni ponderate su come giocare a questi giochi conoscendo la probabilità di vari risultati.,
Definizioni
Per prima cosa è necessario conoscere alcuni termini relativi alla probabilità. Quando si lavora con probabilità, un’azione casuale o una serie di azioni viene chiamata prova. Un risultato è il risultato di uno studio e un evento è una particolare raccolta di risultati. Gli eventi sono solitamente descritti utilizzando una caratteristica comune dei risultati.
Applichiamo questo linguaggio per vedere come funzionano i termini nella pratica. Alcuni giochi richiedono rotolamento un dado con sei lati, numerati da 1 a 6. (Dice è il plurale di die.,) La tabella seguente illustra l’uso di trial, outcome ed event per un gioco del genere:
Si noti che una raccolta di risultati viene messa tra parentesi graffe e separata da virgole.
Un evento semplice è un evento con un solo risultato. Rotolare un 1 sarebbe un evento semplice, perché c’è solo un risultato che funziona-1! Rotolare più di un 5 sarebbe anche un evento semplice, perché l’evento include solo 6 come risultato valido. Un evento composto è un evento con più di un risultato. Ad esempio, nel rotolamento di un dado a sei lati, il rotolamento di un numero pari potrebbe verificarsi con uno dei tre risultati: 2, 4 e 6.,
Quando tiri un dado a sei lati molte volte, non dovresti aspettarti che qualsiasi risultato accada più spesso di un altro (supponendo che si tratti di un dado equo). Si dice che i risultati in una situazione come questa siano ugualmente probabili. È molto importante riconoscere quando i risultati sono ugualmente probabili quando si calcola la probabilità. Poiché ogni risultato nella prova di laminazione è ugualmente probabile, ci si aspetterebbe di ottenere ogni risultato ![]() dei rotoli., Cioè, ti aspetteresti che
dei rotoli., Cioè, ti aspetteresti che ![]() dei rotoli sia 1,
dei rotoli sia 1, ![]() dei rotoli sia 2,
dei rotoli sia 2, ![]() dei rotoli sia 3 e così via.
dei rotoli sia 3 e così via.
Uno spinner è diviso in quattro parti uguali, ciascuna colorata con un colore diverso come mostrato di seguito. Quando questo filatore è filata, la freccia punta a uno dei colori. I risultati sono ugualmente probabili?
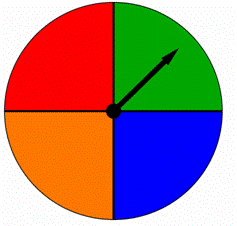
A) Sì, sono ugualmente probabili.
B) No, non sono ugualmente probabili.,
Probabilità di eventi
La probabilità di un evento è la frequenza con cui ci si aspetta che si verifichi. È il rapporto tra la dimensione dello spazio eventi e la dimensione dello spazio campione.
Innanzitutto, è necessario determinare la dimensione dello spazio campione. La dimensione dello spazio campione è il numero totale di possibili risultati. Ad esempio, quando si tira 1 dado, lo spazio del campione è 1, 2, 3, 4, 5, oppure 6. Quindi la dimensione dello spazio campione è 6.
Quindi è necessario determinare la dimensione dello spazio eventi., Lo spazio evento è il numero di risultati nell’evento che ti interessa. Lo spazio evento per il rotolamento di un numero inferiore a tre è 1 o 2. Quindi la dimensione dello spazio eventi è 2.
Per risultati altrettanto probabili, la probabilità di un evento E può essere scritta P(E).
![]()
|
Esempio |
||
|
Problema |
Un gioco richiede di rotolamento di un dado a sei facce numerate da 1 a 6., Qual è la probabilità di rotolare un numero pari? |
|
|
Esempio di spazio = {1, 2, 3, 4, 5, 6}
spazio per Eventi = {2, 4, 6} |
in Primo luogo, trovare l’esempio di spazio e spazio eventi. Lo spazio campione è tutti i possibili risultati e lo spazio evento è i risultati nell’evento. In questo caso, l’evento è ” rolling un numero pari.,” |
|
|
|
Dal momento che i risultati sono equiprobabili, la probabilità di un evento è il rapporto di spazi per eventi, per esempio di spazio., |
|
|
Risposta |
P(numero pari) = |
|
si tratta di una pratica comune con probabilità, come con le frazioni, in generale, per semplificare la probabilità in termini più dal momento che rende più facile per la maggior parte delle persone per ottenere un senso di come è grande. A meno che non ci sia motivo di non farlo, esprimere tutte le probabilità finali in termini più bassi.,
Uno spinner è diviso in parti uguali, ciascuna colorata con un colore diverso come mostrato di seguito., Trovare la probabilità di filatura blu o verde su questo spinner:
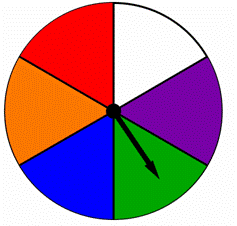
A) ![]()
B) ![]()
C) 2
D) 6
Metodi di Conteggio per trovare esempi di Spazi
La cosa più difficile per un calcolo di probabilità può essere quello di trovare la dimensione del campione di spazio, soprattutto se ci sono due o più prove. Ci sono diversi metodi di conteggio che possono aiutare.,
Il primo a guardare sta facendo un grafico. Nell’esempio seguente, Tori sta lanciando due monete. Quindi è necessario determinare attentamente lo spazio del campione. Un grafico come quello mostrato nell’esempio che segue è un buon approccio.
|
Esempio |
||||
|
Problema |
Tori sta lanciando un paio di monete e notando quanti lanci di “teste” si alza. Qual è la probabilità che lei capovolga 2 teste?, Qual è la probabilità che lei lanci solo 1 testa?,15ecf6”>T |
T |
TT |
|
sample space: {HH, HT, TH, TT}
event space for 2 heads: {HH}
event space for 1 head: {HT, TH}
Create a chart to record the results of flipping the first coin, followed by the result of flipping the second coin.,
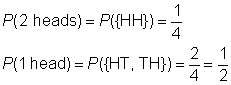
Dal momento che i risultati sono equiprobabili, la probabilità di un evento è il rapporto di spazi per eventi, per esempio di spazio.,
Risposta
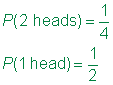
Nell’esempio riportato di seguito, il campione di spazio per i Tori è semplice come solo un dado è stato lanciato. Tuttavia, dal momento che James sta rotolando due muoiono, un grafico aiuta a organizzare le informazioni.,
|
Esempio |
||||||||
|
Problema |
Tori tirato un dado a sei facce e volevo ottenere un risultato di 1 o 4. James ha tirato due dadi a sei facce, uno blu e uno rosso, e voleva ottenere un risultato sia di un 1 che di un 3, allo stesso tempo. Quale evento ha una probabilità maggiore?, |
|||||||
|
Tori’s sample space: {1, 2, 3, 4, 5, 6}
Tori’s event space: {1, 4}
Tori:
|
First, find the sample space and the event space for the two trials., Per il processo di Tori, questo è semplice. Poiché i risultati sono ugualmente probabili, la probabilità dell’evento è il rapporto tra lo spazio degli eventi e lo spazio campione.,316594724″> 6 |
6,1 |
6,2 |
6,3 |
6,4 |
6,5 |
6,6 |
|
James’ sample space has 36 outcomes.,
Lo spazio eventi di James ha 2 risultati.
Non è così ovvio per il processo di James, dal momento che sta tirando due dadi. Utilizzare un grafico per trovare le possibilità.
Ci sono 36 risultati. Di questi, ce ne sono 2 che hanno sia 1 che 3.,
James: ![]()
Dal momento che i risultati sono equiprobabili, la probabilità di un evento è il rapporto di spazi per eventi, per esempio di spazio.
Risposta
L’evento di Tori ha una probabilità maggiore.,
È anche possibile utilizzare un diagramma ad albero per determinare lo spazio campione. Un diagramma ad albero ha un ramo per ogni risultato possibile per ogni evento.
Supponiamo che un armadio abbia tre paia di pantaloni (nero, bianco e verde), quattro camicie (verde, bianco, viola e giallo) e due paia di scarpe (bianco e nero). Quanti abiti diversi possono essere fatti? Ci sono 3 scelte per i pantaloni, 4 scelte per camicie, e 2 scelte per le scarpe., Per il nostro diagramma ad albero, usiamo B per il nero, W per il bianco, G per il verde, P per il viola e Y per il giallo.
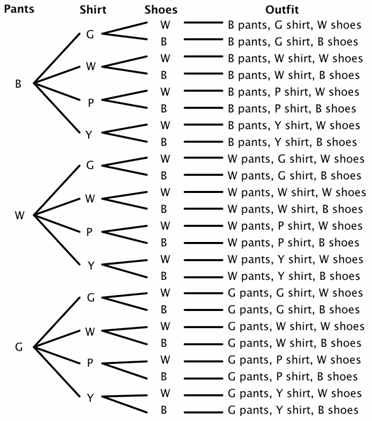
Puoi vedere dal diagramma ad albero che ci sono 24 possibili outfit (alcuni forse non grandi scelte) nello spazio campione.
Ora potresti risolvere abbastanza facilmente alcuni problemi di probabilità. Ad esempio, qual è la probabilità che se chiudi gli occhi e scegli a caso sceglieresti pantaloni e scarpe dello stesso colore? Si può vedere che ci sono 8 abiti in cui i pantaloni e le scarpe corrispondono.,
![]()
Come hai visto, quando una prova coinvolge più di un elemento casuale, come lanciare più di una moneta o rotolare più di un dado, non è sempre necessario identificare ogni risultato nello spazio campione per calcolare una probabilità. Hai solo bisogno del numero di risultati.
Il principio fondamentale di conteggio è un modo per trovare il numero di risultati senza elencare e contare ognuno di essi.,
Il principio fondamentale di conteggio
Se un evento ha p possibili risultati e un altro evento ha m possibili risultati, allora ci sono un totale di p • m possibili risultati per i due eventi.
Esempi
· Lanciare due dadi a sei facce: ogni dado ha 6 risultati ugualmente probabili, quindi lo spazio campione è 6 • 6 o 36 risultati altrettanto probabili.
· Lanciare tre monete: ogni moneta ha 2 risultati altrettanto probabili, quindi lo spazio del campione è 2 • 2 • 2 o 8 risultati altrettanto probabili.,
· Rotolare un dado a sei lati e lanciare una moneta: lo spazio del campione è 6 • 2 o 12 risultati altrettanto probabili.
Quindi potresti usare il principio di conteggio fondamentale per scoprire quanti abiti ci sono nell’esempio precedente. Ci sono 3 scelte per i pantaloni, 4 scelte per camicie, e 2 scelte per le scarpe. Usando il principio di conteggio fondamentale, hai 4 • 3 • 2 = 24 abiti diversi.,
|
Esempio |
||
|
Problema |
Barry i volontari di carità piedi per rendere il pranzo per tutti gli altri volontari. In ogni sacchetto si mette: · uno dei due panini al burro di arachidi e gelatina, o di tacchino e formaggio), · uno dei tre chip (regolare patatine fritte, patate al forno fiches, o chips di mais), · un frutto (una mela o un’arancia)., Ha dimenticato di segnare ciò che era nelle borse. Supponendo che ogni scelta è altrettanto probabile, qual è la probabilità che la borsa Therese ottiene detiene un burro di arachidi e gelatina panino e una mela?, |
|
|
Size of sample space:
(number of sandwich choices) • (number of chip choices) • (number of fruit choices) = 2 • 3 • 2 = 12
|
First, use the Fundamental Counting Principle to find the size of the sample space., |
|
|
Dimensione di spazi per eventi:
(numero di sandwich scelte a caso) • (numero di chip scelte a caso) • (numero di frutta scelte evento) = |
Per lo spazio eventi, seguire lo stesso principio. In questo caso, c’è solo un panino e un pezzo di frutta di interesse, ma uno dei tre tipi di chip è accettabile., |
|
|
Risposta |
|
Utilizzare il rapporto di trovare la probabilità. |
Carrie lancia quattro monete e conta il numero di code. Ci sono quattro modi per ottenere esattamente una coda: HHHT, HHTH, HTHH e THHH. Qual è la probabilità che Carrie ottiene esattamente una coda?,
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Summary
Probability helps you understand random, unpredictable situations where multiple outcomes are possible., È una misura della probabilità di un evento e dipende dal rapporto tra evento e possibili risultati, se tutti questi risultati sono ugualmente probabili.