Numeri immaginari

Un numero immaginario,al quadrato, dà un risultato negativo.

Prova

proviamo quadratura alcuni numeri per vedere se siamo in grado di ottenere un risultato negativo:

Senza fortuna! Sempre positivo, o zero.

Sembra che non possiamo moltiplicare un numero da solo per ottenere una risposta negativa …,

… ma immagina che ci sia un tale numero (chiamalo i per immaginario) che potrebbe fare questo: i × i = -1 Sarebbe utile, e cosa potremmo fare con esso?

Bene, prendendo la radice quadrata di entrambi i lati otteniamo questo:

il che significa che ho è la risposta per la radice quadrata di -1.

Che in realtà è molto utile perché …

Proviamo:

Hey! e ‘ stato interessante! La radice quadrata di -9 è semplicemente la radice quadrata di + 9, per i.,

In generale:

Finché teniamo quella piccola “i” lì per ricordarci che abbiamo ancora
bisogno di moltiplicare per √-1 siamo sicuri di continuare con la nostra soluzione!

Usando i

Interessante! Abbiamo usato un numero immaginario (5i) e abbiamo finito con una soluzione reale (-25).,

I numeri immaginari possono aiutarci a risolvere alcune equazioni:

Unità numero immaginario

La radice quadrata di meno uno √(-1) è il numero immaginario “unità”, l’equivalente di 1 per i numeri reali.

In matematica il simbolo per √(-1) è i per immaginario.

Puoi prendere la radice quadrata di -1?
Beh, posso!

Ma in elettronica usano j (perché “i” significa già corrente, e la lettera successiva dopo i è j).,

Examples of Imaginary Numbers

Imaginary Numbers are not “Imaginary”

Imaginary Numbers were once thought to be impossible, and so they were called “Imaginary” (to make fun of them).,

Ma poi le persone le hanno ricercate di più e hanno scoperto che erano effettivamente utili e importanti perché colmavano una lacuna in matematica … ma il nome “immaginario” si è bloccato.

Ed è anche così che è nato il nome “Numeri reali” (reale non è immaginario).,

Numeri Immaginari sono Utili

Numeri Complessi

numeri Immaginari diventare più utile se combinata con i numeri reali a fare i numeri complessi come 3+5i o 6 4i

Analizzatore di spettro

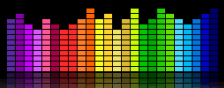
Quelle fresche display che si vede quando la musica è in riproduzione? Sì, i numeri complessi sono usati per calcolarli! Usando qualcosa chiamato “Trasformata di Fourier”.,

In effetti molte cose intelligenti possono essere fatte con il suono usando numeri complessi, come filtrare i suoni, sentire sussurri in mezzo alla folla e così via.

Fa parte di un soggetto chiamato “Elaborazione del segnale”.

Elettricità

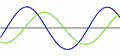
L’elettricità AC (corrente alternata) cambia tra positivo e negativo in un’onda sinusoidale.

Quando combiniamo due correnti AC potrebbero non corrispondere correttamente e può essere molto difficile capire la nuova corrente.,

Ma l’uso di numeri complessi rende molto più facile eseguire i calcoli.

E il risultato potrebbe avere una corrente” immaginaria”, ma può comunque farti del male!

Mandelbrot Set

Il bellissimo Mandelbrot Set (parte di esso è raffigurato qui) si basa su Numeri complessi.,

Equazione Quadratica

L’Equazione Quadratica, che ha molti usi,
può dare i risultati che includono numeri immaginari

Anche la Scienza, la meccanica Quantistica e la Relatività utilizzare i numeri complessi.

Proprietà interessante

Il numero immaginario unitario, i, ha una proprietà interessante., It “cycles” through 4 different values each time we multiply:

1 × i = i i × i = −1 −1 × i = −i −i × i = 1 Back to 1 again!,

So we have this: