la Crittografia a Chiave Pubblica

la Crittografia a Chiave Pubblica

a Differenza simmetrica crittografia a chiave, non troviamo storico uso della crittografia a chiave pubblica. È un concetto relativamente nuovo.

La crittografia simmetrica era adatta per organizzazioni come governi, militari e grandi società finanziarie coinvolte nella comunicazione classificata.,

Con la diffusione di reti di computer più non sicure negli ultimi decenni, è stata avvertita una vera necessità di utilizzare la crittografia su scala più ampia. La chiave simmetrica è risultata non pratica a causa delle sfide affrontate per la gestione delle chiavi. Ciò ha dato origine ai criptosistemi a chiave pubblica.

Il processo di crittografia e decrittografia è raffigurato nella seguente illustrazione −

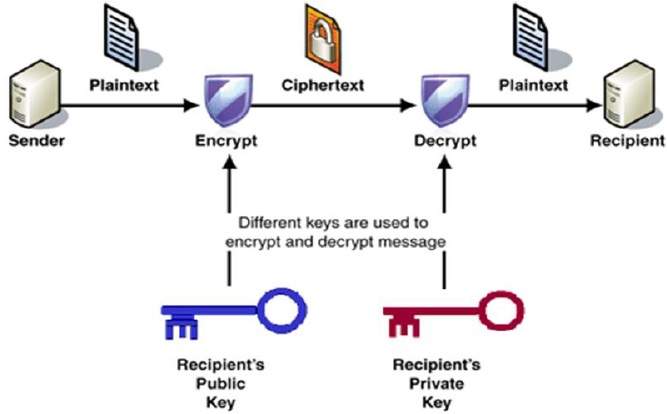
Le proprietà più importanti dello schema di crittografia a chiave pubblica sono −

• Diverse chiavi vengono utilizzate per la crittografia e la decrittografia., Questa è una proprietà che imposta questo schema diverso dallo schema di crittografia simmetrica.

• Ogni ricevitore possiede una chiave di decrittazione univoca, generalmente indicata come la sua chiave privata.

• Il ricevitore deve pubblicare una chiave di crittografia, denominata la sua chiave pubblica.

• È necessaria una certa garanzia dell’autenticità di una chiave pubblica in questo schema per evitare lo spoofing da parte dell’avversario come ricevitore. Generalmente, questo tipo di criptosistema coinvolge terze parti attendibili che certificano che una particolare chiave pubblica appartiene solo a una persona o entità specifica.,

• L’algoritmo di crittografia è abbastanza complesso da impedire all’utente malintenzionato di dedurre il testo in chiaro dal testo cifrato e dalla chiave di crittografia (pubblica).

• Sebbene le chiavi private e pubbliche siano correlate matematicamente, non è possibile calcolare la chiave privata dalla chiave pubblica. In effetti, una parte intelligente di qualsiasi criptosistema a chiave pubblica consiste nel progettare una relazione tra due chiavi.

Esistono tre tipi di schemi di crittografia a chiave pubblica., Li discutiamo nelle seguenti sezioni-

RSA Cryptosystem

Questo cryptosystem è uno del sistema iniziale. Rimane il cryptosystem più impiegato ancora oggi. Il sistema è stato inventato da tre studiosi Ron Rivest, Adi Shamir, e Len Adleman e quindi, è definito come RSA cryptosystem.

Vedremo due aspetti del cryptosystem RSA, in primo luogo la generazione di coppia di chiavi e in secondo luogo algoritmi di crittografia-decrittografia.,

Generazione di coppia di chiavi RSA

Ogni persona o una parte che desidera partecipare alla comunicazione utilizzando la crittografia deve generare una coppia di chiavi, vale a dire chiave pubblica e chiave privata. Il processo seguito nella generazione delle chiavi è descritto di seguito:

• Genera il modulo RSA (n)

  • Seleziona due numeri primi grandi, p e q.

  • Calcola n=p*q. Per una crittografia forte e infrangibile, sia n un numero elevato, in genere un minimo di 512 bit.,

• Trova il numero derivato (e)

  • Il numero e deve essere maggiore di 1 e minore di (p − 1)(q − 1).

  • Non ci deve essere un fattore comune per e e (p − 1)(q − 1) ad eccezione di 1. In altre parole due numeri e e (p-1) (q – 1) sono coprime.

• Forma la chiave pubblica

  • La coppia di numeri (n, e) forma la chiave pubblica RSA e viene resa pubblica.,

  • È interessante notare che, sebbene n faccia parte della chiave pubblica, la difficoltà nel fattorizzare un grande numero primo assicura che l’attaccante non possa trovare in tempo finito i due numeri primi (p& q) usati per ottenere n. Questa è la forza di RSA.

• Genera la chiave privata

  • La chiave privata d viene calcolata da p, q ed e. Per i dati n ed e, esiste un numero univoco d.

  • Il numero d è l’inverso di e modulo (p – 1)(q – 1)., Ciò significa che d è il numero inferiore a (p – 1) (q – 1) tale che quando moltiplicato per e, è uguale a 1 modulo(p – 1) (q – 1).

  • Questa relazione è scritta matematicamente come segue −

ed = 1 mod (p − 1)(q − 1)

L’algoritmo euclideo esteso prende p, q ed e come input e dà d come output.

Esempio

Di seguito è riportato un esempio di generazione della coppia di chiavi RSA. (Per facilità di comprensione, i numeri primi p& q presi qui sono piccoli valori. Praticamente, questi valori sono molto alti).,

• Lascia che due numeri primi siano p = 7 e q = 13. Quindi, modulo n = pq = 7 x 13 = 91.

• Seleziona e = 5, che è una scelta valida poiché non esiste un numero che sia un fattore comune di 5 e(p − 1) (q− 1) = 6 × 12 = 72, tranne 1.

• La coppia di numeri (n, e) = (91, 5) costituisce la chiave pubblica e può essere resa disponibile a chiunque desideri essere in grado di inviarci messaggi crittografati.

• Ingresso p = 7, q = 13, ed e = 5 per l’algoritmo Euclideo esteso. L’uscita sarà d = 29.,

• Controlla che la d calcolata sia corretta calcolando –

de = 29 × 5 = 145 = 1 mod 72

• Quindi, la chiave pubblica è (91, 5) e le chiavi private è (91, 29).

Crittografia e decrittografia

Una volta che la coppia di chiavi è stata generata, il processo di crittografia e decrittografia è relativamente semplice e computazionalmente facile.

È interessante notare che RSA non opera direttamente su stringhe di bit come nel caso della crittografia a chiave simmetrica. Opera su numeri modulo n. Quindi, è necessario rappresentare il testo in chiaro come una serie di numeri inferiori a n.,

Crittografia RSA

• Supponiamo che il mittente desideri inviare un messaggio di testo a qualcuno la cui chiave pubblica è (n, e).

• Il mittente, rappresenta il testo di riferimento, come una serie di numeri inferiori a n.

• Per crittografare il primo testo in chiaro P, che è un numero modulo n. Il processo di crittografia è semplice matematica passo −

C = Pe mod n

• In altre parole, il testo cifrato C è uguale al testo in chiaro P moltiplicato per se stesso e volte e poi ridotta modulo n. Questo significa che C è anche un numero inferiore a n.,

• Tornando al nostro esempio di generazione di chiavi con testo in chiaro P = 10, otteniamo il testo cifrato C −

C = 105 mod 91

RSA Decryption

• Anche il processo di decrittazione per RSA è molto semplice. Supponiamo che il ricevitore della coppia di chiavi pubbliche (n, e) abbia ricevuto un testo cifrato C.

• Il ricevitore solleva C alla potenza della sua chiave privata d. Il risultato modulo n sarà il testo in chiaro P.,

Plaintext = Cd mod n

• Ritornando al nostro esempio numerico, il testo cifrato C = 82 vorresti avere decifrato al numero 10 utilizzando la chiave privata 29 −

Plaintext = 8229 mod 91 = 10

RSA di Analisi

La sicurezza di RSA dipende dalla forza di due funzioni separate. Il cryptosystem RSA è più popolare forza di crittografia a chiave pubblica di cui si basa sulla difficoltà pratica di factoring i numeri molto grandi.,

• la Funzione di Crittografia − è considerato come una funzione di conversione di testo in chiaro in testo cifrato e può essere invertita solo con la conoscenza della chiave privata d.

• la Generazione di chiavi − La difficoltà di stabilire una chiave privata da una chiave pubblica RSA è equivalente al factoring modulo n. Un utente malintenzionato pertanto non sono in grado di utilizzare la conoscenza di una chiave pubblica RSA per determinare una chiave privata RSA a meno che il fattore di n. È anche un modo di funzione, che va da p & q i valori di a modulo n è facile, ma indietro non è possibile.,

Se una di queste due funzioni viene dimostrata non a senso unico, RSA verrà interrotta. Infatti, se viene sviluppata una tecnica per il factoring in modo efficiente, RSA non sarà più sicura.

La forza della crittografia RSA diminuisce drasticamente contro gli attacchi se il numero p e q non sono numeri primi grandi e/ o la chiave pubblica scelta e è un numero piccolo.

Elgamal Cryptosystem

Insieme a RSA, ci sono altri cryptosystems a chiave pubblica proposti. Molti di questi sono basati su diverse versioni del problema del logaritmo discreto.,

Il crittosistema ElGamal, chiamato Variante della curva ellittica, si basa sul problema del logaritmo discreto. Deriva la forza dal presupposto che i logaritmi discreti non possono essere trovati in un lasso di tempo pratico per un dato numero, mentre l’operazione inversa della potenza può essere calcolata in modo efficiente.

Passiamo attraverso una semplice versione di ElGamal che funziona con i numeri modulo p. Nel caso di varianti di curve ellittiche, si basa su sistemi numerici molto diversi.,

Generazione della coppia di chiavi ElGamal

Ogni utente di Elgamal cryptosystem genera la coppia di chiavi come segue −

• Scegliendo un grande primo p. Generalmente viene scelto un numero primo di 1024 a 2048 bit di lunghezza.

• Scegliere un elemento generatore g.

  • Questo numero deve essere compreso tra 1 e p − 1, ma non può essere un numero qualsiasi.

  • È un generatore del gruppo moltiplicativo di interi modulo p. Ciò significa che per ogni intero m co-primo a p, esiste un intero k tale che gk=a mod n.,

    Ad esempio, 3 è generatore del gruppo 5 (Z5 = {1, 2, 3, 4}).

N	3n	3n mod 5
1	3	3
2	9	4
3	27	2
4	81	1

• Scegliere la chiave privata. La chiave privata x è un numero qualsiasi più grande di 1 e più piccolo di p−1.

• Calcolo di una parte della chiave pubblica., Il valore y viene calcolato dai parametri p, g e la chiave privata x come segue −

y = gx mod p

• Ottenere la chiave pubblica. La chiave pubblica ElGamal consiste dei tre parametri (p, g, y).

  Per esempio, supponiamo che p = 17 e che g = 6, Si può confermare che 6 è un generatore del gruppo Z17. La chiave privata x può essere qualsiasi numero più grande di 1 e più piccolo di 71, quindi scegliamo x = 5. Il valore y viene quindi calcolato come segue −

y = 65 mod 17 = 7

• Quindi la chiave privata è 62 e la chiave pubblica è (17, 6, 7).,

Crittografia e decrittografia

La generazione di una coppia di chiavi ElGamal è relativamente più semplice del processo equivalente per RSA. Ma la crittografia e la decrittografia sono leggermente più complesse di RSA.

Cifratura ElGamal

Supponiamo che il mittente desidera inviare un testo in chiaro a qualcuno di cui ElGamal chiave pubblica è (p, g, y), quindi −

• Mittente rappresenta il testo di riferimento, come una serie di numeri di modulo p.

• Per crittografare il primo testo in chiaro P, che è rappresentato come un numero di modulo p., Il processo di crittografia per ottenere il testo cifrato C è il seguente:

  • Genera casualmente un numero k;
  • Calcola due valori C1 e C2, dove −

C1 = gk mod pC2 = (P*yk) mod p

• Invia il testo cifrato C, costituito dai due valori separati (C1, C2), inviati insieme.,

• Riferimento alla nostra ElGamal generazione della chiave di esempio di cui sopra, il testo in chiaro P = 13 è codificata come segue:

  • generare in modo Casuale un numero, diciamo k = 10
  • Calcolare i due valori di C1 e C2, dove

C1 = 610 mod 17C2 = (13*710) mod 17 = 9

• Invia il testo cifrato C = (C1, C2) = (15, 9).,

Decrittografia ElGamal

• Per decifrare il testo cifrato (C1, C2) utilizzando la chiave privata x, vengono eseguiti i seguenti due passaggi:

  • Calcolare l’inverso modulare di (C1)x modulo p, che è (C1) −x , generalmente indicato come fattore di decrittazione.,

  • Ottenere il testo in chiaro utilizzando la seguente formula −

C2 × (C1)-x mod p = Plaintext

• Nel nostro esempio, per decifrare il testo cifrato C = (C1, C2) = (15, 9) utilizzando la chiave privata x = 5, la decrittografia fattore

15-5 mod 17 = 9

• Estrarre il testo in chiaro P = (9 × 9) mod 17 = 13.

Analisi ElGamal

Nel sistema ElGamal, ogni utente ha una chiave privata x. e ha tre componenti della chiave pubblica − modulo primo p, generatore g e pubblico Y = gx mod p., La forza dell’ElGamal si basa sulla difficoltà del problema del logaritmo discreto.

La dimensione della chiave di sicurezza è generalmente> 1024 bit. Oggi vengono utilizzati anche 2048 bit di chiave lunga. Sul fronte della velocità di elaborazione, Elgamal è piuttosto lento, viene utilizzato principalmente per i protocolli di autenticazione chiave. A causa della maggiore efficienza di elaborazione, le varianti a curva ellittica di ElGamal stanno diventando sempre più popolari.,

Crittografia a curva ellittica (ECC)

Crittografia a curva ellittica (ECC) è un termine usato per descrivere una suite di strumenti e protocolli crittografici la cui sicurezza è basata su versioni speciali del problema del logaritmo discreto. Non utilizza numeri modulo p.

ECC si basa su insiemi di numeri associati a oggetti matematici chiamati curve ellittiche. Ci sono regole per aggiungere e calcolare multipli di questi numeri, proprio come ci sono per i numeri modulo p.,

ECC include varianti di molti schemi crittografici inizialmente progettati per numeri modulari come la crittografia ElGamal e l’algoritmo di firma digitale.

Si ritiene che il problema del logaritmo discreto sia molto più difficile quando applicato a punti su una curva ellittica. Ciò richiede il passaggio da numeri modulo p a punti su una curva ellittica. Anche un livello di sicurezza equivalente può essere ottenuto con chiavi più corte se usiamo varianti basate su curve ellittiche.,

Le chiavi più corte portano a due vantaggi:

• Facilità di gestione delle chiavi
• Calcolo efficiente

Questi vantaggi rendono le varianti dello schema di crittografia basate su curve ellittiche altamente attraenti per le applicazioni in cui le risorse di calcolo sono limitate.

Schemi RSA ed ElGamal – Un confronto

Confrontiamo brevemente gli schemi RSA ed ElGamal sui vari aspetti.

RSA	ElGamal
È più efficiente per la crittografia.	È più efficiente per la decrittografia.,
È meno efficiente per la decrittografia.	È più efficiente per la decrittografia.
Per un particolare livello di sicurezza, sono necessarie chiavi lunghe in RSA.	Per lo stesso livello di sicurezza, sono necessarie chiavi molto brevi.
È ampiamente accettato e utilizzato.	È nuovo e non molto popolare nel mercato.