Correlazionali Ricerca: Ricerca di Relazioni Tra le Variabili
al contrario di descrizione e di ricerca, che è stato progettato principalmente per fornire immagini statiche, correlazionali di ricerca prevede la misura di due o più variabili rilevanti e di una valutazione del rapporto tra tali variabili., Ad esempio, le variabili di altezza e peso sono sistematicamente correlate (correlate) perché le persone più alte generalmente pesano più delle persone più corte. Allo stesso modo, anche il tempo di studio e gli errori di memoria sono correlati, perché più tempo viene dato a una persona per studiare un elenco di parole, meno errori farà. Quando ci sono due variabili nel progetto di ricerca, una di esse è chiamata variabile predittiva e l’altra variabile di risultato., Il disegno di ricerca possono essere visualizzati come questo, dove la freccia curva rappresenta il previsto correlazione tra le due variabili:
la Figura 2.2.2

Un modo di organizzare i dati da un correlazionali studio con due variabili è di grafico i valori di ciascuna delle variabili misurate utilizzando un grafico a dispersione. Come si può vedere in Figura 2.10 “Esempi di grafici a dispersione”, un grafico a dispersione è un’immagine visiva della relazione tra due variabili., Un punto è tracciato per ogni individuo all’intersezione dei suoi punteggi per le due variabili. Quando l’associazione tra le variabili sul grafico a dispersione può essere facilmente approssimata con una linea retta, come nelle parti (a) e (b) della Figura 2.10 “Esempi di grafici a dispersione”, si dice che le variabili abbiano una relazione lineare.
Quando la linea retta indica che gli individui che hanno valori superiori alla media per una variabile tendono anche ad avere valori superiori alla media per l’altra variabile, come nella parte (a), la relazione è detta lineare positiva., Esempi di relazioni lineari positive includono quelli tra altezza e peso, tra istruzione e reddito e tra età e abilità matematiche nei bambini. In ogni caso le persone che ottengono un punteggio più alto su una delle variabili tendono anche a ottenere un punteggio più alto sull’altra variabile. Le relazioni lineari negative, al contrario, come mostrato nella parte (b), si verificano quando valori superiori alla media per una variabile tendono ad essere associati a valori inferiori alla media per l’altra variabile., Esempi di relazioni lineari negative includono quelli tra l’età di un bambino e il numero di pannolini che il bambino usa, e tra la pratica e gli errori commessi su un compito di apprendimento. In questi casi le persone che ottengono un punteggio più alto su una delle variabili tendono a ottenere un punteggio più basso sull’altra variabile.
Le relazioni tra variabili che non possono essere descritte con una linea retta sono note come relazioni non lineari. La parte (c) della Figura 2.10 “Esempi di grafici a dispersione” mostra un modello comune in cui la distribuzione dei punti è essenzialmente casuale., In questo caso non esiste alcuna relazione tra le due variabili e si dice che siano indipendenti. Le parti d) ed e) della figura 2.10 “Esempi di grafici a dispersione” mostrano modelli di associazione in cui, sebbene esista un’associazione, i punti non sono ben descritti da una singola linea retta. Ad esempio, la parte (d) mostra il tipo di relazione che si verifica frequentemente tra ansia e prestazioni., Gli aumenti dell’ansia da livelli bassi a moderati sono associati ad aumenti delle prestazioni, mentre gli aumenti dell’ansia da livelli moderati ad alti sono associati a diminuzioni delle prestazioni. Le relazioni che cambiano direzione e quindi non sono descritte da una singola linea retta sono chiamate relazioni curvilinee.
Figura 2.10 Esempi di grafici a Dispersione
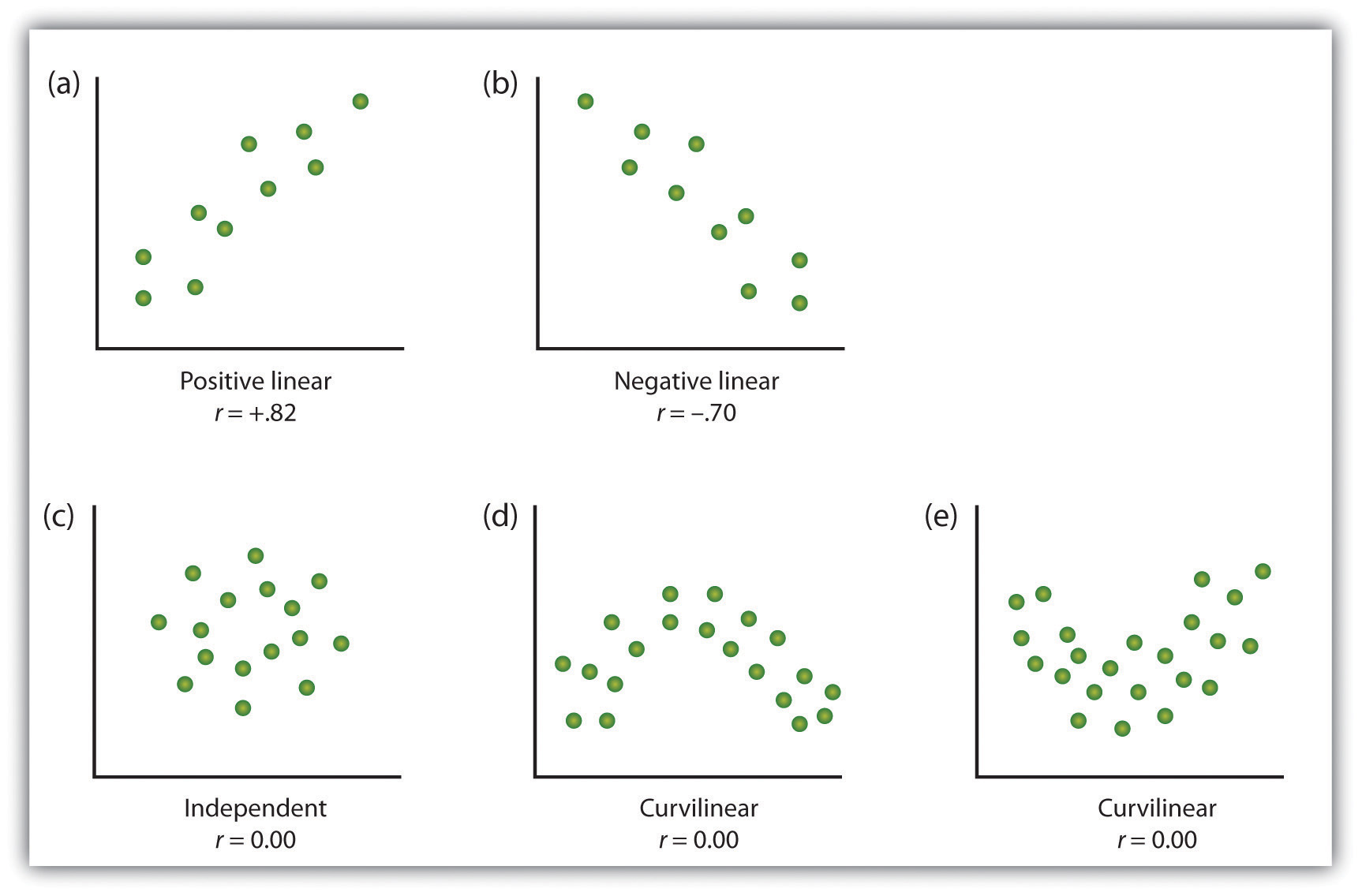
Alcuni esempi di relazioni tra due variabili, come mostrato nei grafici a dispersione., Si noti che il coefficiente di correlazione di Pearson (r) tra variabili che hanno relazioni curvilinee sarà probabilmente vicino a zero.
Adattato da Stangor, C. (2011). Metodi di ricerca per le scienze comportamentali (4a ed.). Vista sulle montagne, CA: Cengage.
La misura statistica più comune della forza delle relazioni lineari tra le variabili è il coefficiente di correlazione di Pearson, che è simboleggiato dalla lettera r. Il valore del coefficiente di correlazione varia da r = -1,00 a r = +1,00., La direzione della relazione lineare è indicata dal segno del coefficiente di correlazione. Valori positivi di r (come r = .54 o r = .67) indicano che la relazione è lineare positiva (cioè, il modello dei punti sul grafico a dispersione va dall’alto a sinistra in basso a destra), mentre i valori negativi di r (come r = –.30 o r = -.72) indicare relazioni lineari negative (cioè, i punti corrono dall’alto a sinistra in basso a destra). La forza della relazione lineare è indicizzata dalla distanza del coefficiente di correlazione da zero (il suo valore assoluto)., Ad esempio, r = -.54 è una relazione più forte di r = .30, e r = .72 è una relazione più forte di r = -.57. Poiché il coefficiente di correlazione di Pearson misura solo le relazioni lineari, le variabili che hanno relazioni curvilinee non sono ben descritte da r e la correlazione osservata sarà vicina allo zero.
È anche possibile studiare le relazioni tra più di due misure contemporaneamente., Un progetto di ricerca in cui più di una variabile predittiva viene utilizzata per prevedere una singola variabile di risultato viene analizzata attraverso la regressione multipla (Aiken & West, 1991). La regressione multipla è una tecnica statistica, basata su coefficienti di correlazione tra variabili, che consente di prevedere una singola variabile di risultato da più di una variabile predittiva. Ad esempio, la figura 2.11 “Previsione delle prestazioni del lavoro da tre variabili predittive” mostra un’analisi di regressione multipla in cui tre variabili predittive vengono utilizzate per prevedere un singolo risultato., L’uso di analisi di regressione multipla mostra un importante vantaggio dei progetti di ricerca correlazionale: possono essere utilizzati per fare previsioni sul punteggio probabile di una persona su una variabile di risultato (ad esempio, prestazioni lavorative) in base alla conoscenza di altre variabili.
Figura 2.11 Previsione di Prestazioni di Lavoro Da Tre Variabili Predittive
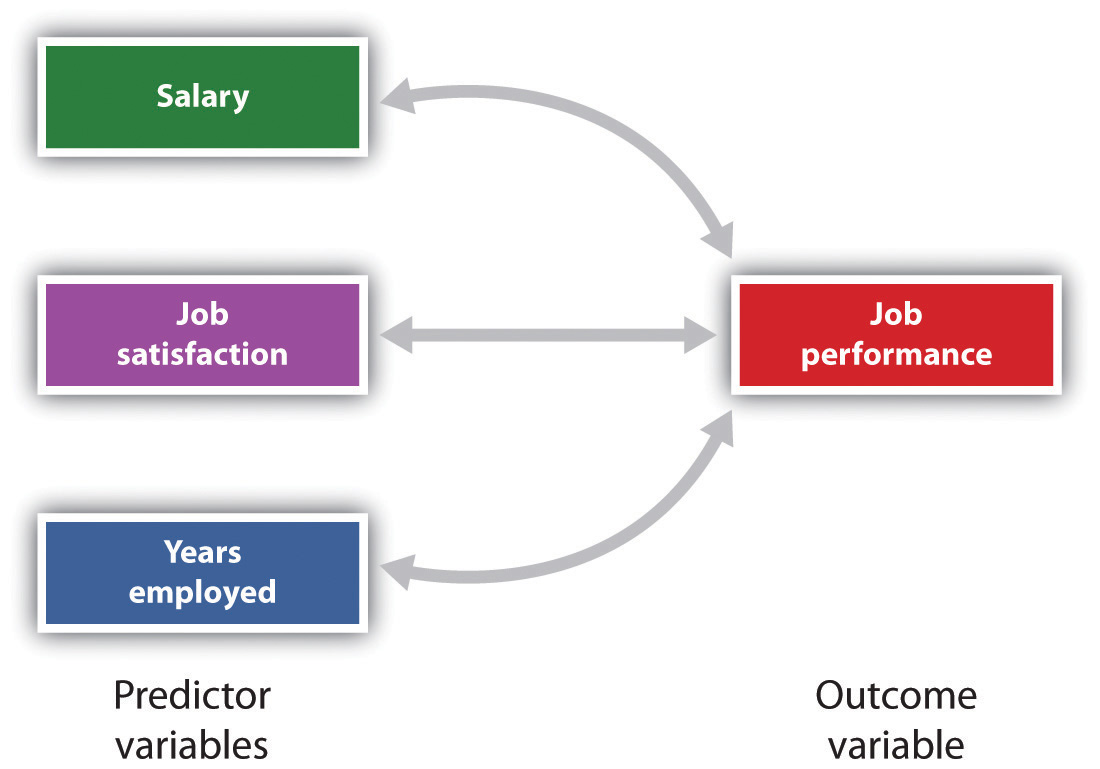
di regressione Multipla permette agli scienziati di prevedere i punteggi su una singola variabile di esito utilizzo di più di una variabile predittiva.,
Un’importante limitazione dei progetti di ricerca correlazionale è che non possono essere utilizzati per trarre conclusioni sulle relazioni causali tra le variabili misurate. Si consideri, ad esempio, un ricercatore che ha ipotizzato che la visualizzazione di comportamenti violenti causerà un aumento del gioco aggressivo nei bambini. Ha raccolto, da un campione di bambini di quarta elementare, una misura di quanti spettacoli televisivi violenti ogni bambino vede durante la settimana, così come una misura di come aggressivamente ogni bambino gioca nel parco giochi della scuola., Dai suoi dati raccolti, il ricercatore scopre una correlazione positiva tra le due variabili misurate.
Sebbene questa correlazione positiva sembri supportare l’ipotesi del ricercatore, non può essere presa per indicare che la visione di una televisione violenta causa un comportamento aggressivo. Anche se il ricercatore è tentati di supporre che la visione violenta televisione cause gioco aggressivo,
la Figura 2.2.2

ci sono altre possibilità., Una possibilità alternativa è che la direzione causale sia esattamente opposta a quella ipotizzata. Forse i bambini che si sono comportati in modo aggressivo a scuola sviluppare residuo entusiasmo che li porta a voler guardare spettacoli televisivi violenti a casa:
la Figura 2.2.2

anche se questa possibilità può sembrare meno probabile, non c’è modo di escludere la possibilità di una tale inversione di causalità sulla base di questa correlazione osservata., È anche possibile che sia causale indicazioni sono operativo e che le due variabili di causa-effetto:
la Figura 2.2.2

Ancora un’altra possibile spiegazione per la correlazione osservata è che è stato prodotto dalla presenza di un comune-causale variabile (noto anche come una terza variabile)., Una variabile causale comune è una variabile che non fa parte dell’ipotesi di ricerca ma che causa sia il predittore che la variabile di risultato e quindi produce la correlazione osservata tra di loro. Nel nostro esempio una potenziale variabile causale comune è lo stile di disciplina dei genitori dei bambini. I genitori che usano uno stile di disciplina dura e punitiva possono produrre bambini che amano guardare la televisione violenta e che si comportano in modo aggressivo rispetto ai bambini i cui genitori usano una disciplina meno dura:
Figura 2.2.,2
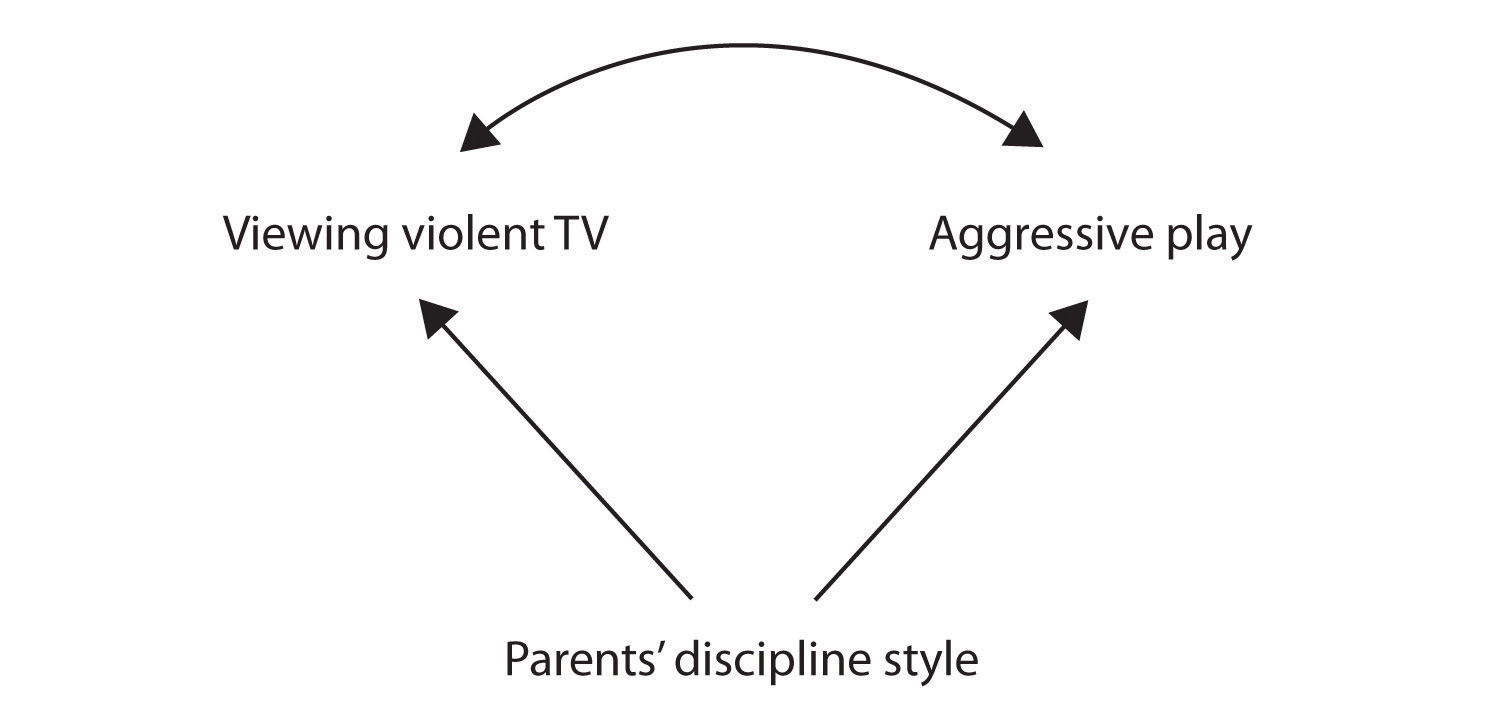
In questo caso, la visione della televisione e gioco aggressivo sarebbe correlato positivamente (come indicato dalla freccia curva tra di loro), anche se né l’uno causato altre ma erano entrambi causati dalla disciplina stile dei genitori (il dritto frecce). Quando il predittore e le variabili di risultato sono entrambi causati da una variabile causale comune, si dice che la relazione osservata tra di loro sia spuria., Una relazione spuria è una relazione tra due variabili in cui una variabile causale comune produce e “spiega” la relazione. Se gli effetti della variabile causale comune fossero tolti, o controllati per, la relazione tra il predittore e le variabili di risultato scomparirebbe. Nell’esempio la relazione tra aggressività e visione televisiva potrebbe essere spuria perché controllando l’effetto dello stile disciplinante dei genitori, la relazione tra visione televisiva e comportamento aggressivo potrebbe scomparire.,
Le variabili causali comuni nei progetti di ricerca correlazionale possono essere pensate come variabili “misteriose” perché, poiché non sono state misurate, la loro presenza e identità sono solitamente sconosciute al ricercatore. Poiché non è possibile misurare ogni variabile che potrebbe causare sia il predittore che le variabili di risultato, l’esistenza di una variabile causale comune sconosciuta è sempre una possibilità. Per questo motivo, ci rimane la limitazione di base della ricerca correlazionale: la correlazione non dimostra la causalità., E ‘ importante che quando si legge su progetti di ricerca correlazionali, si tiene a mente la possibilità di relazioni spurie, ed essere sicuri di interpretare i risultati in modo appropriato. Sebbene la ricerca correlazionale sia talvolta segnalata come dimostrazione di causalità senza alcuna menzione della possibilità di causalità inversa o variabili causali comuni, i consumatori informati della ricerca, come te, sono consapevoli di questi problemi interpretativi.
In sintesi, i progetti di ricerca correlazionale hanno sia punti di forza che limiti., Un punto di forza è che possono essere utilizzati quando la ricerca sperimentale non è possibile perché le variabili predittive non possono essere manipolate. I disegni correlazionali hanno anche il vantaggio di consentire al ricercatore di studiare il comportamento come avviene nella vita di tutti i giorni. E possiamo anche usare i disegni correlazionali per fare previsioni—per esempio, per prevedere dai punteggi sulla loro batteria di test il successo dei tirocinanti di lavoro durante una sessione di formazione. Ma non possiamo usare tali informazioni correlazionali per determinare se la formazione ha causato migliori prestazioni lavorative. Per questo, i ricercatori si basano su esperimenti.,