Související Výzkum: Hledání Vztahů Mezi Proměnnými
na rozdíl od deskriptivního výzkumu, který je určen především k zajištění statické obrázky, související výzkum zahrnuje měření dvou nebo více relevantních proměnných a posouzení vztahu mezi těmito proměnnými., Například proměnné výšky a hmotnosti jsou systematicky příbuzné (korelované), protože vyšší lidé obecně váží více než kratší lidi. Stejně tak souvisí i doba studia a chyby paměti, protože čím více času je člověk dán ke studiu seznamu slov, tím méně chyb udělá. Pokud jsou ve výzkumném návrhu dvě proměnné, jedna z nich se nazývá prediktorová proměnná a druhá výsledková proměnná., Výzkumný design může být zobrazil jako je tento, kde zahnutá šipka znázorňuje očekává, že korelace mezi dvěma proměnnými:
Obrázek 2.2.2

Jeden způsob, jak organizovat data ze související studie s dvou proměnných je graf hodnot jednotlivých měřených proměnných pomocí scatter plot. Jak můžete vidět na obrázku 2.10 „příklady rozptylových grafů“, rozptylový graf je vizuální obraz vztahu mezi dvěma proměnnými., Bod je vynesen pro každého jednotlivce v průsečíku jeho nebo její skóre pro dvě proměnné. Když lze asociaci mezi proměnnými na rozptylovém grafu snadno aproximovat přímkou, jako v částech (a) A (b) obrázku 2.10 „příklady rozptylových Parcel“, proměnné se říká, že mají lineární vztah.
Když přímka naznačuje, že jedinci, kteří mají nadprůměrné hodnoty jedné proměnné mají tendenci mít nad-průměrné hodnoty pro jiné proměnné, jako v části (a), vztah je řekl, aby byl pozitivní lineární., Příklady pozitivních lineárních vztahů zahrnují vztahy mezi výškou a hmotností, mezi vzděláním a příjmem a mezi věkem a matematickými schopnostmi u dětí. V každém případě lidé, kteří mají vyšší skóre na jedné z proměnných, mají také tendenci skóre vyšší na druhé proměnné. Negativní lineární vztahy, naopak, jak je znázorněno v části (b), se vyskytují, když nadprůměrné hodnoty pro jednu proměnnou mají tendenci být spojeny s podprůměrnými hodnotami pro druhou proměnnou., Příklady negativních lineárních vztahů zahrnují vztahy mezi věkem dítěte a počtem plenek, které dítě používá, a mezi praxí a chybami při učení. V těchto případech lidé, kteří skóre vyšší na jedné z proměnných mají tendenci skóre nižší na druhé proměnné.
Vztahy mezi proměnnými, které nelze popsat přímkou jsou známé jako nelineární vztahy. Část (c) obrázku 2.10 „příklady rozptylových Parcel“ ukazuje společný vzor, ve kterém je rozdělení bodů v podstatě náhodné., V tomto případě neexistuje žádný vztah mezi oběma proměnnými a říká se, že jsou nezávislé. Části (d) a (e) obrázku 2.10 „příklady rozptylových Parcel“ ukazují vzory sdružení, ve kterých, i když existuje sdružení, body nejsou dobře popsány jedinou přímkou. Například část (d) ukazuje Typ vztahu, který se často vyskytuje mezi úzkostí a výkonem., Zvýšení úzkosti z nízkých až středních úrovní je spojeno se zvýšením výkonu, zatímco zvýšení úzkosti ze středních až vysokých úrovní je spojeno se snížením výkonu. Vztahy, které se mění ve směru, a proto nejsou popsány jedinou přímkou, se nazývají křivočaré vztahy.
Obrázek 2.10 Příklady Scatter Pozemky,
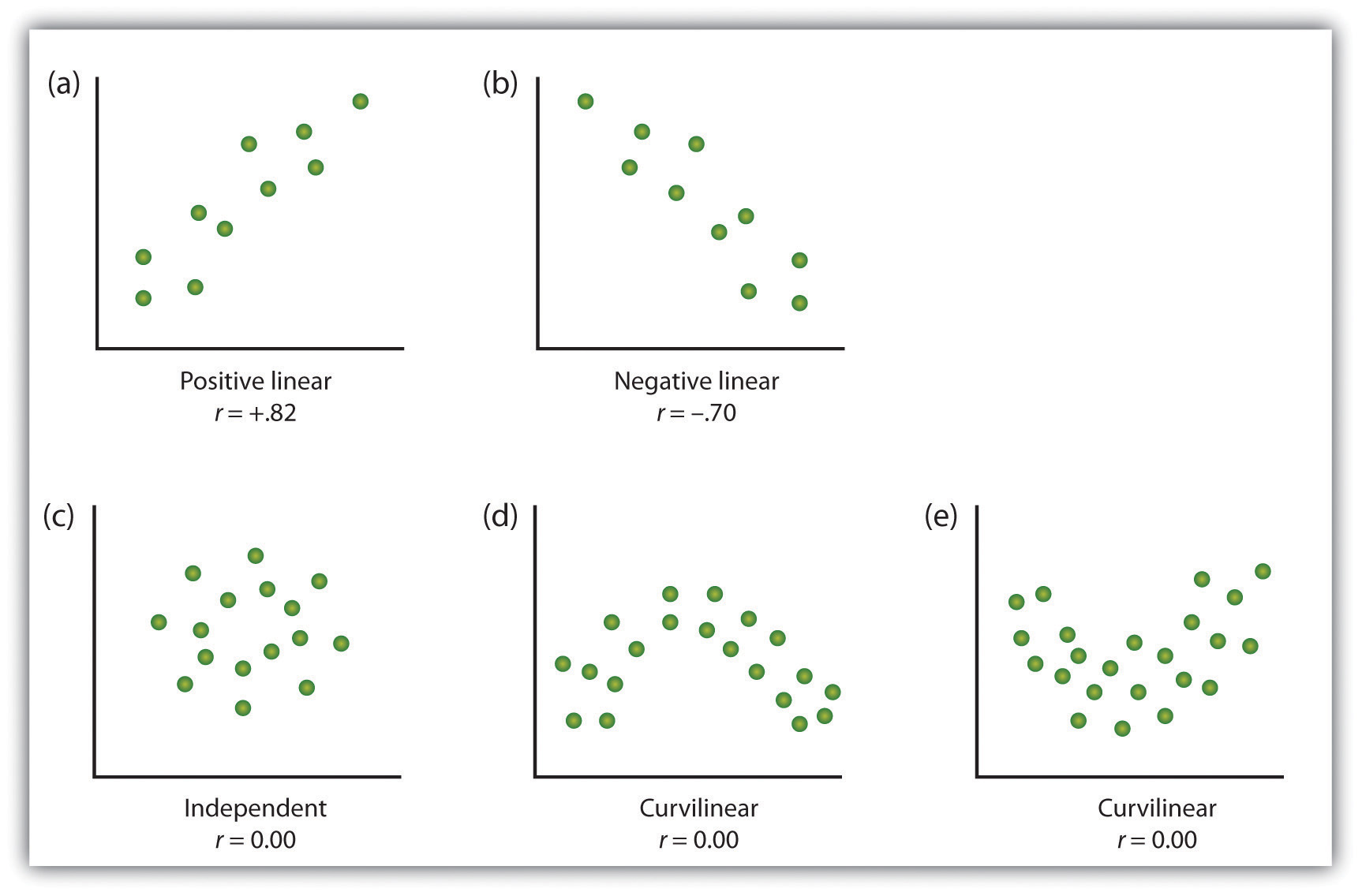
Některé příklady vztahů mezi dvěma proměnnými, jak je znázorněno na bodový pozemků., Všimněte si, že Pearsonův korelační koeficient (r) mezi proměnnými, které mají křivočaré vztahy, bude pravděpodobně blízko nuly.
upraveno od Stangor, C. (2011). Výzkumné metody behaviorálních věd (4.ed.). Mountain View, CA: Cengage.
nejběžnější statistické měření síly lineární vztahy mezi proměnnými je Pearsonův korelační koeficient, který je symbolizováno písmenem r. Hodnota korelačního koeficientu se pohybuje od r = -1.00 až r = +1.00., Směr lineárního vztahu je označen znaménkem korelačního koeficientu. Kladné hodnoty r (např. r = .54 nebo r = .67) ukazují, že vztah je pozitivní lineární (tj., vzor bodů na rozptylu pozemku běží od levého dolního do pravého horního rohu), zatímco záporné hodnoty r (například R = –.30 nebo r = –.72) uveďte negativní lineární vztahy (tj. tečky běží zleva nahoře vpravo dole). Síla lineárního vztahu je indexována vzdáleností korelačního koeficientu od nuly (jeho absolutní hodnota)., Například r = –.54 je silnější vztah než r = .30 a r = .72 je silnější vztah než r= -.57. Protože Pearsonův korelační koeficient měří pouze lineární vztahy, proměnné, které mají křivočaré vztahy, nejsou dobře popsány r a pozorovaná korelace bude téměř nulová.
je také možné studovat vztahy mezi více než dvěma opatřeními současně., Výzkumný design, ve kterém více než jedna prognostická proměnná je použit k předpovědět jeden výsledek proměnné analyzovány pomocí vícenásobné regrese (Aiken & West, 1991). Vícenásobná regrese je statistická technika založená na korelačních koeficientech mezi proměnnými, která umožňuje předpovídat proměnnou jednoho výsledku z více než jedné prediktorové proměnné. Například, Obrázek 2.11 „Predikce Pracovní Výkonnosti Ze Tří Prognostických Proměnných“ ukazuje vícenásobná regresní analýza, ve které tři prognostických proměnných se používají k předpovědět jeden výsledek., Použití vícenásobné regresní analýzy ukazuje důležitou výhodu korelačních výzkumných návrhů-lze je použít k předpovídání pravděpodobného skóre osoby na výsledkové proměnné (např.
Obrázek 2.11 Predikce pracovního Výkonu Od Tří Prognostických Proměnných,
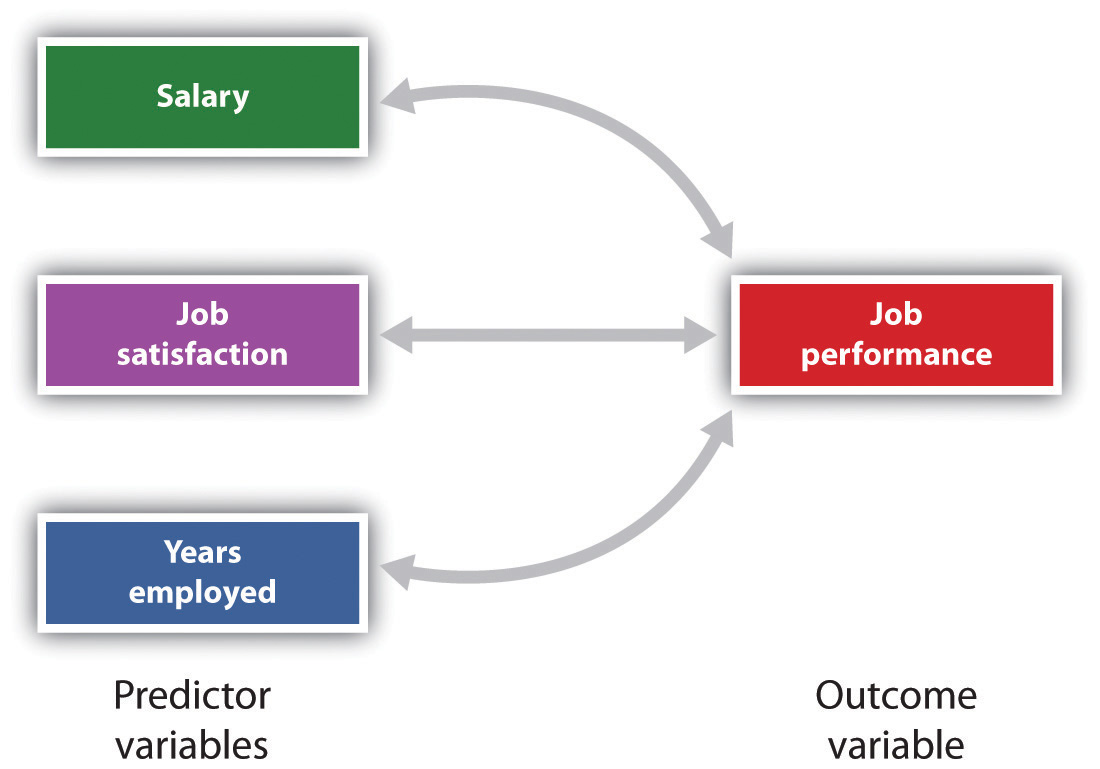
Vícenásobné regrese umožňuje vědcům předpovídat skóre na jediný výsledek proměnné pomocí více než jedna prognostická proměnná.,
důležitou omezení související výzkum vzorů je, že nemohou být použity k vyvození závěrů o kauzální vztahy mezi měřené proměnné. Zvažte například výzkumníka, který předpokládal, že prohlížení násilného chování způsobí zvýšenou agresivní hru u dětí. Shromáždil, ze vzorku čtvrté třídě děti, měřítkem toho, jak mnoho násilných televizních pořadů každé dítě výhledy během týdne, stejně jako měřítkem toho, jak agresivně každé dítě hraje na školním hřišti., Ze svých shromážděných dat výzkumník objevuje pozitivní korelaci mezi dvěma měřenými proměnnými.
přestože se zdá, že tato pozitivní korelace podporuje hypotézu výzkumníka, nelze ji považovat za důkaz, že sledování násilné televize způsobuje agresivní chování. I když výzkumník je v pokušení domnívat se, že sledování násilných televizních způsobuje agresivní hra,
Obrázek 2.2.2

existují i jiné možnosti., Jednou z alternativních možností je, že příčinný směr je přesně opačný než to, co bylo předpokládáno. Snad děti, které se chovají agresivně ve škole vytvořit reziduální vzrušení, které vede k chcete sledovat násilné televizní pořady doma:
Obrázek 2.2.2

i když tato možnost se může zdát méně pravděpodobné, neexistuje žádný způsob, jak vyloučit možnost, že takové reverzní příčinných souvislostí na základě tohoto pozorována korelace., Je také možné, že oba kauzální pokyny jsou provozní a dvou proměnných, protože každá další:
Obrázek 2.2.2

Ještě další možné vysvětlení pro pozorované korelace je, že to byl produkován přítomnost společného-kauzální proměnnou (také známý jako třetí proměnná)., Společná kauzální proměnná je proměnná, která není součástí výzkumné hypotézy, ale která způsobuje jak prediktor, tak výslednou proměnnou, a tak vytváří pozorovanou korelaci mezi nimi. V našem příkladu je potenciální společnou kauzální proměnnou disciplinární styl dětských rodičů. Rodiče, kteří používají drsné a represivní disciplína styl může produkovat děti, kteří rádi sledují násilné televizní a kteří se chovají agresivně ve srovnání s dětmi, jejichž rodiče používají méně tvrdá disciplína:
Obrázek 2.2.,2
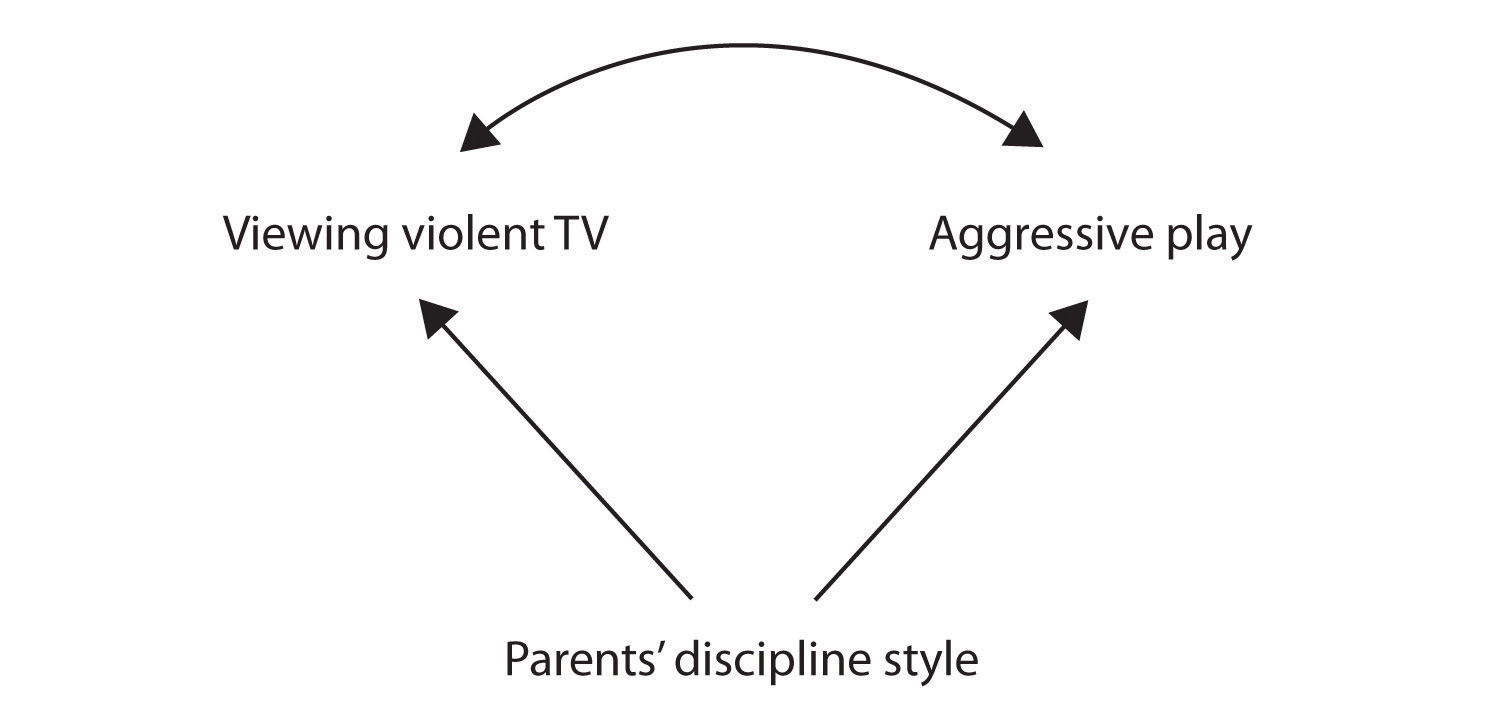
V tomto případě, sledování televize a agresivní hra by být pozitivně koreluje (jak je uvedeno na zakřivenou šipku mezi nimi), i když ani jedna způsobila druhou, ale obě byly způsobeny disciplíny styl rodičů (rovné šipky). Když prediktor a výsledek proměnné jsou způsobeny společné-kauzální proměnné, pozorovaný vztah mezi nimi je řekl, aby byl podvržený., Falešný vztah je vztah mezi dvěma proměnnými, ve kterých vzniká společná kauzální proměnná a „vysvětluje“ vztah. Pokud by byly účinky společné kauzální proměnné odebrány nebo kontrolovány, vztah mezi prediktorem a výslednými proměnnými by zmizel. V příkladu vztahu mezi agresí a sledování televize může být podvržený, protože kontrolou pro vliv rodičů ukáznit styl, vztah mezi sledování televize a agresivní chování by mohlo jít pryč.,
Common-kauzální proměnné v související výzkum vzorů může být myšlenka jako „tajemství“ proměnných, protože, jak oni nebyli změřit, jejich existence a identity jsou obvykle neznámého výzkumníka. Protože není možné měřit všechny proměnné, které by mohly způsobit oba prediktor a výsledek proměnné, na existenci neznámého společné-kauzální proměnné je vždy možnost. Z tohoto důvodu nám zůstává základní omezení korelačního výzkumu: korelace neprokazuje příčinnou souvislost., Je důležité, že když budete číst o související výzkumné projekty, mějte na paměti, možnost falešné vztahy, a ujistěte se, že interpretovat výsledky odpovídajícím způsobem. I když související výzkum je někdy hlášena jako prokázání příčinné souvislosti bez jakéhokoliv byla zmíněna možnost reverzní příčinných souvislostí, nebo společné-kauzální proměnné, informovaní spotřebitelé výzkumu, jako jste vy, jsou si vědomi těchto problémů výkladu.
stručně řečeno, návrhy korelačního výzkumu mají silné i omezené stránky., Jednou silou je, že mohou být použity, když experimentální výzkum není možný, protože proměnné prediktoru nelze manipulovat. Související vzory mají také tu výhodu, že umožňuje výzkumník studovat chování, jak se vyskytuje v každodenním životě. A můžeme použít také související vzory, aby se předpovědi—například, předvídat z výsledků na jejich baterie testů úspěch práce stážistů během tréninku. Nemůžeme však použít takové korelační informace k určení, zda školení způsobilo lepší pracovní výkon. Vědci se proto spoléhají na experimenty.,