Šifrování s Veřejným Klíčem

Kryptografie s Veřejným Klíčem

na Rozdíl od symetrické kryptografie, nenajdeme historické použití kryptografie veřejných klíčů. Jedná se o relativně nový koncept.

symetrická kryptografie byla vhodná pro organizace, jako jsou vlády, vojenské a velké finanční korporace, které se podílely na utajované komunikaci.,

s rozšířením více nezabezpečených počítačových sítí v posledních několika desetiletích byla pociťována skutečná potřeba používat kryptografii ve větším měřítku. Symetrický klíč byl shledán nepraktickým kvůli výzvám, kterým čelil pro klíčové řízení. To vedlo ke vzniku kryptosystémů veřejného klíče.

proces šifrování a dešifrování je znázorněn v následujícím obrázku −

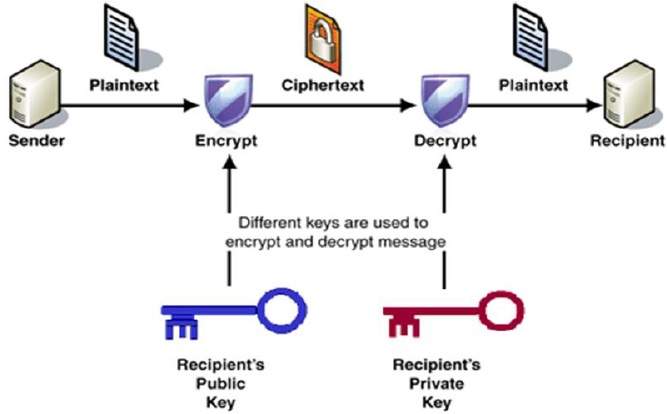
nejdůležitější vlastnosti veřejný klíč šifrovací schéma, jsou −

• Různé klíče pro šifrování a dešifrování., Toto je vlastnost, která nastavuje toto schéma jinak než symetrické šifrovací schéma.

• každý přijímač má jedinečný dešifrovací klíč, obvykle označovaný jako jeho soukromý klíč.

• přijímač musí publikovat šifrovací klíč, označovaný jako jeho veřejný klíč.

• v tomto schématu je zapotřebí určité ujištění o pravosti veřejného klíče, aby se zabránilo spoofingu protivníkem jako přijímačem. Obecně platí, že tento typ kryptosystému zahrnuje důvěryhodnou třetí stranu, která potvrzuje, že určitý veřejný klíč patří pouze konkrétní osobě nebo subjektu.,

• šifrovací algoritmus je natolik složitý, že útočníkovi zakáže odvodit prostý text z šifry a šifrovacího (veřejného) klíče.

• ačkoli soukromé a veřejné klíče jsou matematicky příbuzné, není možné vypočítat soukromý klíč z veřejného klíče. Ve skutečnosti je inteligentní součástí jakéhokoli kryptosystému veřejného klíče navrhování vztahu mezi dvěma klíči.

existují tři typy systémů šifrování veřejného klíče., Diskutujeme o nich v následujících sekcích-

RSA Cryptosystem

Tento kryptosystém je jedním z počátečních systémů. To zůstává nejvíce zaměstnán kryptosystém i dnes. Systém byl vynalezen třemi učenci Ron Rivest, Adi Shamir, a Len Adleman, a proto, to je nazýváno jako RSA cryptosystem.

uvidíme dva aspekty kryptosystému RSA, nejprve generaci dvojice klíčů a za druhé šifrování-dešifrovací algoritmy.,

generace dvojice klíčů RSA

každá osoba nebo strana, která se chce účastnit komunikace pomocí šifrování, musí vygenerovat pár klíčů, jmenovitě veřejný klíč a soukromý klíč. Proces následoval v generování klíčů je popsáno níže.

• Generování RSA modulus (n)

  • Vyberte dvě velká prvočísla p a q.

  • a spočítáme n=p*q. Pro silné nerozbitné šifrování, nechť n je velké číslo, obvykle minimálně 512 bitů.,

• Najděte odvozené číslo (e)

  • číslo e musí být větší než 1 a menší než (p − 1)(q − 1).

  • nesmí existovat žádný společný faktor pro e a (p − 1)(q − 1) s výjimkou 1. Jinými slovy, dvě čísla e a (p – 1)(q – 1) jsou koprime.

• tvoří veřejný klíč

  • dvojice čísel (n, e) tvoří veřejný klíč RSA a je zveřejněna.,

  • Zajímavé je, že když n je součástí veřejného klíče, potíže v factorizing velké prvočíslo zajišťuje, že útočník nemůže najít v konečných dobu dvou prvočísel (p & q) slouží k získání n. To je síla RSA.

• Vygenerovat soukromý klíč

  • Soukromý Klíč d se vypočte z p, q a e. Pro dané n a e, tam je jedinečné číslo d.

  • Číslo d je inverze e modulo (p – 1)(q – 1)., To znamená, že D je číslo menší než (p-1) (q – 1), takže když je vynásobeno e, rovná se 1 modulo(p – 1) (q – 1).

  • Tento vztah je napsáno matematicky takto −

ed = 1 mod (p − 1)(q − 1)

Rozšířený Euklidovský Algoritmus bere p, q, a, e jako vstup a dává d jako výstup.

příklad

níže je uveden příklad generování dvojice klíčů RSA. (Pro snadné pochopení jsou zde odebrané prvočísla p & q malé hodnoty. Prakticky jsou tyto hodnoty velmi vysoké).,

• nechte dvě prvočísla být p = 7 a q = 13. Modul n = pq = 7 x 13 = 91.

• Vyberte e = 5, což je platnou volbou, protože neexistuje číslo, které je společným faktorem 5 a (p − 1)(q− 1) = 6 × 12 = 72, s výjimkou 1.

• dvojice čísel (n, e) = (91, 5) tvoří veřejný klíč a může být zpřístupněna každému, komu chceme posílat šifrované zprávy.

• vstup p = 7, q = 13 A e = 5 do rozšířeného euklidovského algoritmu. Výstup bude d = 29.,

• ověřte, že d je vypočtena správná computing −

de = 29 × 5 = 145 = 1 mod 72

• Proto, veřejný klíč je (91, 5) a soukromý klíč je (91, 29).

šifrování a dešifrování

po vygenerování dvojice klíčů je proces šifrování a dešifrování relativně jednoduchý a výpočetně snadný.

zajímavé je, že RSA nepracuje přímo na řetězcích bitů jako v případě symetrického šifrování klíčů. Pracuje na číslech modulo n. proto je nutné reprezentovat prostý text jako řadu čísel méně než n.,

šifrování RSA

• Předpokládejme, že odesílatel chce poslat nějakou textovou zprávu někomu, jehož veřejný klíč je (n, e).

• odesílatel pak představuje otevřený text jako série čísla menší než n.

• K zašifrování první otevřený text P, což je číslo modulo n. Proces šifrování je jednoduché matematické krok jako −

C = Pe mod n

• jinými slovy šifrový text C je rovna holý P vynásobí sám e krát a pak se sníží modulo n. To znamená, že C je také číslo menší než n.,

• Návrat do našich Klíčových Generace, například s otevřený text P = 10, dostaneme šifrový C −

C = 105 mod 91

RSA Dešifrování

• proces dešifrování RSA je také velmi jednoduché. Předpokládejme, že příjemce veřejným klíčem dvojice (n, e) obdržel ciphertext C.

• Přijímač vyvolává C k síle jeho soukromý klíč d. Výsledek modulo n bude P. holého,

Plaintext = Cd mod n

• Vrací opět na náš číselný příklad, šifrový text C = 82 by se dešifrovat číslo 10 pomocí soukromého klíče 29 −

Plaintext = 8229 mod 91 = 10

RSA Analýzy

bezpečnost RSA závisí na silné dvě samostatné funkce. Kryptosystém RSA je nejoblíbenější kryptosystémovou silou veřejného klíče, která je založena na praktické obtížnosti factoringu velmi velkých čísel.,

• Funkce Šifrování − je považován za jednoho-způsob, funkce převodu textu na šifrový a může být zrušena pouze se znalostí soukromého klíče d.

• Generování Klíčů − obtížnost stanovení privátní klíč RSA veřejný klíč je ekvivalentní factoring modul n. Útočník tedy nemůže používat znalosti z RSA veřejného klíče k určení RSA soukromý klíč, pokud nemůže faktor n. To je také jeden způsob, jak fungovat, bude od p & q hodnoty modulo n, je snadné, ale opak je není možné.,

Pokud se některá z těchto dvou funkcí prokáže, že není jednosměrná, bude RSA přerušena. Ve skutečnosti, pokud je vyvinuta technika pro efektivní factoring, pak RSA již nebude bezpečná.

síla šifrování RSA drasticky klesá proti útokům, pokud číslo p A q nejsou velké prvočísla a/ nebo zvolený veřejný klíč e je malé číslo.

Elgamal Cryptosystem

spolu s RSA jsou navrženy další kryptosystémy veřejného klíče. Mnoho z nich je založeno na různých verzích Diskrétního problému logaritmu.,

Elgamal cryptosystem, nazývaný varianta eliptické křivky, je založen na diskrétním problému logaritmu. Odvozuje sílu z předpokladu, že diskrétní logaritmy nelze nalézt v praktickém časovém rámci pro dané číslo, zatímco inverzní provoz výkonu lze vypočítat efektivně.

projdeme jednoduchou verzí Elgamalu, která pracuje s čísly modulo p. V případě variant eliptické křivky je založena na zcela odlišných číselných systémech.,

Generace ElGamal Key Pair

Každý uživatel ElGamal šifrovacího systému generuje pár klíčů, přes takto −

• Výběr velké prvočíslo p. Obecně prvočíslo z 1024 na 2048 bitů délka je vybrán.

• volba prvku generátoru g.

  • toto číslo musí být mezi 1 a p-1, ale nemůže být žádné číslo.

  • To je generátor multiplikativní skupiny celých čísel modulo p. To znamená, že pro každé celé číslo m co-prvočíslo p, existuje celé číslo k takové, že gk=a mod n.,

    například 3 je generátor skupiny 5 (Z5 = {1, 2, 3, 4}).

N	3n	3n mod 5
1	3	3
2	9	4
3	27	2
4	81	1

• Volbu soukromý klíč. Soukromý klíč x je libovolné číslo větší než 1 a menší než p−1.

• výpočetní část veřejného klíče., Hodnota y je vypočítána z parametrů p, g a soukromý klíč x takto −

y = gx mod p

• Získání Veřejného klíče. Veřejný klíč ElGamal se skládá ze tří parametrů (p, g, y).

  například předpokládejme, že p = 17 a že g = 6 (lze potvrdit, že 6 je generátor skupiny Z17). Soukromý klíč x může být libovolné číslo větší než 1 a menší než 71, takže zvolíme x = 5. Hodnota y je pak vypočítán následovně −

y = 65 mod 17 = 7

• Tak soukromý klíč je 62 a veřejný klíč je (17, 6, 7).,

šifrování a dešifrování

generování páru klíčů ElGamal je poměrně jednodušší než ekvivalentní Proces pro RSA. Šifrování a dešifrování jsou však o něco složitější než RSA.

ElGamal Šifrování

Předpokládejme, že odesílatel chce odeslat ve formátu prostého textu, aby někdo, jehož ElGamal veřejný klíč (p, g, y), pak −

• Odesílatel představuje prostý text jako řadu čísel modulo p.

• K zašifrování první otevřený text P, který je reprezentován jako číslo modulo p., Proces šifrování získat šifrový text C je takto −

  • Náhodně generovat číslo k;
  • Compute dvě hodnoty C1 a C2, kde −

C1 = gk mod pC2 = (P*yk) mod p

• Odeslat ciphertext C, skládající se ze dvou oddělených hodnot (C1, C2), poslal spolu.,

• s Odkazem na náš ElGamal generování klíčů příklad uvedený výše, holý P = 13 je šifrována takto −

  • Náhodně generovat číslo k = 10
  • Vypočítat dvě hodnoty C1 a C2, kde −

C1 = 610 mod 17C2 = (13*710) mod 17 = 9

• Odeslat šifrový text C = (C1, C2) = (15, 9).,

ElGamal Dešifrování

• Chcete-li dešifrovat šifrovaná zpráva (C1, C2) pomocí soukromého klíče x, následující dva kroky −

  • Výpočet modulární inverze (C1)x modulo p, což je (C1)-x , obecně označované jako dešifrování faktor.,

  • Získat otevřený text pomocí následující vzorec.

C2 × (C1)-x mod p = Plaintext

• V našem příkladu, k dešifrování šifrový text C = (C1, C2) = (15, 9) pomocí soukromého klíče x = 5, dešifrování faktorem je,

15-5 mod 17 = 9

• Extrakt otevřený text P = (9 × 9) mod 17 = 13.

Elgamal Analysis

v systému ElGamal má každý uživatel soukromý klíč x. a má tři složky veřejného klíče-prime modulus p, generator g a public Y = Gx mod p., Síla Elgamalu je založena na obtížnosti diskrétního problému logaritmu.

velikost bezpečného klíče je obecně > 1024 bitů. Dnes se používá i 2048 bitů dlouhý klíč. Na přední straně rychlosti zpracování je Elgamal poměrně pomalý, používá se hlavně pro klíčové autentizační protokoly. Vzhledem k vyšší efektivitě zpracování jsou stále populárnější varianty eliptické křivky Elgamalu.,

Elliptic Curve Cryptography (ECC)

Elliptic Curve Cryptography (ECC) je termín používaný k popisu sadu kryptografických nástrojů a protokolů, jejichž bezpečnost je založena na speciální verzí problém diskrétního logaritmu. Nepoužívá čísla modulo p.

ECC je na základě sady čísel, které jsou spojeny s matematickými objekty, tzv. eliptické křivky. Existují pravidla pro přidávání a výpočet násobků těchto čísel, stejně jako pro čísla modulo p.,

ECC obsahuje varianty mnoha kryptografických schémat, které byly původně navrženy pro modulární čísla, jako je šifrování ElGamal a algoritmus digitálního podpisu.

předpokládá se, že diskrétní problém logaritmu je mnohem těžší, když je aplikován na body na eliptické křivce. To vyzve k přechodu z čísel modulo p na body na eliptické křivce. Také ekvivalentní úroveň zabezpečení lze získat s kratšími klávesami, pokud použijeme varianty založené na eliptické křivce.,

kratší klíče následek dvě výhody −

• Snadnost správy klíčů
• Efektivní výpočet

Tyto výhody, aby eliptické křivky založené variant šifrovací schéma vysoce atraktivní pro aplikace, kde se výpočetní zdroje jsou omezené.

schémata RSA a ElGamal-srovnání

stručně porovnejme schémata RSA a ElGamal o různých aspektech.

RSA	ElGamal
je účinnější pro šifrování.	je účinnější pro dešifrování.,
je méně efektivní pro dešifrování.	je účinnější pro dešifrování.
pro určitou úroveň zabezpečení jsou v RSA vyžadovány dlouhé klíče.	pro stejnou úroveň zabezpečení jsou vyžadovány velmi krátké klíče.
je široce přijímán a používán.	je to nové a není příliš populární na trhu.