Chcete-li použít referenční úhel kalkulačka, stačí zadat libovolný úhel v úhel box najít své referenční úhel, což je ostrý úhel, který odpovídá úhlu vstoupil. Kalkulačka automaticky použije pravidla, která si prohlédneme níže.
co je vlastně referenční úhel?
Představte si rovinu souřadnic. Řekněme, že chceme nakreslit úhel, který je v našem letadle 144°., Začínáme na pravé straně osy x, kde jsou tři hodiny na hodinách. Otáčíme proti směru hodinových ručiček, což začíná pohybem nahoru. Pokračujeme kolem bodu 90° (horní část osy y), dokud se nedostaneme na 144°. Nakreslíme paprsek od původu, který je středem roviny, do tohoto bodu. Nyní máme paprsek, který nazýváme koncovou stranou. Ale musíme nakreslit ještě jeden paprsek, abychom vytvořili úhel. V tuto chvíli máme na výběr. Náš druhý paprsek musí být na x-ose. Pokud ji nakreslíme z původu na pravou stranu, nakreslíme úhel, který měří 144°., Pokud ji nakreslíme doleva, nakreslíme úhel, který měří 36°. Tento druhý úhel je referenční úhel. Je to vždy menší ze dvou úhlů, bude vždy menší nebo rovno 90°, a to bude vždy pozitivní. Zde je animace, která ukazuje referenční úhel pro čtyři různé úhly, z nichž každý je v jiném kvadrantu. Všimněte si, jak je druhý paprsek vždy na ose x.
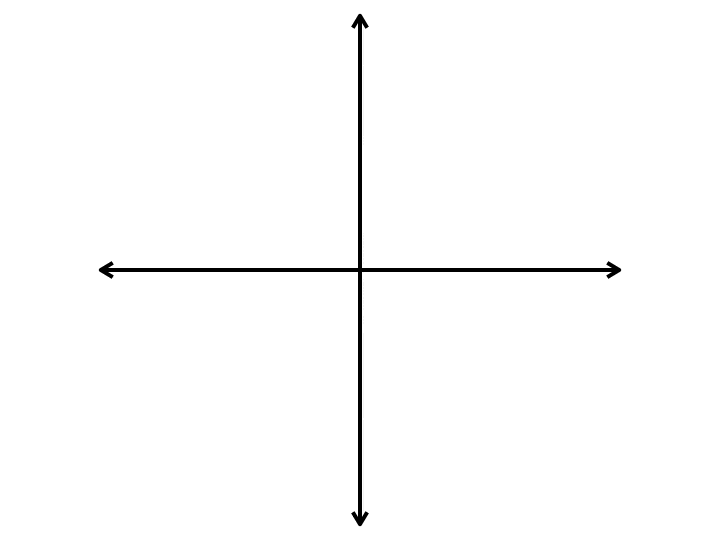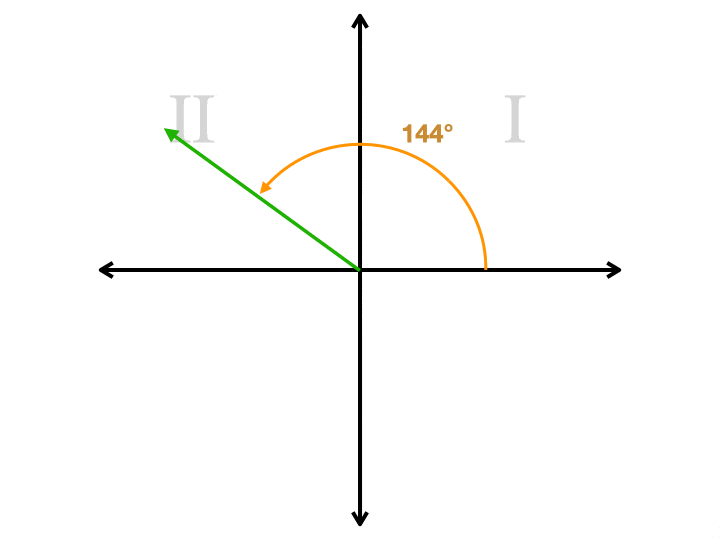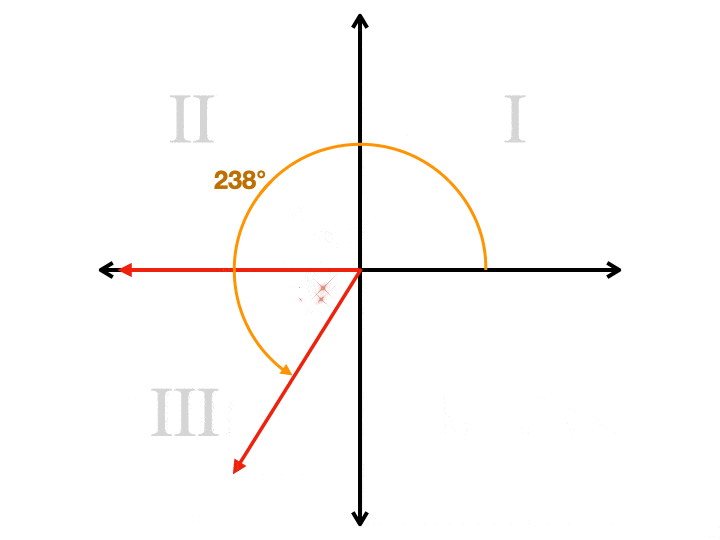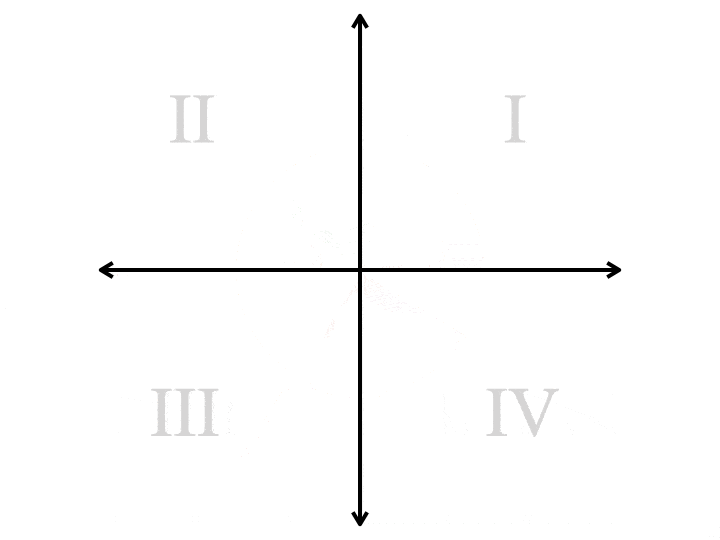
jak je užitečný referenční úhel?
referenční úhel má vždy stejné hodnoty funkce trig jako původní úhel. Všimněte si tam hodnot slov., Značka nemusí být stejná,ale hodnota bude vždy. To je užitečné pro běžné úhly jako 45° a 60° , se kterými se setkáme znovu a znovu. Jakmile známe jejich sinus, kosinus a tangentní hodnoty, známe také hodnoty pro jakýkoli úhel, jehož referenční úhel je také 45° nebo 60°. Jako na znamení, pamatujte si, že Sinus je kladná v 1. a 2. kvadrantu a Kosinus je kladná v 1. a 4. kvadrantu.
jak najdeme referenční úhel bez kalkulačky?
jak najdeme referenční úhel, závisí na kvadrantu koncové strany.,
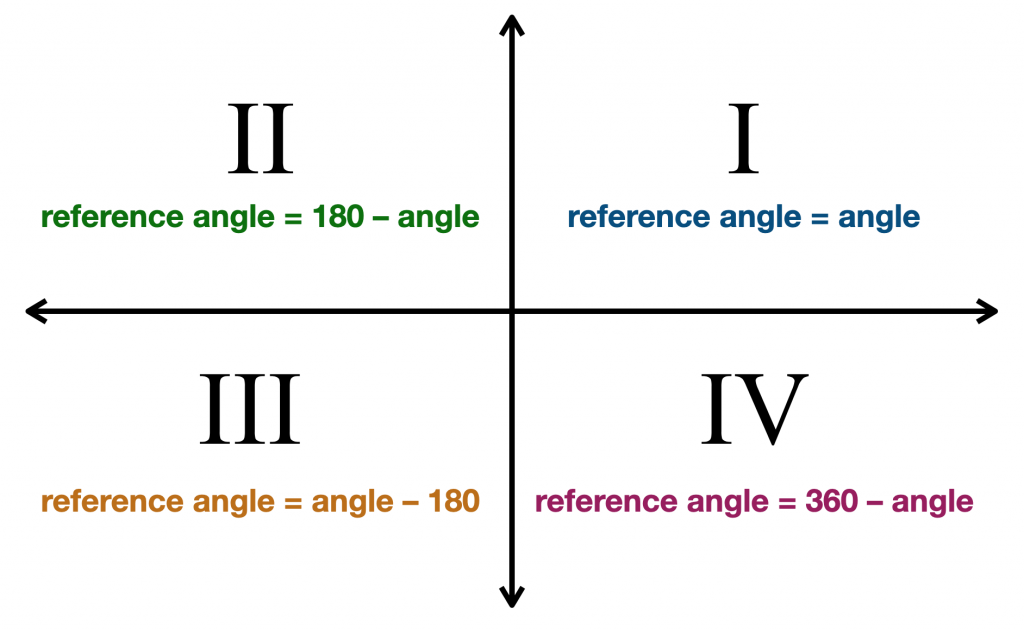
když je koncová strana v prvním kvadrantu (úhly od 0° do 90°), náš referenční úhel je stejný jako náš daný úhel. To dává smysl, protože všechny úhly v prvním kvadrantu jsou menší než 90°. Takže pokud je náš daný úhel 33°, pak je jeho referenční úhel také 33°.
když je koncová strana ve druhém kvadrantu (úhly od 90° do 180°), náš referenční úhel je 180° minus náš daný úhel. Takže pokud je náš daný úhel 110°, pak jeho referenční úhel je 180° – 110° = 70°.,
když je koncová strana ve třetím kvadrantu (úhly od 180° do 270°), náš referenční úhel je náš daný úhel minus 180°. Pokud je tedy náš daný úhel 214°, pak je jeho referenční úhel 214° – 180° = 34°.
když je koncová strana ve čtvrtém kvadrantu (úhly od 270° do 360°), náš referenční úhel je 360° minus náš daný úhel. Pokud je tedy náš daný úhel 332°, pak je jeho referenční úhel 360° – 332° = 28°.
co když je náš úhel větší než 360°?,
když je úhel větší než 360°, znamená to, že se otočil celou cestu kolem roviny souřadnic a pokračoval dál. Abychom našli jeho referenční úhel, musíme nejprve najít jeho odpovídající úhel mezi 0° a 360°. To je snadné. Jen od něj odečteme 360, dokud nebude pod 360. Například, pokud je náš úhel 544°, odečteme od něj 360°, abychom získali 184° (544° – 360° = 184°). Nyní bychom si všimli, že je ve třetím kvadrantu, takže bychom od něj odečetli 180°, abychom zjistili, že náš referenční úhel je 4°.
co když je náš úhel záporný?,
když je úhel záporný, přesuneme se opačným směrem, abychom našli naši koncovou stranu. To znamená, že se při kreslení pohybujeme ve směru hodinových ručiček namísto proti směru hodinových ručiček. Nebo to můžeme vypočítat jednoduše přidáním na 360°. Například, pokud je náš daný úhel -110°, pak bychom jej přidali na 360°, abychom našli náš kladný úhel 250° (-110° + 360° = 250°). Teď bychom museli vidět, že jsme ve třetím kvadrantu a použít toto pravidlo, abychom našli náš referenční úhel (250° – 180° = 70°).