Wahrscheinlichkeit
Lernziel(e)
· Definieren Sie Ereignis, Ergebnis, Versuch, einfaches Ereignis, Beispielraum und berechnen Sie die Wahrscheinlichkeit, dass ein Ereignis auftritt.
· Berechnen Sie die Wahrscheinlichkeit von Ereignissen für komplexere Ergebnisse.
· Lösen Sie Anwendungen mit Wahrscheinlichkeiten.
Einführung
Die Wahrscheinlichkeit gibt an, wie wahrscheinlich es ist, dass etwas passiert., Es ist eine Zahl zwischen und einschließlich der Zahlen 0 und 1. Es kann als Bruch, Dezimalzahl oder Prozent geschrieben werden.

Das zufällige Auswählen von Zahlen bedeutet, dass es keine bestimmte Reihenfolge gibt, in der sie ausgewählt werden. Viele Spiele verwenden Würfel oder Spinner, um zufällig Zahlen zu generieren. Wenn Sie verstehen, wie Wahrscheinlichkeiten berechnet werden, können Sie nachdenkliche Entscheidungen darüber treffen, wie diese Spiele gespielt werden sollen, indem Sie die Wahrscheinlichkeit verschiedener Ergebnisse kennen.,
Definitionen
Zuerst müssen Sie einige Begriffe in Bezug auf Wahrscheinlichkeit kennen. Wenn Sie mit Wahrscheinlichkeit arbeiten, wird eine zufällige Aktion oder Reihe von Aktionen als Versuch bezeichnet. Ein Ergebnis ist das Ergebnis einer Studie, und ein Ereignis ist eine bestimmte Sammlung von Ergebnissen. Ereignisse werden normalerweise unter Verwendung eines gemeinsamen Merkmals der Ergebnisse beschrieben.
Wenden wir diese Sprache an, um zu sehen, wie die Begriffe in der Praxis funktionieren. Einige Spiele erfordern Rollen einen Würfel mit sechs Seiten, nummeriert von 1 zu 6. („Würfel“ ist der plural von Matrize.,) Die folgende Tabelle veranschaulicht die Verwendung von Versuch, Ergebnis und Ereignis für ein solches Spiel:
Beachten Sie, dass eine Sammlung von Ergebnissen in Klammern gesetzt und durch Kommas getrennt wird.
Ein einfaches Ereignis ist ein Ereignis, mit nur einem Ausgang. Das Rollen einer 1 wäre ein einfaches Ereignis, da es nur ein Ergebnis gibt, das funktioniert-1! Das Rollen von mehr als einer 5 wäre auch ein einfaches Ereignis, da das Ereignis nur 6 als gültiges Ergebnis enthält. Ein zusammengesetztes Ereignis ist ein Ereignis mit mehr als einem Ergebnis. Zum Beispiel kann beim Walzen einer sechsseitigen Matrize das Walzen einer geraden Zahl mit einem von drei Ergebnissen auftreten: 2, 4 und 6.,
Wenn Sie einen sechsseitigen Würfel viele Male rollen, sollten Sie nicht erwarten, dass ein Ergebnis häufiger auftritt als ein anderer (vorausgesetzt, es ist ein fairer Würfel). Die Ergebnisse in einer solchen Situation sollen gleichermaßen wahrscheinlich sein. Es ist sehr wichtig zu erkennen, wann Ergebnisse bei der Berechnung der Wahrscheinlichkeit gleich wahrscheinlich sind. Da jedes Ergebnis in der Die-Rolling-Studie gleich wahrscheinlich ist, würden Sie erwarten, dass jedes Ergebnis ![]() der Rollen erhalten wird., Das heißt, Sie würden erwarten, dass
der Rollen erhalten wird., Das heißt, Sie würden erwarten, dass ![]() der Rollen 1,
der Rollen 1, ![]() der Rollen 2,
der Rollen 2, ![]() der Rollen 3 usw. ist.
der Rollen 3 usw. ist.
Ein Spinner ist in vier gleiche Teile unterteilt, die jeweils mit einer anderen Farbe gefärbt sind, wie unten gezeigt. Wenn dieser Spinner gedreht wird, zeigt der Pfeil auf eine der Farben. Sind die Ergebnisse gleich wahrscheinlich?
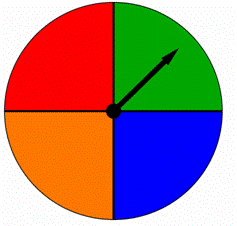
A) ja, Sie sind gleichermaßen wahrscheinlich.
B) Nein, Sie sind nicht gleich wahrscheinlich sind.,
Wahrscheinlichkeit von Ereignissen
Die Wahrscheinlichkeit eines Ereignisses ist, wie oft es erwartet wird, auftreten. Es ist das Verhältnis der Größe des Ereignisraums zur Größe des Probenraums.
Zuerst müssen Sie die Größe des Probenraums bestimmen. Die Größe des Probenraums ist die Gesamtzahl der möglichen Ergebnisse. Wenn Sie beispielsweise 1 Würfel rollen, beträgt der Probenraum 1, 2, 3, 4, 5, oder 6. Die Größe des Probenraums beträgt also 6.
Dann müssen Sie die Größe des Ereignisraums bestimmen., Der Veranstaltungsraum ist die Anzahl der Ergebnisse der Veranstaltung, an der Sie interessiert sind. Der Ereignisraum für das Rollen einer Zahl von weniger als drei ist 1 oder 2. Die Größe des Veranstaltungsraums beträgt also 2.
Für gleich wahrscheinliche Ergebnisse kann die Wahrscheinlichkeit eines Ereignisses E P(E) geschrieben werden.
![]()
|
Beispiel |
||
|
Problem |
Ein Spiel erfordert das Rollen eines sechsseitigen Würfels, der von 1 bis 6 nummeriert ist., Wie hoch ist die Wahrscheinlichkeit, eine gerade Zahl zu rollen? |
|
|
Sample space = {1, 2, 3, 4, 5, 6}
Ereignisraum = {2, 4, 6} |
Suchen Sie zuerst den Beispielraum und den Ereignisraum. Der Probenraum ist alle möglichen Ergebnisse, und der Veranstaltungsraum ist die Ergebnisse in der Veranstaltung. In diesem Fall „rollt“ das Ereignis eine gerade Zahl.,“ |
|
|
|
Da die Ergebnisse gleich wahrscheinlich sind, ist die Wahrscheinlichkeit des Ereignisses das Verhältnis von Ereignisraum zu Probenraum., |
|
|
Answer |
P(gerade Zahl) = |
|
Es ist eine gängige Praxis mit Wahrscheinlichkeiten, wie bei Brüchen im Allgemeinen, eine Wahrscheinlichkeit in niedrigste Begriffe zu vereinfachen, da dies es für die meisten Menschen einfacher macht, ein Gefühl dafür zu bekommen, wie groß es ist. Wenn es keinen Grund gibt, dies nicht zu tun, drücken Sie alle endgültigen Wahrscheinlichkeiten in niedrigsten Begriffen aus.,
Ein Spinner ist in gleiche Teile geteilt, die jeweils mit einer anderen Farbe gefärbt sind, wie unten gezeigt., Finden Sie die Wahrscheinlichkeit, blau oder grün auf diesem Spinner zu drehen:
A) ![]()
B) ![]()
C) 2
D) 6
Zählen Methoden zu finden Probe Räume
Die schwierigste sache für die berechnung einer wahrscheinlichkeit kann die suche nach der größe der probe raum, vor allem, wenn es sind zwei oder mehr studien. Es gibt verschiedene Zählmethoden, die helfen können.,
Der erste, der sich ansieht, ist das Erstellen eines Diagramms. Im folgenden Beispiel dreht Tori zwei Münzen um. Sie müssen also den Probenraum sorgfältig bestimmen. Ein Diagramm wie das im folgenden Beispiel gezeigte ist ein guter Ansatz.
|
Beispiel |
||||
|
Problem |
Tori dreht ein Paar Münzen um und notiert, wie viele „Köpfe“ sie bekommt. Wie hoch ist die Wahrscheinlichkeit, dass sie 2 Köpfe dreht?, Wie hoch ist die Wahrscheinlichkeit, dass sie nur 1 Kopf dreht?,15ecf6″>T |
T |
TT |
|
sample space: {HH, HT, TH, TT}
event space for 2 heads: {HH}
event space for 1 head: {HT, TH}
Create a chart to record the results of flipping the first coin, followed by the result of flipping the second coin.,
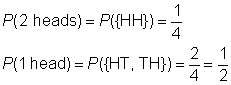
Da die Ergebnisse gleich wahrscheinlich sind, ist die Wahrscheinlichkeit des Ereignisses das Verhältnis von Ereignisraum zu Probenraum.,
Answer
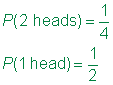
Im folgenden Beispiel ist der Beispielraum für Tori einfach, da nur ein Würfel gerollt wird. Da James jedoch zwei Würfel rollt, hilft ein Diagramm, die Informationen zu organisieren.,
|
Beispiel |
||||||||
|
Problem |
Tori rollte einen sechsseitigen Würfel und wollte ein Ergebnis von 1 oder 4 erhalten. James rollte zwei sechsseitige Würfel, einen blauen und einen roten, und wollte gleichzeitig ein Ergebnis von a 1 und a 3 erzielen. Welches Ereignis hat eine größere Wahrscheinlichkeit?, |
|||||||
|
Tori’s sample space: {1, 2, 3, 4, 5, 6}
Tori’s event space: {1, 4}
Tori:
|
First, find the sample space and the event space for the two trials., Für Toris Prozess ist das unkompliziert. Da die Ergebnisse gleich wahrscheinlich sind, ist die Wahrscheinlichkeit des Ereignisses das Verhältnis von Ereignisraum zu Probenraum.,316594724″> 6 |
6,1 |
6,2 |
6,3 |
6,4 |
6,5 |
6,6 |
|
James‘ sample space has 36 outcomes.,
James‘ Ereignisraum hat 2 Ergebnisse.
Es ist nicht so offensichtlich für James‘ Versuch, da er rollt zwei Würfel. Verwenden Sie ein Diagramm, um die Möglichkeiten zu finden.
Es gibt 36 Ergebnisse. Von diesen gibt es 2, die sowohl 1 als auch 3 haben.,
Id: ![]()
Da die Ergebnisse gleich wahrscheinlich sind, ist die Wahrscheinlichkeit des Ereignisses das Verhältnis von Ereignisraum zu Probenraum.
Antwort
Tori Ereignis hat eine größere Wahrscheinlichkeit.,
Sie können auch ein Baum-Diagramm zu bestimmen, wird die Probe Raum. Ein Baumdiagramm hat einen Zweig für jedes mögliche Ergebnis für jedes Ereignis.
Angenommen, ein Schrank hat drei Paar Hosen (schwarz, weiß und grün), vier Hemden (grün, weiß, lila und gelb) und zwei Paar Schuhe (schwarz und weiß). Wie viele verschiedene Outfits können gemacht werden? Es gibt 3 Möglichkeiten für Hosen, 4 Möglichkeiten für Hemden und 2 Möglichkeiten für Schuhe., Verwenden wir für unser Baumdiagramm B für Schwarz, W für Weiß, G für Grün, P für Lila und Y für Gelb.
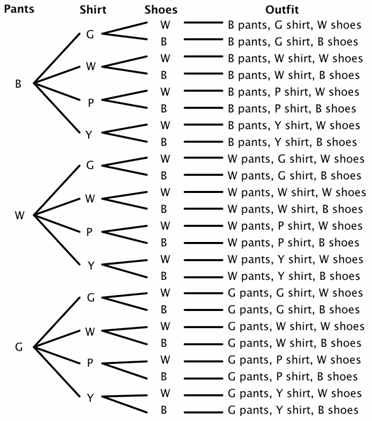
Sie können aus dem Baumdiagramm sehen, dass es 24 mögliche Outfits (einige vielleicht keine gute Wahl) im Beispielraum gibt.
Jetzt könnten Sie ziemlich leicht einige Wahrscheinlichkeitsprobleme lösen. Wie hoch ist beispielsweise die Wahrscheinlichkeit, dass Sie Hosen und Schuhe mit derselben Farbe wählen, wenn Sie die Augen schließen und zufällig auswählen? Sie können sehen, dass es 8 Outfits gibt, in denen die Hose und die Schuhe übereinstimmen.,
![]()
Wie Sie gesehen haben, müssen Sie nicht immer jedes Ergebnis im Probenraum identifizieren, um eine Wahrscheinlichkeit zu berechnen, wenn ein Versuch mehr als ein zufälliges Element umfasst, z. B. mehr als eine Münze umzudrehen oder mehr als einen Würfel zu rollen. Sie benötigen nur die Anzahl der Ergebnisse.
Das grundlegende Zählprinzip ist eine Möglichkeit, die Anzahl der Ergebnisse zu finden, ohne jeden einzelnen aufzulisten und zu zählen.,
Das grundlegende Zählprinzip
Wenn ein Ereignis p mögliche Ergebnisse hat und ein anderes Ereignis m mögliche Ergebnisse hat, dann gibt es insgesamt p • m mögliche Ergebnisse für die beiden Ereignisse.
Beispiele
· Rollen von zwei sechsseitigen Würfeln: Jeder Würfel hat 6 gleich wahrscheinliche Ergebnisse, so dass der Probenraum 6 • 6 oder 36 gleich wahrscheinliche Ergebnisse ist.
· Umdrehen von drei Münzen: Jede Münze hat 2 gleich wahrscheinliche Ergebnisse, so dass der Probenraum ist 2 • 2 • 2 oder 8 ebenso wahrscheinliche Ergebnisse.,
· Rollen eines sechsseitigen Würfels und Umdrehen einer Münze: Der Probenraum ist 6 • 2 oder 12 gleich wahrscheinliche Ergebnisse.
Sie können also das grundlegende Zählprinzip verwenden, um herauszufinden, wie viele Outfits es im vorherigen Beispiel gibt. Es gibt 3 Möglichkeiten für Hosen, 4 Möglichkeiten für Hemden und 2 Möglichkeiten für Schuhe. Mit dem grundlegenden Zählprinzip haben Sie 4 • 3 • 2 = 24 verschiedene Outfits.,
|
Beispiel |
||
|
Problem |
Barry: bei einem Charity-Spaziergang Mittagessen für alle anderen Freiwilligen zu machen. In jede Tüte steckt er: · eines von zwei Sandwiches (Erdnussbutter und Gelee oder Truthahn und Käse), · eines von drei Chips (normale Kartoffelchips, gebackene Kartoffelchips oder Maischips), · ein Stück Obst (ein Apfel oder eine Orange)., Er vergaß zu markieren, was in den Taschen war. Angenommen, jede Wahl ist gleich wahrscheinlich, wie hoch ist die Wahrscheinlichkeit, dass die Tasche, die Therese bekommt, ein Erdnussbutter-Gelee-Sandwich und einen Apfel enthält?, |
|
|
Size of sample space:
(number of sandwich choices) • (number of chip choices) • (number of fruit choices) = 2 • 3 • 2 = 12
|
First, use the Fundamental Counting Principle to find the size of the sample space., |
|
|
Größe des Ereignisraums:
(Anzahl der Ereignisoptionen im Ereignis) • (anzahl der Chipwahlen im Ereignis) • (Anzahl der Fruchtwahlen im Ereignis) = |
Folgen Sie für den Ereignisraum demselben Prinzip. In diesem Fall gibt es nur ein Sandwich und ein Stück Obst von Interesse, aber jede der drei Arten von Chips ist akzeptabel., |
|
|
Answer |
|
Verwenden Sie das Verhältnis, um die Wahrscheinlichkeit zu ermitteln. |
Carrie flips vier Münzen und die Anzahl der Schwänze. Es gibt vier Möglichkeiten, genau einen Schwanz zu bekommen: HHHT, HHTH, HTHH und THHH. Wie hoch ist die Wahrscheinlichkeit, dass Carrie genau einen Schwanz bekommt?,
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Summary
Probability helps you understand random, unpredictable situations where multiple outcomes are possible., Es ist ein Maß für die Wahrscheinlichkeit eines Ereignisses und hängt vom Verhältnis von Ereignis und möglichen Ergebnissen ab, wenn alle diese Ergebnisse gleich wahrscheinlich sind.