Probabilitate
Obiectiv de Învățare(s)
· Definirea evenimentului, rezultatul, proces, eveniment simplu, spațiu probă și se calculează probabilitatea ca un eveniment se va produce.
· calculați probabilitatea evenimentelor pentru rezultate mai complexe.
· rezolva aplicații care implică probabilități.
Introducere
Probabilitate oferă o măsură a cât de probabil este ca ceva se va produce., Este un număr între și inclusiv numerele 0 și 1. Poate fi scris ca o fracție, o zecimală sau un procent.
alege numerele la întâmplare înseamnă că nu există nici o ordine specifică în care sunt alese. Multe jocuri folosesc zaruri sau filaturi pentru a genera numere la întâmplare. Dacă înțelegeți cum să calculați probabilitățile, puteți lua decizii bine gândite despre cum să jucați aceste jocuri, cunoscând probabilitatea unor rezultate diferite.,
Definiții
în Primul rând trebuie să știți unele conditii legate de probabilitate. Când lucrați cu probabilitate, o acțiune aleatorie sau o serie de acțiuni se numește proces. Un rezultat este rezultatul unui proces, iar un eveniment este o colecție specială de rezultate. Evenimentele sunt de obicei descrise folosind o caracteristică comună a rezultatelor.
să aplicăm această limbă pentru a vedea cum funcționează termenii în practică. Unele jocuri necesită rulare o matriță cu șase laturi, numerotate de la 1 la 6. (Dice este pluralul lui die.,) Graficul de mai jos ilustrează utilizarea procesului, a rezultatului și a evenimentului pentru un astfel de joc:
observați că o colecție de rezultate este pusă în bretele și separată prin virgule.un eveniment simplu este un eveniment cu un singur rezultat. Rularea unui 1 ar fi un eveniment simplu, deoarece există un singur rezultat care funcționează-1! Rularea mai mult de 5 ar fi, de asemenea, un eveniment simplu, deoarece evenimentul include doar 6 ca rezultat valid. Un eveniment compus este un eveniment cu mai mult de un rezultat. De exemplu, în rularea unei matrițe cu șase fețe, rularea unui număr par ar putea avea loc cu unul dintre cele trei rezultate: 2, 4 și 6.,când rotiți o matriță cu șase fețe de mai multe ori, nu trebuie să vă așteptați ca niciun rezultat să se întâmple mai des decât altul (presupunând că este o matriță corectă). Se spune că rezultatele într-o situație ca aceasta sunt la fel de probabile. Este foarte important să recunoaștem când rezultatele sunt la fel de probabile atunci când calculăm probabilitatea. Deoarece fiecare rezultat din procesul de rulare este la fel de probabil, v-ați aștepta să obțineți fiecare rezultat 
al rolelor., Asta este, te-ai aștepta de role pentru a fi de 1, de role pentru a fi de 2, de role pentru a fi 3, și așa mai departe.un filator este împărțit în patru părți egale, fiecare colorat cu o culoare diferită, așa cum se arată mai jos. Când acest spinner este rotit, săgeata indică una dintre culori. Sunt rezultatele la fel de probabile?
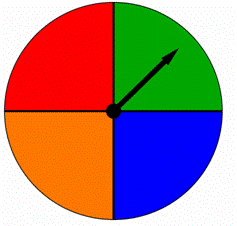
O) Da, sunt la fel de probabile.B) nu, nu sunt la fel de probabile.,
Probabilitatea de Evenimente
probabilitatea unui eveniment este cât de des este de așteptat să apară. Este raportul dintre dimensiunea spațiului de eveniment și dimensiunea spațiului de probă.în primul rând, trebuie să determinați dimensiunea spațiului de probă. Dimensiunea spațiului eșantionului este numărul total de rezultate posibile. De exemplu, atunci când rola 1 muri, spațiul de probă este 1, 2, 3, 4, 5, sau 6. Deci dimensiunea spațiului de probă este de 6.apoi, trebuie să determinați dimensiunea spațiului de evenimente., Spațiul evenimentului este numărul de rezultate în evenimentul care vă interesează. Spațiul de evenimente pentru rularea unui număr mai mic de trei este 1 sau 2. Deci dimensiunea spațiului de evenimente este 2.pentru rezultate la fel de probabile, probabilitatea unui eveniment E poate fi scrisă P(E).
|
Exemplu |
||
|
Problema |
Un joc necesită rulare o moară cu șase laturi numerotate de la 1 la 6., Care este probabilitatea de rulare a unui număr par? |
|
|
Probă de spațiu = {1, 2, 3, 4, 5, 6}
spațiu de Eveniment = {2, 4, 6} |
în Primul rând, găsi eșantion spațiu și spațiu de eveniment. Spațiul de probă este toate rezultatele posibile, iar spațiul evenimentului este rezultatele evenimentului. În acest caz, evenimentul ” rulează un număr par.,” |
|
|
|
Deoarece rezultatele sunt la fel de probabile, probabilitatea unui eveniment este raportul dintre eveniment de spațiu pentru a proba spațiu., |
|
|
Răspunsul |
P(număr par) = |
|
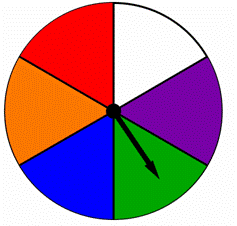
Aceasta este o practică comună cu probabilități, ca și cu fracții, în general, pentru a simplifica o probabilitate în cel mai mic termenii din care face mai ușor pentru cei mai mulți oameni pentru a obține un sentiment de cât de mare este. Dacă nu există motive să nu facă acest lucru, exprima toate probabilitățile finale în termeni mai mici.,un filator este împărțit în părți egale, fiecare colorat cu o culoare diferită, așa cum se arată mai jos., Pentru a găsi probabilitatea de filare albastru sau verde pe acest spinner:
A)
B) 
C) 2
D) 6
Metode de Numărare pentru a găsi Eșantion Spații
Cel mai dificil lucru pentru a calcula o probabilitate poate fi găsirea mărimea eșantionului spațiu, mai ales dacă există două sau mai multe procese. Există mai multe metode de numărare care vă pot ajuta.,
primul care se uită la face o diagramă. În exemplul de mai jos, Tori răstoarnă două monede. Deci, trebuie să determinați cu atenție spațiul de probă. O diagramă precum cea prezentată în exemplul care urmează este o abordare bună.
|
Exemplu |
||||
|
Tori este flipping o pereche de monede și constatând cât de multe flips de „capete”, ea devine. Care este probabilitatea ca ea să răstoarne 2 capete?, Care este probabilitatea ca ea să răstoarne doar 1 cap?,15ecf6″>T |
T |
TT |
||
sample space: {HH, HT, TH, TT}
event space for 2 heads: {HH}
event space for 1 head: {HT, TH}
Create a chart to record the results of flipping the first coin, followed by the result of flipping the second coin.,
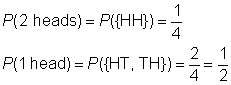
Deoarece rezultatele sunt la fel de probabile, probabilitatea unui eveniment este raportul dintre eveniment de spațiu pentru a proba spațiu.,
Răspunsul
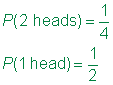
În exemplul de mai jos, spațiul de proba pentru Tori este simplu ca numai unul să moară este de a fi laminate. Cu toate acestea, din moment ce James este de rulare două mor, o diagramă ajută la organizarea informațiilor.,
|
Exemplu |
||||||||
|
Tori laminate o moară cu șase laturi și a vrut pentru a obține un rezultat de 1 sau 4. James a rulat două zaruri cu șase fețe, unul albastru și unul roșu, și a vrut să obțină un rezultat atât de 1, cât și de 3, în același timp. Ce eveniment are o probabilitate mai mare?, |
||||||||
|
Tori’s sample space: {1, 2, 3, 4, 5, 6}
Tori’s event space: {1, 4}
Tori:
|
First, find the sample space and the event space for the two trials., Pentru procesul lui Tori, acest lucru este simplu.deoarece rezultatele sunt la fel de probabile, probabilitatea evenimentului este raportul dintre spațiul evenimentului și spațiul de probă.,316594724″> 6 |
6,1 |
6,2 |
6,3 |
6,4 |
6,5 |
6,6 |
|
James’ sample space has 36 outcomes.,
spațiul de evenimente al lui James are 2 rezultate.
nu este atât de evident pentru procesul lui James, deoarece el rulează două zaruri. Utilizați o diagramă pentru a găsi posibilitățile.
există 36 de rezultate. Dintre acestea, există 2 care au atât 1, cât și 3.,
James: 
Deoarece rezultatele sunt la fel de probabile, probabilitatea unui eveniment este raportul dintre eveniment de spațiu pentru a proba spațiu.
Răspunsul
Tori eveniment are o probabilitate mai mare.,
de asemenea, puteți utiliza o diagramă pentru a determina spațiul de proba. O diagramă arbore are o ramură pentru fiecare rezultat posibil pentru fiecare eveniment.să presupunem că un dulap are trei perechi de pantaloni (negru, alb și verde), patru cămăși (verde, alb, violet și galben) și două perechi de pantofi (alb și negru). Câte echipamente diferite pot fi făcute? Există 3 opțiuni pentru pantaloni, 4 opțiuni pentru cămăși și 2 opțiuni pentru pantofi., Pentru diagrama noastră arbore, să folosim B Pentru negru, W pentru alb, G Pentru verde, P pentru violet și Y pentru galben.
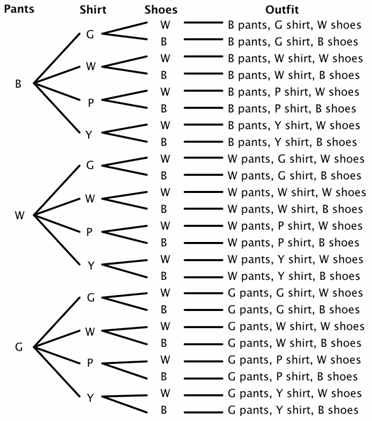
puteți vedea din diagrama arborelui că există 24 de echipamente posibile (unele poate nu alegeri grozave) în spațiul de probă.acum ai putea rezolva destul de ușor unele probleme de probabilitate. De exemplu, care este probabilitatea ca, dacă închideți ochii și alegeți la întâmplare, să alegeți pantaloni și pantofi cu aceeași culoare? Puteți vedea că există 8 ținute în care se potrivesc pantalonii și pantofii.,
după Cum ați văzut, atunci când un proces implică mai mult de un element aleatoriu, cum ar fi flipping mai mult de o monedă sau o rulare mai mult de o moară, nu întotdeauna trebuie să identifice fiecare rezultat în eșantion spațiu pentru a calcula o probabilitate. Ai nevoie doar de numărul de rezultate.principiul fundamental de numărare este o modalitate de a găsi numărul de rezultate fără a le enumera și număra pe fiecare dintre ele.,dacă un eveniment are p rezultate posibile, iar un alt eveniment are M rezultate posibile, atunci există un total de p • m rezultate posibile pentru cele două evenimente.
Exemple
· Rulare doi de șase zaruri fețe: Fiecare zar are 6 rezultate la fel de probabile, astfel încât spațiul de proba este de 6 • 6 sau 36 rezultate la fel de probabile.
* Flipping trei monede: fiecare monedă are 2 rezultate la fel de probabil, astfel încât spațiul de probă este 2 • 2 • 2 sau 8 rezultate la fel de probabile.,
· Rulare o moară cu șase laturi și flipping o monedă: spațiul De proba este de 6 • 2 sau 12 rezultate la fel de probabile.deci, ați putea folosi principiul fundamental de numărare pentru a afla câte echipamente există în exemplul anterior. Există 3 opțiuni pentru pantaloni, 4 opțiuni pentru cămăși și 2 opțiuni pentru pantofi. Folosind principiul fundamental de numărare, aveți 4 • 3 • 2 = 24 utilaje diferite.,
|
Exemplu |
||
|
Barry voluntar la o organizație de caritate de mers pe jos pentru a face pachet pentru toate celelalte voluntari. În fiecare sac își pune: · una din cele două sandwich-uri (cu unt de arahide și jeleu, sau de curcan și brânză), · una din cele trei jetoane (regulat chipsuri de cartofi, chipsuri de cartofi, sau chips-uri de porumb), · o bucată de fruct (un măr sau o portocală).,a uitat să marcheze ce era în saci. Presupunând că fiecare alegere este la fel de probabilă, care este probabilitatea ca punga pe care Therese o primește să dețină un sandwich cu unt de arahide și jeleu și un măr?, |
||
|
Size of sample space:
(number of sandwich choices) • (number of chip choices) • (number of fruit choices) = 2 • 3 • 2 = 12
|
First, use the Fundamental Counting Principle to find the size of the sample space., |
|
|
Dimensiune de spațiu eveniment:
(numărul de alegeri de tip sandwich în eveniment) • (numărul de cip alegeri în eveniment) • (numărul de fructe alegeri în eveniment) = |
Pentru evenimentul spațiu, urmează același principiu. În acest caz, există doar un sandwich și o bucată de fructe de interes, dar oricare dintre cele trei tipuri de chipsuri sunt acceptabile., |
|
|
Răspunsul |
|
Utiliza raportul pentru a găsi probabilitatea. |
Carrie răstoarnă patru monede și numără numărul de cozi. Există patru modalități de a obține exact o coada: HHHT, HHTH, HTHH, și THHH. Care este probabilitatea ca Carrie să primească exact o coadă?,
A) 
B) 
C) 
D) 
Summary
Probability helps you understand random, unpredictable situations where multiple outcomes are possible., Este o măsură a probabilității unui eveniment și depinde de raportul dintre eveniment și rezultatele posibile, dacă toate aceste rezultate sunt la fel de probabile.