Criptare cu Cheie publică

Publicitate

Criptografia cu Cheie Publică

spre Deosebire de criptografie cheie simetrică, nu găsim istorice utilizarea de criptare cu chei publice. Este un concept relativ nou.

criptografia simetrică a fost potrivită pentru organizații precum guvernele, militarii și marile corporații financiare care au fost implicate în comunicarea clasificată.,odată cu răspândirea mai multor rețele de calculatoare nesigure în ultimele decenii, s-a simțit o nevoie reală de a folosi criptografia la scară mai mare. S-a constatat că cheia simetrică nu este practică din cauza provocărilor cu care s-a confruntat pentru gestionarea cheilor. Acest lucru a dat naștere criptosistemelor cu chei publice.

procesul de criptare și decriptare este descris în următoarea ilustrație −

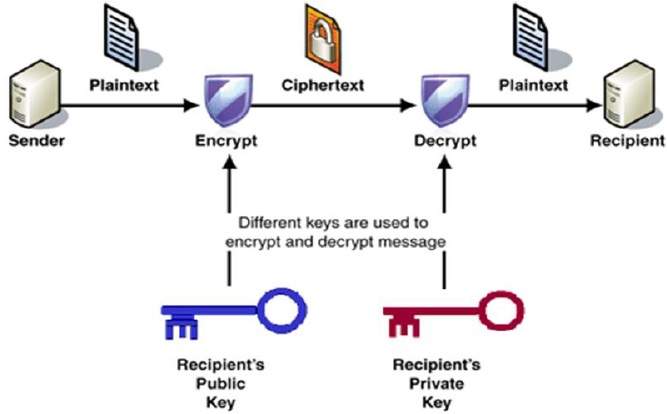
Cele mai importante proprietăți de criptare cu cheie publică sistem sunt −

chei Diferite sunt utilizate pentru criptare și decriptare., Aceasta este o proprietate care stabilește această schemă diferită de schema de criptare simetrică.fiecare receptor are o cheie unică de decriptare, denumită în general cheia sa privată.receptorul trebuie să publice o cheie de criptare, denumită cheia sa publică.o anumită asigurare a autenticității unei chei publice este necesară în această schemă pentru a evita falsificarea de către adversar ca receptor. În general, acest tip de criptosistem implică o terță parte de încredere care certifică faptul că o anumită cheie publică aparține unei anumite persoane sau entități.,
algoritmul de criptare este suficient de complex pentru a interzice atacatorului să deducă textul clar din textul cifrat și cheia de criptare (publică).deși cheile private și publice sunt legate matematic, nu este posibil să se calculeze cheia privată din cheia publică. De fapt, o parte inteligentă a oricărui criptosistem cu cheie publică este în proiectarea unei relații între două chei.există trei tipuri de scheme de criptare a Cheilor Publice., Vom discuta despre ele în următoarele secțiuni –

RSA Cryptosistem

acest cryptosistem este unul sistemul inițial. Rămâne criptosistem cel mai angajat chiar și astăzi. Sistemul a fost inventat de trei savanți Ron Rivest, Adi Shamir și Len Adleman și, prin urmare, este denumit criptosistem RSA.vom vedea două aspecte ale criptosistemului RSA, în primul rând generarea perechii de chei și în al doilea rând algoritmi de criptare-decriptare.,fiecare persoană sau o parte care dorește să participe la comunicare folosind criptarea trebuie să genereze o pereche de chei, și anume cheia publică și cheia privată. Procesul urmat în generarea de chei este descris mai jos −
- pentru a Genera RSA modul (n)
  - Selectați două numere prime mari, p și q.
  - se Calculează n=p*q. Pentru puternic de criptare incasabil, fie n un număr mare, de obicei un minim de 512 biți.,
formează cheia publică
- perechea de numere (n, e) formează cheia publică RSA și este făcută publică.,
- Interesant, deși n este o parte a cheii publice, dificultate în factorizing un mare număr prim asigură că atacatorul nu poate găsi în timp finit a două numere prime (p & q) utilizate pentru a obține n. Aceasta este puterea de RSA.

generați cheia privată

cheia privată d este calculată din P, q și e. pentru N și e dat, există un număr unic d.
Numărul d este inversul e modulo (p – 1)(q – 1)., Aceasta înseamnă că d este numărul mai mic decât (p – 1) (q – 1), astfel încât atunci când este înmulțit cu e, este egal cu 1 modulo(p – 1) (q-1).această relație este scrisă matematic după cum urmează −

ed = 1 mod (p − 1)(q − 1)

algoritmul euclidian extins ia p, q și e ca intrare și dă D ca ieșire.

exemplu

Un exemplu de generare a perechii de chei RSA este prezentat mai jos. (Pentru ușurința înțelegerii, primele p & q luate aici sunt valori mici. Practic, aceste valori sunt foarte mari).,

fie două prime p = 7 și q = 13. Astfel, modulul n = pq = 7 x 13 = 91.
selectați e = 5, care este o alegere validă, deoarece nu există nici un număr care este factorul comun de 5 și(P − 1) (q− 1) = 6 × 12 = 72, cu excepția 1.perechea de numere (n, e) = (91, 5) formează cheia publică și poate fi pusă la dispoziția oricui dorește să ne poată trimite mesaje criptate.
intrare p = 7, q = 13 și e = 5 la algoritmul euclidian extins. Rezultatul va fi d = 29.,
Verificați că d calculat este corect de calcul −

de = 29 × 5 = 145 = 1 mod 72

prin Urmare, cheia publică este (91, 5) și chei private este (91, 29).odată ce perechea de chei a fost generată, procesul de criptare și decriptare este relativ simplu și ușor din punct de vedere computațional.interesant este că RSA nu funcționează direct pe șiruri de biți ca în cazul criptării simetrice a cheilor. Funcționează pe numere modulo n. Prin urmare, este necesar să reprezentăm textul clar ca o serie de numere mai mici decât n.,să presupunem că expeditorul dorește să trimită un mesaj text unei persoane a cărei cheie publică este (n, E).
expeditor atunci reprezintă plaintext ca o serie de numere mai mici decât n.
Pentru a cripta primul text clar P, care este un număr modulo n. Procesul de criptare este matematice simple pas −

C = Pe mod n

cu alte cuvinte, textul cifrat C este egală cu text clar P înmulțit cu el însuși e ori și apoi redus modulo n. Acest lucru înseamnă că C este, de asemenea, un număr mai mic decât n.,revenind la exemplul nostru de generare a cheilor cu plaintext P = 10, obținem ciphertext C −

C = 105 mod 91

RSA decriptare

procesul de decriptare pentru RSA este, de asemenea, foarte simplu. Să presupunem că receptorul perechii de chei publice (n, E) a primit un text cifrat C.
receptorul ridică C la puterea cheii sale private d. rezultatul modulo n va fi textul P.,

Plaintext = Cd mod n

se Întoarce din nou la noi, un exemplu numeric, textul cifrat C = 82-ar decriptate la numărul 10, folosind cheia privată a 29 −

Plaintext = 8229 mod 91 = 10

RSA Analiza

securitatea RSA depinde de punctele forte de două funcții separate. Criptosistemul RSA este cel mai popular puterea criptosistemului cu cheie publică, care se bazează pe dificultatea practică de a factoriza numerele foarte mari.,

Funcția de Criptare − este considerată ca un mod de funcția de conversie text clar în text cifrat și poate fi anulată numai cu cunoștințe de cheia privată d.

Generare Cheie − dificultatea de a stabili o cheie privată de un RSA cu cheie publică este echivalent cu factoring modulul n. Un atacator, astfel, nu poate folosi cunoștințele unui RSA cu cheie publică pentru a stabili o cheie privată RSA dacă nu pot factor n. Este, de asemenea, o funcție, la p & q valori pentru modulul n este ușor, dar invers nu este posibil.,dacă oricare dintre aceste două funcții sunt dovedite non-unidirecționale, atunci RSA va fi rupt. De fapt, dacă se dezvoltă eficient o tehnică de factoring, atunci RSA nu va mai fi în siguranță.puterea criptării RSA scade drastic împotriva atacurilor dacă numărul p și q nu sunt prime mari și/ sau cheia publică aleasă e este un număr mic.

Elgamal Cryptosistem

împreună cu RSA, există alte criptosisteme cu cheie publică propuse. Multe dintre ele se bazează pe diferite versiuni ale problemei logaritmului discret.,

criptosistemul ElGamal, numit varianta curbei eliptice, se bazează pe problema logaritmului discret. Ea derivă puterea de la presupunerea că logaritmii discrete nu pot fi găsite în intervalul de timp practic pentru un anumit număr, în timp ce funcționarea inversă a puterii poate fi calculată eficient.să trecem printr-o versiune simplă a ElGamal care funcționează cu numere modulo p. În cazul variantelor de curbe eliptice, se bazează pe sisteme de numere destul de diferite.,

Generație de ElGamal Pereche de chei

Fiecare utilizator de ElGamal criptosistem generează perechea de chei prin după cum urmează −

Alegerea unei prime mari p. În general, un prim număr de 1024 2048 biți lungime este ales.
alegerea unui element generator g.
- Acest număr trebuie să fie între 1 și p-1, dar nu poate fi niciun număr.este un generator al grupului multiplicativ de numere întregi modulo p. aceasta înseamnă că pentru fiecare număr întreg M co-Prim la p, există un număr întreg k astfel încât gk=a mod n.,
  
  de exemplu, 3 este generator de grup 5 (Z5 = {1, 2, 3, 4}).

N	3n	3n mod 5
1	3	3
2	9	4
3	27	2
4	81	1

Alegerea cheii private. Cheia privată x este orice număr mai mare decât 1 și mai mic decât p−1.
partea de calcul a cheii publice., Valoarea y este calculată din parametrii p, g și cheia privată x după cum urmează −

y = gx mod p

obținerea cheii publice. Cheia publică ElGamal constă din cei trei parametri (p, g, y).de exemplu, să presupunem că p = 17 și că g = 6 (se poate confirma că 6 este un generator al grupului Z17). Cheia privată x poate fi orice număr mai mare decât 1 și mai mic decât 71, deci alegem x = 5. Valoarea y este apoi calculată după cum urmează −

y = 65 mod 17 = 7

astfel, cheia privată este 62 și cheia publică este (17, 6, 7).,

criptare și decriptare

generarea unei perechi de chei ElGamal este relativ mai simplă decât procesul echivalent pentru RSA. Dar criptarea și decriptarea sunt puțin mai complexe decât RSA.

Criptare ElGamal

să Presupunem că expeditorul dorește să trimită un text clar pentru cineva al cărui ElGamal cu cheie publică este (p, g, y), atunci −

Expeditor reprezintă plaintext ca o serie de numere modulo p.
Pentru a cripta primul text clar P, care este reprezentat ca un număr modulo p., Procesul de criptare pentru a obține textul cifrat C este după cum urmează −
- genera Aleatoriu un număr k;
- Calcula două valori C1 și C2, unde −

C1 = gk mod pC2 = (P*yk) mod p

Trimite textul cifrat C, constând din două valori (C1, C2), trimis împreună.,
Referindu-se la noastre ElGamal cheie generație exemplul dat mai sus, plaintext P = 13 este codificată după cum urmează −
- genera Aleatoriu un număr k = 10
- Calcula două valori C1 și C2, unde −

C1 = 610 mod 17C2 = (13*710) mod 17 = 9

Trimite textul cifrat C = (C1, C2) = (15, 9).,pentru a decripta textul cifrat (C1, C2) folosind cheia privată x, sunt făcuți următorii doi pași −
- calculați inversul modular al lui (C1)x modulo p, care este (C1)-x , denumit în general factor de decriptare.,
- Obține plaintext folosind următoarea formulă −

C2 × (C1)-x mod p = Plaintext

În exemplul nostru, pentru a decripta textul cifrat C = (C1, C2) = (15, 9), folosind cheia privată a x = 5, decriptarea factor este

15-5 mod 17 = 9

Extractul de text clar P = (9 × 9) mod 17 = 13.

ElGamal Analiza

În ElGamal sistem, fiecare utilizator are o cheie privată x. și are trei componente cheie publică − prim modul p, generator g, publice și Y = g mod p., Puterea Elgamalului se bazează pe dificultatea problemei logaritmului discret.

Dimensiunea cheii securizate este în general > 1024 biți. Astăzi sunt folosite chiar și 2048 biți cheie lungă. Pe frontul vitezei de procesare, Elgamal este destul de lent, este utilizat în principal pentru protocoalele de autentificare cheie. Datorită eficienței mai mari a procesării, variantele eliptice ale curbei ElGamal devin din ce în ce mai populare.,criptografia curbei eliptice (ecc)

criptografia curbei eliptice (ECC) este un termen folosit pentru a descrie o suită de instrumente și protocoale criptografice a căror securitate se bazează pe versiuni speciale ale problemei logaritmului discret. ECC se bazează pe seturi de numere care sunt asociate cu obiecte matematice numite curbe eliptice. Există reguli pentru adăugarea și calcularea multiplilor acestor numere, la fel cum există și pentru numerele modulo p.,ecc include o variantă a multor scheme criptografice care au fost inițial proiectate pentru numere modulare, cum ar fi criptarea ElGamal și algoritmul de semnătură digitală.se crede că problema logaritmului discret este mult mai dificilă atunci când este aplicată punctelor de pe o curbă eliptică. Acest lucru solicită trecerea de la numere modulo p la puncte pe o curbă eliptică. De asemenea, un nivel de securitate echivalent poate fi obținut cu chei mai scurte dacă folosim variante bazate pe curbe eliptice.,tastele mai scurte au ca rezultat două beneficii –

ușurința de gestionare a cheilor
calcul eficient

aceste beneficii fac variantele bazate pe curba eliptică ale schemei de criptare extrem de atractive pentru aplicații în care resursele de calcul sunt constrânse.

schemele RSA și ElGamal – o comparație

să comparăm pe scurt schemele RSA și ElGamal pe diferite aspecte.

RSA	ElGamal
este mai eficient pentru criptare.	este mai eficient pentru decriptare.,
este mai puțin eficient pentru decriptare.	este mai eficient pentru decriptare.pentru un anumit nivel de securitate, sunt necesare chei lungi în RSA.	pentru același nivel de securitate, sunt necesare chei foarte scurte.
este larg acceptat și utilizat.	este nou și nu foarte popular în piață.

Publicitate

Avenir

Condominium