pentru a utiliza calculatorul unghiului de referință, introduceți pur și simplu orice unghi în caseta de unghi pentru a găsi unghiul său de referință, care este unghiul acut care corespunde unghiului introdus. Calculatorul aplică automat Regulile pe care le vom examina mai jos.
ce este un unghi de referință, oricum?
Imaginați-vă un plan de coordonate. Să presupunem că vrem să desenăm un unghi de 144° în avionul nostru., Începem din partea dreaptă a axei x, unde ora trei este pe un ceas. Rotim în sens invers acelor de ceasornic, care începe prin deplasarea în sus. Continuăm să trecem de punctul de 90° (partea superioară a axei y) până ajungem la 144°. Tragem o rază de la origine, care este centrul planului, până la acel punct. Acum avem o rază pe care o numim partea terminală. Dar trebuie să tragem încă o rază pentru a face un unghi. Avem de ales în acest moment. A doua rază trebuie să fie pe axa X. Dacă o tragem de la origine spre partea dreaptă, vom fi tras un unghi care măsoară 144°., Dacă o tragem spre stânga, vom fi tras un unghi care măsoară 36°. Acest al doilea unghi este unghiul de referință. Este întotdeauna cel mai mic dintre cele două unghiuri, va fi întotdeauna mai mic sau egal cu 90° și va fi întotdeauna pozitiv. Iată o animație care arată un unghi de referință pentru patru unghiuri diferite, fiecare dintre acestea fiind într-un cadran diferit. Observați cum a doua rază este întotdeauna pe axa X.
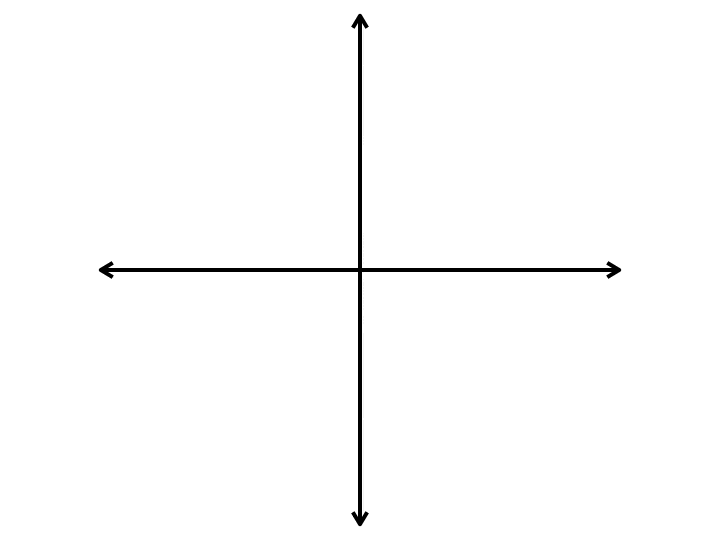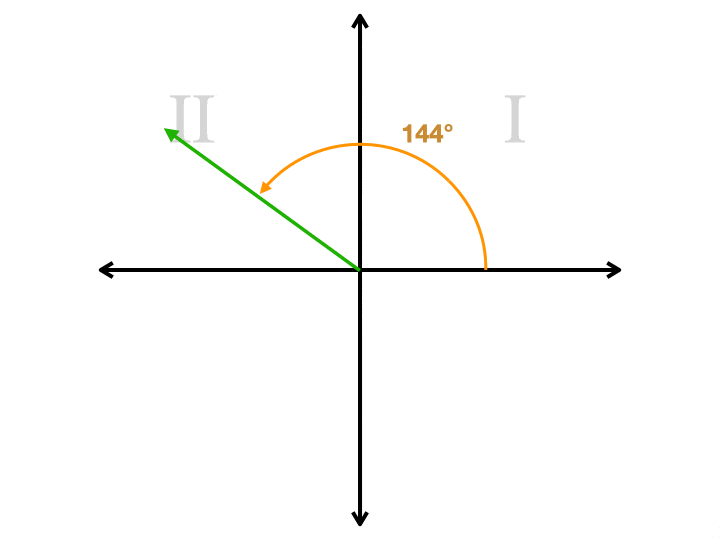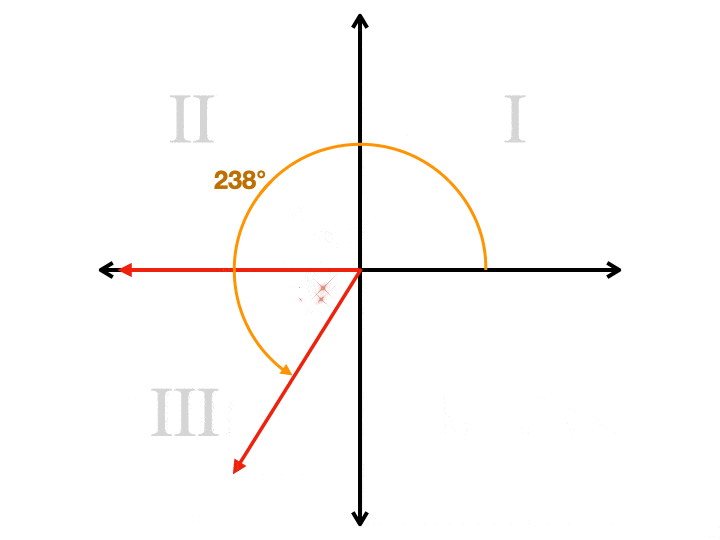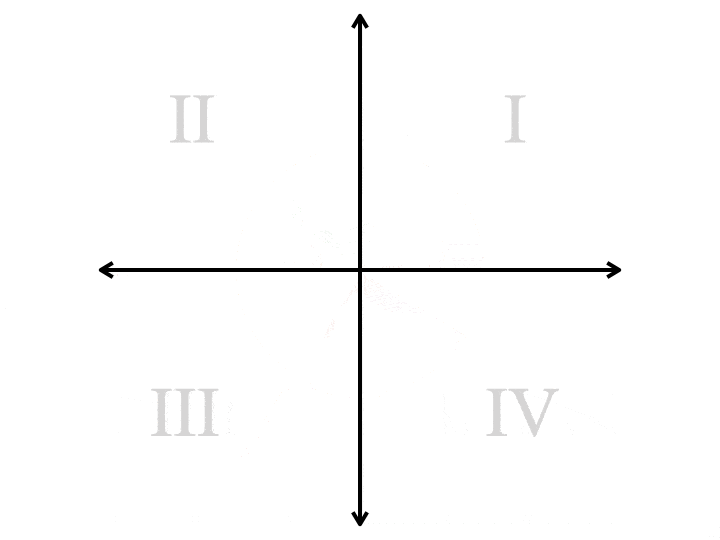
cum este util unghiul de referință?
unghiul de referință are întotdeauna aceleași valori ale funcției trigonometrice ca și unghiul inițial. Observați cuvântul valori acolo., Semnul poate să nu fie același, dar valoarea va fi întotdeauna. Acest lucru este util pentru unghiuri comune precum 45° și 60° pe care le vom întâlni din nou și din nou. Odată ce le cunoaștem valorile sinusoidale, cosinus și tangente, cunoaștem și valorile pentru orice unghi al cărui unghi de referință este de asemenea 45° sau 60°. În ceea ce privește semnul, amintiți-vă că sinusul este pozitiv în cadranul 1 și 2, iar cosinusul este pozitiv în cadranul 1 și 4.
cum găsim unghiul de referință fără un Calculator?
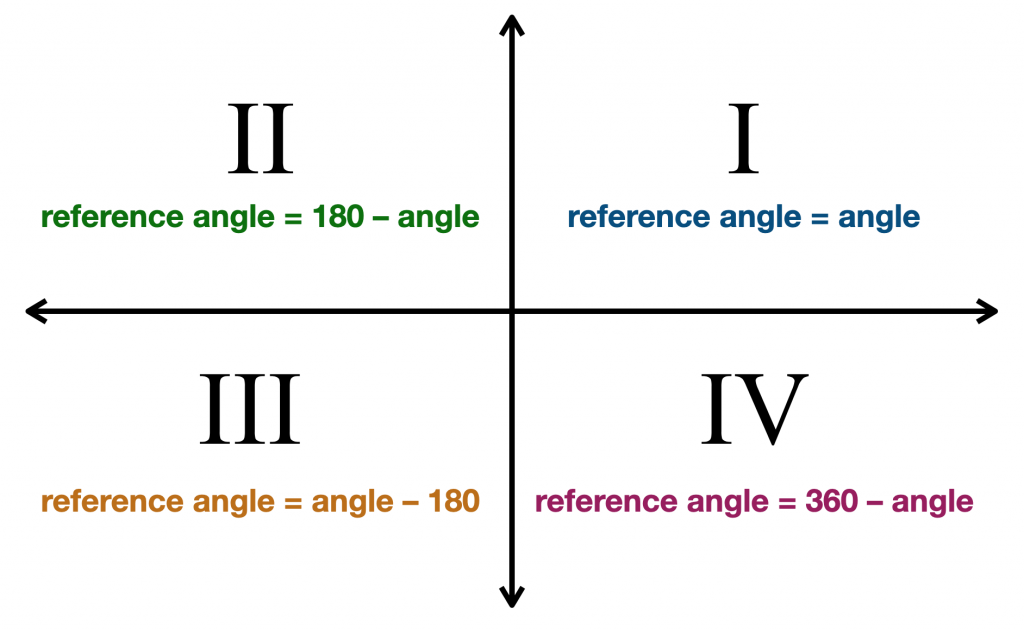
Cum găsim unghiul de referință depinde de cadranul laturii terminale., când partea terminală se află în primul cadran (unghiuri de la 0° la 90°), unghiul nostru de referință este același cu unghiul nostru dat. Acest lucru are sens, deoarece toate unghiurile din primul cadran sunt mai mici de 90°. Deci, dacă unghiul nostru dat este de 33°, atunci unghiul său de referință este de asemenea de 33°. când partea terminală se află în al doilea cadran (unghiuri de la 90° la 180°), unghiul nostru de referință este de 180° minus unghiul nostru dat. Deci, dacă unghiul nostru dat este de 110°, atunci unghiul său de referință este de 180° – 110° = 70°., când partea terminală se află în al treilea cadran (unghiuri de la 180° la 270°), unghiul nostru de referință este unghiul nostru dat minus 180°. Deci, dacă unghiul nostru dat este de 214°, atunci unghiul său de referință este de 214° – 180° = 34°. când partea terminală se află în al patrulea cadran (unghiuri de la 270° la 360°), unghiul nostru de referință este de 360° minus unghiul nostru dat. Deci, dacă unghiul nostru dat este de 332°, atunci unghiul său de referință este de 360° – 332° = 28°.
ce se întâmplă dacă unghiul nostru este mai mare de 360°?,
când un unghi este mai mare de 360°, înseamnă că s-a rotit în jurul planului de coordonate și a continuat să meargă. Pentru a găsi unghiul de referință, trebuie mai întâi să găsim unghiul corespunzător între 0° și 360°. Acest lucru este ușor de făcut. Continuăm să scădem 360 din ea până când este sub 360. De exemplu, dacă unghiul nostru este de 544°, am scădea 360° din acesta pentru a obține 184° (544° – 360° = 184°). Acum am observa că este în al treilea cuadrant, așa că am scădea 180° din el pentru a afla că unghiul nostru de referință este 4°.
ce se întâmplă dacă unghiul nostru este negativ?,
când un unghi este negativ, mutăm cealaltă direcție pentru a găsi partea noastră terminală. Aceasta înseamnă că ne mișcăm în sensul acelor de ceasornic în loc de invers acelor de ceasornic atunci când îl desenăm. Sau îl putem calcula pur și simplu adăugându-l la 360°. De exemplu, dacă unghiul nostru dat este -110°, atunci l-am adăuga la 360° pentru a găsi unghiul nostru pozitiv de 250° (-110° + 360° = 250°). Acum ar trebui să vedem că suntem în al treilea cadran și să aplicăm această regulă pentru a găsi unghiul nostru de referință (250° – 180° = 70°).