Public Key Cryptography
Im Gegensatz zur symmetrischen Schlüsselkryptographie finden wir keine historische Verwendung der Public-Key-Kryptographie. Es ist ein relativ neues Konzept.
Die symmetrische Kryptographie war gut geeignet für Organisationen wie Regierungen, Militärs und große Finanzunternehmen, die an der klassifizierten Kommunikation beteiligt waren.,
Mit der Verbreitung unsichererer Computernetzwerke in den letzten Jahrzehnten wurde ein echtes Bedürfnis verspürt, Kryptographie in größerem Maßstab einzusetzen. Der symmetrische Schlüssel gefunden wurde, nicht praktische aufgrund von Herausforderungen konfrontiert, für das Schlüssel-management. Dies führte zu den Kryptosystemen mit öffentlichem Schlüssel.
Der Prozess der Verschlüsselung und Entschlüsselung ist in der folgenden Abbildung dargestellt –
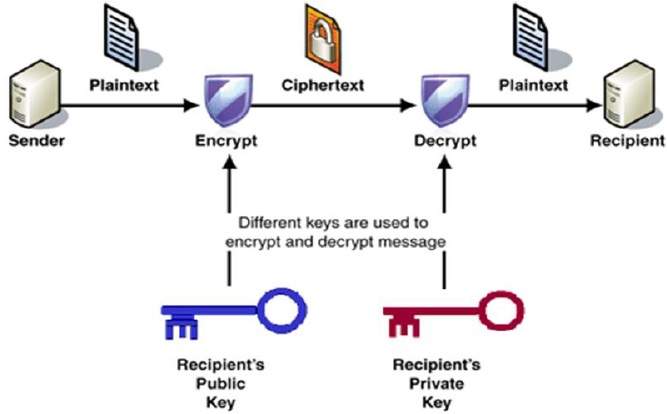
Die wichtigsten Eigenschaften von Public key encryption scheme sind –
-
Verschiedene Schlüssel werden für die Verschlüsselung und Entschlüsselung verwendet., Dies ist eine Eigenschaft, die festgelegt, diese Regelung anders als die symmetrische Verschlüsselung.
-
Jeder Empfänger besitzt einen eindeutigen Entschlüsselungsschlüssel, der allgemein als sein privater Schlüssel bezeichnet wird.
-
Der Empfänger muss einen Verschlüsselungsschlüssel veröffentlichen, der als öffentlicher Schlüssel bezeichnet wird.
-
In diesem Schema ist eine gewisse Sicherheit der Authentizität eines öffentlichen Schlüssels erforderlich, um ein Spoofing durch den Gegner als Empfänger zu vermeiden. Im Allgemeinen handelt es sich bei dieser Art von Kryptosystem um vertrauenswürdige Dritte, die bescheinigen, dass ein bestimmter öffentlicher Schlüssel nur einer bestimmten Person oder Entität gehört.,
-
Verschlüsselungsalgorithmus ist komplex genug, um Angreifer zu verbieten, den Klartext aus dem Chiffretext und die Verschlüsselung abzuleiten (öffentlich) Schlüssel.
-
Obwohl private und öffentliche Schlüssel mathematisch verwandt sind, ist es nicht möglich, den privaten Schlüssel aus dem öffentlichen Schlüssel zu berechnen. In der Tat besteht der intelligente Teil eines Kryptosystems mit öffentlichem Schlüssel darin, eine Beziehung zwischen zwei Schlüsseln zu entwerfen.
Es gibt drei Arten von Verschlüsselungsschemata für öffentliche Schlüssel., Wir diskutieren sie in folgenden Abschnitten –
RSA Cryptosystem
Dieses Cryptosystem ist eines der ersten System. Es bleibt die meisten beschäftigt Kryptosystem auch heute noch. Das System wurde von drei Gelehrten Ron Rivest, Adi Shamir und Len Adleman erfunden und wird daher als RSA Cryptosystem bezeichnet.
Wir werden zwei Aspekte des RSA-Kryptosystems sehen, erstens die Generierung von Schlüsselpaaren und zweitens Verschlüsselungs-Entschlüsselungsalgorithmen.,
Generierung von RSA-Schlüsselpaaren
Jede Person oder Partei, die an der Kommunikation über Verschlüsselung teilnehmen möchte, muss ein Schlüsselpaar generieren, nämlich den öffentlichen Schlüssel und den privaten Schlüssel. Der bei der Schlüsselgenerierung folgende Vorgang wird nachfolgend beschrieben:
-
Erzeugen Sie den RSA-Modul (n)
-
Wählen Sie zwei große Primzahlen aus, p und q.
-
Berechnen Sie n=p*q. Für eine starke unzerbrechliche Verschlüsselung sei n eine große Zahl, typischerweise mindestens 512 Bit.,
-
-
Finden Abgeleitete Anzahl (e)
-
Anzahl e muss größer als 1 und weniger als(p − 1) (q − 1).
-
Es darf keinen gemeinsamen Faktor für e und (p − 1)(q − 1) außer 1 geben. Mit anderen Worten sind zwei Zahlen e und(p – 1) (q – 1) koprime.
-
-
Bilden Sie den öffentlichen Schlüssel
-
Das Zahlenpaar (n, e) bildet den öffentlichen RSA-Schlüssel und wird veröffentlicht.,
-
Obwohl n Teil des öffentlichen Schlüssels ist, stellt die Schwierigkeit, eine große Primzahl zu faktorisieren, interessanterweise sicher, dass der Angreifer die beiden Primzahlen (p& q), die zum Erhalten von n verwendet werden, nicht in endlicher Zeit finden kann.
-
-
Generieren Sie den privaten Schlüssel
-
Der private Schlüssel d wird aus p, q und e berechnet. Für gegebene n und e gibt es eine eindeutige Zahl d.
-
Die Zahl d ist die Umkehrung von e modulo(p – 1) (q – 1)., Dies bedeutet, dass d die Zahl kleiner als (p – 1)(q – 1) ist, so dass sie, wenn sie mit e multipliziert wird, gleich 1 Modulo (p – 1)(q – 1) ist.
-
Diese Beziehung wird mathematisch wie folgt geschrieben –
-
ed = 1 mod (p − 1)(q − 1)
Der erweiterte euklidische Algorithmus nimmt p, q und e als Eingabe und gibt d als Ausgabe an.
Beispiel
Ein Beispiel für die Erzeugung von RSA-Schlüsselpaaren ist unten angegeben. (Zum leichteren Verständnis sind die hier genommenen Primzahlen p & q kleine Werte. Praktisch sind diese Werte sehr hoch).,
-
Zwei Primzahlen seien p = 7 und q = 13. Somit ist der Modul n = pq = 7 x 13 = 91.
-
Wählen Sie e = 5, was eine gültige Wahl ist, da es keine Zahl gibt, die ein gemeinsamer Faktor von 5 und(p − 1) (q) ist− 1) = 6 × 12 = 72, außer 1.
-
Das Zahlenpaar (n, e) = (91, 5) bildet den öffentlichen Schlüssel und kann jedem zur Verfügung gestellt werden, dem wir verschlüsselte Nachrichten senden möchten.
-
Eingabe p = 7, q = 13 und e = 5 an den erweiterten euklidischen Algorithmus. Die Ausgabe ist d = 29.,
-
Überprüfen Sie, ob das berechnete d korrekt ist, indem Sie –
de = 29 × 5 = 145 = 1 mod 72
-
de = 29 × 5 = 145 = 1 mod 72
-
Daher ist der öffentliche Schlüssel (91, 5) und der private Schlüssel (91, 29).
Verschlüsselung und Entschlüsselung
Sobald das Schlüsselpaar generiert wurde, ist der Prozess der Verschlüsselung und Entschlüsselung relativ einfach und rechnerisch einfach.
Interessanterweise arbeitet RSA nicht direkt mit Bitfolgen wie bei der symmetrischen Schlüsselverschlüsselung. Es arbeitet mit Zahlen modulo n. Daher ist es notwendig, den Klartext als eine Reihe von Zahlen darzustellen, die kleiner als n sind.,
RSA-Verschlüsselung
-
Angenommen, der Absender möchte eine Textnachricht an jemanden senden, dessen öffentlicher Schlüssel (n, e) ist.
-
Der Absender repräsentiert dann den Klartext als eine Reihe von Zahlen kleiner als n.
-
Um den ersten Klartext P zu verschlüsseln, der eine Zahl modulo n. Der Verschlüsselungsprozess ist einfach mathematischer Schritt as −
C = Pe mod n
-
Mit anderen Worten, der Chiffretext C ist gleich dem klartext P multipliziert mit sich selbst e-mal und reduziert dann Modulo n. Dies bedeutet, dass C auch eine Zahl kleiner als n ist. ,
-
Zurück zu unserem Beispiel für die Schlüsselgenerierung mit Klartext P = 10 erhalten wir den Chiffretext C –
C = 105 mod 91
RSA-Entschlüsselung
-
Der Entschlüsselungsprozess für RSA ist ebenfalls sehr einfach. Angenommen, der Empfänger des Public-Key-Paares (n, e) hat einen Chiffretext C erhalten.
-
Empfänger erhöht C auf die Leistung seines privaten Schlüssels d. Das Ergebnis modulo n ist der Klartext P.,
Plaintext = Cd mod n
-
Zurück zu unserem numerischen Beispiel würde der Chiffretext C = 82 mit dem privaten Schlüssel 29 auf Nummer 10 entschlüsselt werden −
Plaintext = 8229 mod 91 = 10
RSA-Analyse
Die Sicherheit von RSA hängt von den Stärken zweier separater Funktionen ab. Das RSA-Kryptosystem ist das beliebteste Public-Key-Kryptosystem, dessen Stärke auf der praktischen Schwierigkeit beruht, die sehr großen Zahlen zu berücksichtigen.,
-
Verschlüsselungsfunktion − Sie wird als Einwegfunktion zur Umwandlung von Klartext in Chiffretext angesehen und kann nur mit Kenntnis des privaten Schlüssels rückgängig gemacht werden d.
-
Schlüsselgenerierung-Die Schwierigkeit, einen privaten Schlüssel aus einem öffentlichen RSA − Schlüssel zu bestimmen, entspricht der Faktorierung des Moduls n. Ein Angreifer kann daher die Kenntnis eines öffentlichen RSA-Schlüssels nicht verwenden, um einen privaten RSA-Schlüssel zu bestimmen, es sei denn, er kann n faktorisieren. & q values to modul n is easy but reverse is not possible. ,
Wenn sich herausstellt, dass eine dieser beiden Funktionen nicht einweg ist, wird RSA unterbrochen. Wenn eine Technik zum effizienten Factoring entwickelt wird, ist RSA nicht mehr sicher.
Die Stärke der RSA-Verschlüsselung sinkt drastisch gegen Angriffe, wenn die Zahl p und q keine großen Primzahlen sind und / oder der öffentliche Schlüssel e eine kleine Zahl ist.
ElGamal Kryptosystem
Zusammen mit RSA, gibt es andere public-key cryptosystems vorgeschlagen. Viele von ihnen basieren auf verschiedenen Versionen des diskreten Logarithmus-Problems.,
Das ElGamal-Kryptosystem, elliptische Kurvenvariante genannt, basiert auf dem diskreten Logarithmus-Problem. Es leitet die Stärke aus der Annahme ab, dass die diskreten Logarithmen in einem Zeitrahmen für eine bestimmte Zahl nicht gefunden werden können, während der umgekehrte Betrieb der Leistung effizient berechnet werden kann.
Lassen Sie uns eine einfache Version von ElGamal durchgehen, die mit Zahlen modulo p. Bei elliptischen Kurvenvarianten basiert sie auf ganz unterschiedlichen Zahlensystemen.,
Generierung von ElGamal-Schlüsselpaaren
Jeder Benutzer von ElGamal cryptosystem generiert das Schlüsselpaar wie folgt –
-
Auswahl einer großen Primzahl p. Im Allgemeinen wird eine Primzahl von 1024 bis 2048 Bit Länge gewählt.
-
Auswahl eines Generatorelements g.
-
Diese Zahl muss zwischen 1 und p − 1 liegen, darf aber keine Zahl sein.
-
Es ist ein Generator der multiplikativen Gruppe von Ganzzahlen modulo p. Dies bedeutet,dass für jede Ganzzahl m co-Primzahl bis p eine Ganzzahl k so ist, dass gk=a mod n.,
Zum Beispiel ist 3 Generator der Gruppe 5 (Z5 = {1, 2, 3, 4}).
-
N 3n 3n mod 5 1 3 3 2 9 4 3 27 2 4 81 1 -
Auswahl des privaten Schlüssels. Der private Schlüssel x ist eine beliebige Zahl größer als 1 und kleiner als p−1.
-
Berechnen eines Teils des öffentlichen Schlüssels., Der Wert y wird aus den Parametern p, g und dem privaten Schlüssel x wie folgt berechnet –
y = gx mod p
-
Abrufen des öffentlichen Schlüssels. Der öffentliche ElGamal-Schlüssel besteht aus den drei Parametern (p, g, y).
Angenommen, p = 17 und g = 6 (Es kann bestätigt werden, dass 6 ein Generator der Gruppe Z17 ist). Der private Schlüssel x kann eine beliebige Zahl größer als 1 und kleiner als 71 sein, also wählen wir x = 5. Der Wert y wird dann wie folgt berechnet –
y = 65 mod 17 = 7
-
Somit ist der private Schlüssel 62 und der öffentliche Schlüssel ist (17, 6, 7).,
Verschlüsselung und Entschlüsselung
Die Erzeugung eines ElGamal-Schlüsselpaares ist vergleichsweise einfacher als der entsprechende Prozess für RSA. Aber die Verschlüsselung und Entschlüsselung sind etwas komplexer als RSA.
ElGamal-Verschlüsselung
Angenommen, der Absender möchte einen Klartext an jemanden senden, dessen öffentlicher ElGamal-Schlüssel (p, g, y) ist, dann −
-
Der Absender repräsentiert den Klartext als eine Reihe von Zahlen modulo p.
-
Um den ersten Klartext P zu verschlüsseln, der als Zahl modulo p dargestellt wird., Der Verschlüsselungsprozess, um den Chiffretext C zu erhalten, ist wie folgt –
- Erzeugt zufällig eine Zahl k;
- Berechnen Sie zwei Werte C1 und C2, wobei −
C1 = gk mod pC2 = (P*yk) mod p
-
Senden Sie den Chiffretext C, bestehend aus den beiden getrennten Werten (C1, C2), die zusammen gesendet werden.,
-
In Bezug auf unser ElGamal −Schlüsselgenerierungsbeispiel oben wird der Klartext P = 13 wie folgt verschlüsselt −
- Generieren Sie zufällig eine Zahl, z. B. k = 10
- Berechnen Sie die beiden Werte C1 und C2, wobei –
-
C1 = 610 mod 17C2 = (13*710) mod 17 = 9
-
Senden Sie den Chiffretext C = (C1, C2) = (15, 9).,
ElGamal-Entschlüsselung
-
Um den Chiffretext (C1, C2) mit dem privaten Schlüssel x zu entschlüsseln, werden die folgenden zwei Schritte ausgeführt −
-
Berechnen Sie die modulare Umkehrung von (C1)x modulo p, das (C1)-x ist , im Allgemeinen als Entschlüsselungsfaktor bezeichnet.,
-
Erhalten Sie den Klartext mit der folgenden Formel −
-
C2 × (C1)-x mod p = Plaintext
-
Um den Chiffretext C = (C1, C2) = (15, 9) mit dem privaten Schlüssel x = 5 zu entschlüsseln, ist der Entschlüsselungsfaktor
15-5 mod 17 = 9
-
Klartext extrahieren P = (9 × 9) mod 17 = 13.
ElGamal-Analyse
Im ElGamal-System hat jeder Benutzer einen privaten Schlüssel x. und hat drei Komponenten des öffentlichen Schlüssels-Prime-Modul p, Generator g und public Y = gx mod p., Die Stärke des ElGamal basiert auf der Schwierigkeit des logarithmischen Problems.
Die sichere Schlüsselgröße ist im Allgemeinen > 1024 Bits. Heute werden sogar 2048 Bit lange Schlüssel verwendet. Im Hinblick auf die Verarbeitungsgeschwindigkeit ist Elgamal ziemlich langsam und wird hauptsächlich für Schlüsselauthentifizierungsprotokolle verwendet. Aufgrund der höheren Verarbeitungseffizienz werden elliptische Kurvenvarianten von ElGamal immer beliebter.,
Elliptic Curve Cryptography (ECC)
Elliptic Curve Cryptography (ECC) ist ein Begriff, der verwendet wird, um eine Reihe von kryptografischen Tools und Protokollen zu beschreiben, deren Sicherheit auf speziellen Versionen des diskreten Logarithmus basiert Problem. Es werden keine Zahlen modulo p verwendet.
ECC basiert auf Zahlensätzen, die mathematischen Objekten zugeordnet sind, die als elliptische Kurven bezeichnet werden. Es gibt Regeln für das Hinzufügen und Berechnen von Vielfachen dieser Zahlen, genau wie für Zahlen modulo p.,
ECC enthält Varianten vieler kryptographischer Schemata, die ursprünglich für modulare Zahlen wie ElGamal-Verschlüsselung und digitaler Signaturalgorithmus entwickelt wurden.
Es wird angenommen, dass das Problem des diskreten Logarithmus viel schwieriger ist, wenn es auf Punkte auf einer elliptischen Kurve angewendet wird. Dies fordert das Umschalten von Zahlen Modulo p zu Punkten auf einer elliptischen Kurve auf. Auch eine äquivalente Sicherheitsstufe kann mit kürzeren Schlüsseln erhalten werden, wenn wir elliptische kurvenbasierte Varianten verwenden.,
Die kürzeren Schlüssel führen zu zwei Vorteilen –
- Einfache Schlüsselverwaltung
- Effiziente Berechnung
Diese Vorteile machen elliptisch-kurvenbasierte Varianten des Verschlüsselungsschemas für Anwendungen mit eingeschränkten Rechenressourcen sehr attraktiv.
RSA-und ElGamal-Schemata-Ein Vergleich
Lassen Sie uns kurz die RSA-und ElGamal-Schemata zu den verschiedenen Aspekten vergleichen.
| RSA | ElGamal |
|---|---|
| Es ist mehr effiziente für die Verschlüsselung. | Es ist effizienter für die Entschlüsselung., |
| Es ist weniger effizient für die Entschlüsselung. | Es ist effizienter für die Entschlüsselung. |
| Für eine bestimmte Sicherheitsstufe sind in RSA lange Schlüssel erforderlich. | Für die gleiche Sicherheitsstufe sind sehr kurze Schlüssel erforderlich. |
| Es ist weit akzeptiert und verwendet. | Es ist neu und nicht sehr beliebt in Markt. |