badania korelacyjne: poszukiwanie relacji między zmiennymi
w przeciwieństwie do badań opisowych, które mają na celu przede wszystkim dostarczenie statycznych obrazów, badania korelacyjne obejmują pomiar dwóch lub więcej istotnych zmiennych i ocenę zależności między tymi zmiennymi lub między nimi., Na przykład, zmienne wysokości i wagi są systematycznie powiązane (skorelowane), ponieważ ludzie wyżsi zazwyczaj ważą więcej niż krótszych ludzi. W ten sam sposób powiązane są również błędy czasu nauki i pamięci, ponieważ im więcej czasu dana osoba ma na zbadanie listy słów, tym mniej błędów popełni. Gdy w projekcie badawczym występują dwie zmienne, jedna z nich nazywana jest zmienną predykcyjną, a druga zmienną wyniku., Projekt badawczy można wizualizować w ten sposób, gdzie zakrzywiona strzałka reprezentuje oczekiwaną korelację między dwiema zmiennymi:
rysunek 2.2.2

jednym ze sposobów organizowania danych z badania korelacyjnego z dwoma zmiennymi jest wykresy wartości każdej ze zmierzonych zmiennych za pomocą wykresu punktowego. Jak widać na rysunku 2.10 „przykłady Wykresów punktowych”, wykres punktowy jest wizualnym obrazem relacji między dwiema zmiennymi., Punkt jest wykreślany dla każdej osoby na przecięciu jej punktów dla dwóch zmiennych. Gdy związek między zmiennymi na wykresie punktowym można łatwo aproksymować linią prostą, jak w częściach (a) i (b) rysunku 2.10 „przykłady Wykresów punktowych”, zmienne mówi się, że mają liniową zależność.
gdy linia prosta wskazuje, że osoby, które mają ponadprzeciętne wartości dla jednej zmiennej, również mają Powyżej średniej wartości dla drugiej zmiennej, jak w części (a), relacja mówi się, że jest dodatnia liniowa., Przykłady pozytywnych zależności liniowych obejmują te między wzrostem i wagą, między wykształceniem a dochodem, a między wiekiem a zdolnościami matematycznymi u dzieci. W każdym przypadku ludzie, którzy uzyskują wyższe wyniki na jednej ze zmiennych, również mają tendencję do uzyskiwania wyższych wyników na drugiej zmiennej. Ujemne zależności liniowe, natomiast, jak pokazano w części (b), występują, gdy wartości powyżej średniej dla jednej zmiennej wydają się być związane z wartościami poniżej średniej dla drugiej zmiennej., Przykłady negatywnych zależności liniowych obejmują te między wiekiem dziecka a liczbą pieluch, których dziecko używa, oraz między ćwiczeniami i błędami popełnionymi w zadaniu edukacyjnym. W tych przypadkach osoby, które uzyskują wyższe wyniki na jednej ze zmiennych, mają tendencję do uzyskiwania niższych wyników na drugiej zmiennej.
relacje między zmiennymi, których nie można opisać linią prostą, są znane jako relacje nieliniowe. Część (c) rysunku 2.10 „przykłady Wykresów punktowych” pokazuje wspólny wzór, w którym rozkład punktów jest zasadniczo losowy., W tym przypadku nie ma żadnego związku między tymi dwiema zmiennymi i mówi się, że są one niezależne. Części (d) i (e)rysunku 2.10 „przykłady Wykresów rozrzutu” pokazują wzory asocjacji, w których, chociaż istnieje skojarzenie, punkty nie są dobrze opisane przez jedną prostą. Na przykład część (d) pokazuje Rodzaj relacji, która często występuje między lękiem a wydajnością., Wzrost lęku od niskiego do umiarkowanego poziomu są związane ze wzrostem wydajności, podczas gdy wzrost lęku od umiarkowanego do wysokiego poziomu są związane ze spadkiem wydajności. Relacje, które zmieniają się w kierunku, a tym samym nie są opisane przez pojedynczą linię prostą, nazywane są relacjami krzywoliniowymi.
rysunek 2.10 przykłady Wykresów punktowych
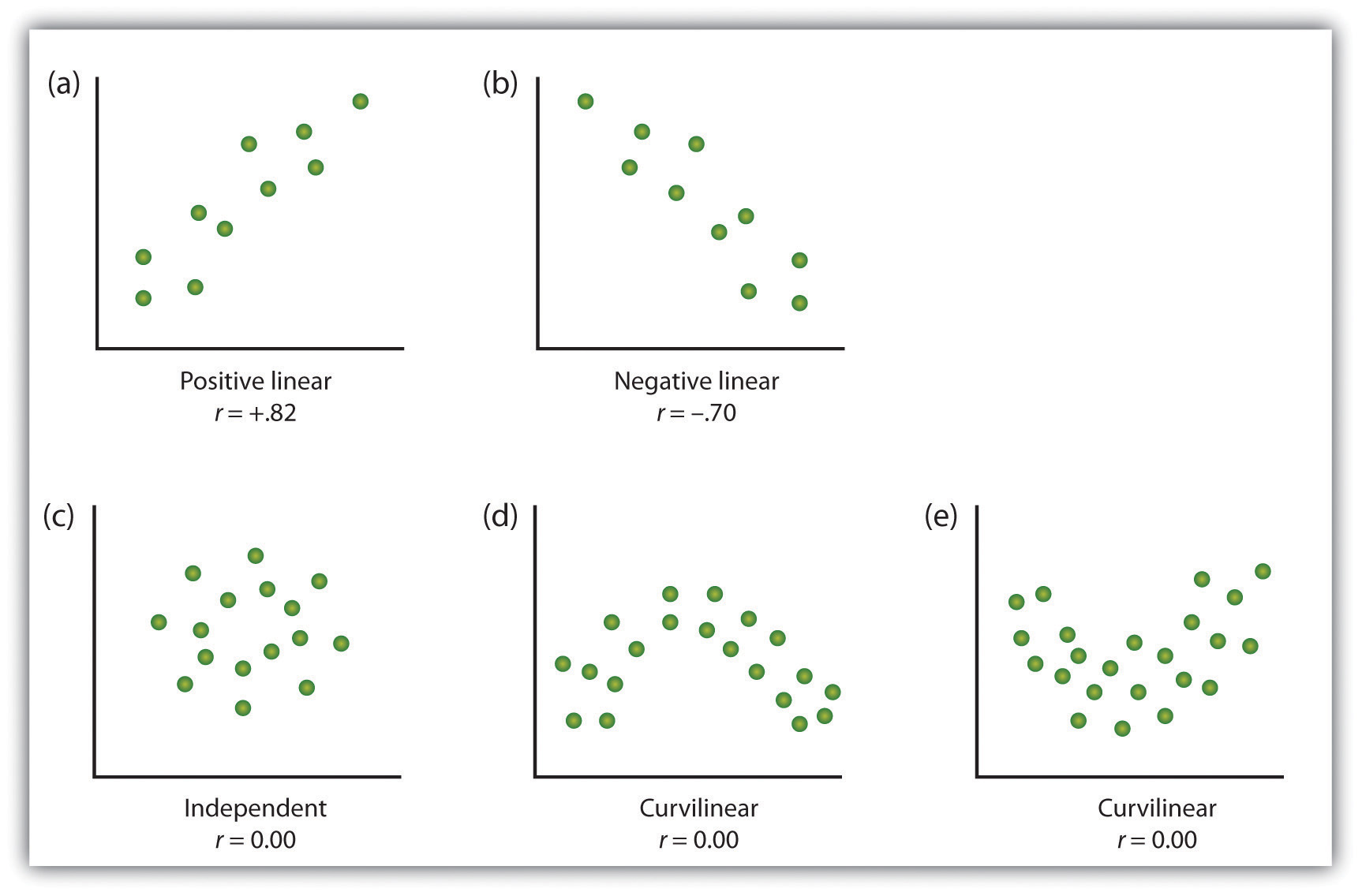
niektóre przykłady relacji między dwiema zmiennymi, jak pokazano na wykresach punktowych., Należy zauważyć, że współczynnik korelacji Pearsona (R) między zmiennymi, które mają relacje krzywoliniowe, będzie prawdopodobnie bliski zeru.
Metody badawcze w naukach behawioralnych (wyd.). Mountain View, CA: Cengage.
najczęstszą statystyczną miarą siły zależności liniowych między zmiennymi jest współczynnik korelacji Pearsona, który jest symbolizowany literą r. wartość współczynnika korelacji waha się od r = -1,00 do R = +1,00., Kierunek zależności liniowej wskazuje znak współczynnika korelacji. Dodatnie wartości r (np. r = .54 lub r = .67) wskazują, że zależność jest dodatnia liniowa (tzn. wzór kropek na wykresie punktowym biegnie od dolnego lewego do górnego prawego), podczas gdy wartości ujemne r (takie jak r = –.30 lub r = -.72) wskazują ujemne zależności liniowe(tzn. kropki biegną od lewego górnego rogu do prawego dolnego rogu). Siła zależności liniowej jest indeksowana przez odległość współczynnika korelacji od zera (jego wartość bezwzględna)., Na przykład r=–.54 jest silniejszą relacją niż r = .30 i r = .72 jest silniejszą relacją niż r=–.57. Ponieważ współczynnik korelacji Pearsona mierzy tylko relacje liniowe, zmienne, które mają relacje krzywoliniowe, nie są dobrze opisane przez r, A obserwowana korelacja będzie bliska zeru.
Możliwe jest również badanie relacji między więcej niż dwoma miarami w tym samym czasie., Projekt badawczy, w którym więcej niż jedna zmienna predyktora jest używana do przewidywania pojedynczej zmiennej wyniku jest analizowana poprzez wielokrotną regresję (Aiken & West, 1991). Regresja wielokrotna jest techniką statystyczną, opartą na współczynnikach korelacji między zmiennymi, która umożliwia przewidywanie pojedynczej zmiennej wyniku z więcej niż jednej zmiennej predykcyjnej. Na przykład rysunek 2.11 „Przewidywanie wydajności pracy z trzech zmiennych predykcyjnych” pokazuje wielokrotną analizę regresji, w której trzy zmienne predykcyjne są używane do przewidywania pojedynczego wyniku., Zastosowanie wielokrotnej analizy regresji pokazuje ważną zaletę korelacyjnych projektów badawczych—mogą być używane do przewidywania na temat osoby prawdopodobny wynik na zmiennej wyniku (np wydajność pracy) w oparciu o wiedzę o innych zmiennych.
rysunek 2.11 Przewidywanie wydajności pracy na podstawie trzech zmiennych predykcyjnych
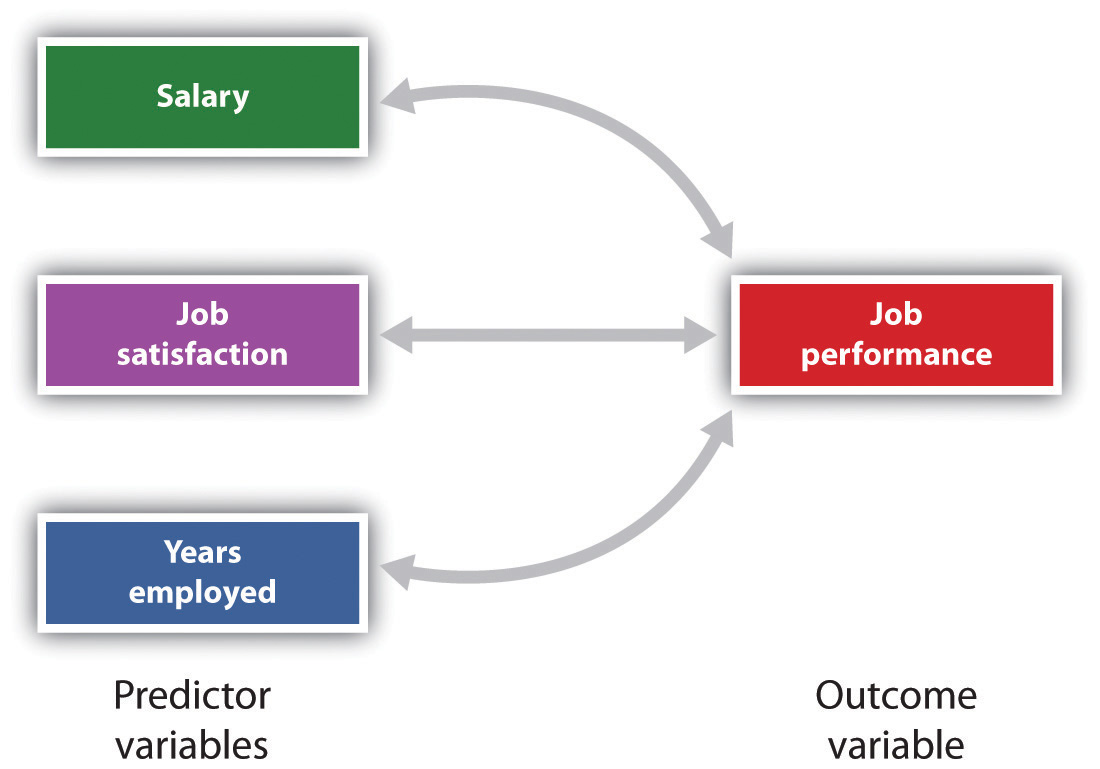
regresja wielokrotna pozwala naukowcom przewidzieć wyniki na jednej zmiennej wyniku przy użyciu więcej niż jednego predykatora zmienna.,
ważnym ograniczeniem korelacyjnych projektów badawczych jest to, że nie można ich wykorzystać do wyciągania wniosków na temat związków przyczynowych między mierzonymi zmiennymi. Rozważ na przykład badacza, który postawił hipotezę, że oglądanie gwałtownych zachowań spowoduje zwiększoną agresywną zabawę u dzieci. Na podstawie próbki dzieci z czwartej klasy zebrał miarę liczby brutalnych programów telewizyjnych, które każde dziecko ogląda w ciągu tygodnia, a także miarę tego, jak agresywnie każde dziecko gra na szkolnym placu zabaw., Na podstawie zebranych danych badacz odkrywa pozytywną korelację między dwiema mierzonymi zmiennymi.
chociaż ta pozytywna korelacja wydaje się potwierdzać hipotezę badacza, nie można uznać, że oglądanie gwałtownej telewizji powoduje agresywne zachowania. Chociaż badacz skusi się na założenie, że oglądanie brutalnej telewizji powoduje agresywną grę,
rysunek 2.2.2

są inne możliwości., Alternatywną możliwością jest to, że kierunek przyczynowy jest dokładnie przeciwny od tego, co zostało postawione hipotezy. Być może dzieci, które zachowywały się agresywnie w szkole, rozwijają pozostałą ekscytację, która sprawia, że chcą oglądać brutalne programy telewizyjne w domu:
rysunek 2.2.2

chociaż ta możliwość może wydawać się mniej prawdopodobna, nie ma sposobu, aby wykluczyć możliwość takiego odwrotnego związku przyczynowego na podstawie tej obserwowanej korelacji., Możliwe jest również, że oba kierunki przyczynowe działają i że dwie zmienne powodują siebie nawzajem:
rysunek 2.2.2

jeszcze innym możliwym wyjaśnieniem obserwowanej korelacji jest to, że została ona wytworzona przez obecność wspólnej zmiennej przyczynowej (znanej również jako trzecia zmienna)., Zmienna przyczynowo-przyczynowa to zmienna, która nie jest częścią hipotezy badawczej, ale powoduje zarówno predyktor, jak i zmienną wyniku, a tym samym powoduje obserwowaną korelację między nimi. W naszym przykładzie potencjalną zmienną przyczynowo-przyczynową jest styl dyscypliny rodziców dzieci. Rodzice stosujący surową i karną dyscyplinę mogą produkować dzieci, które lubią oglądać brutalną telewizję i zachowują się agresywnie w porównaniu z dziećmi, których rodzice stosują mniej surową dyscyplinę:
rysunek 2.2.,2
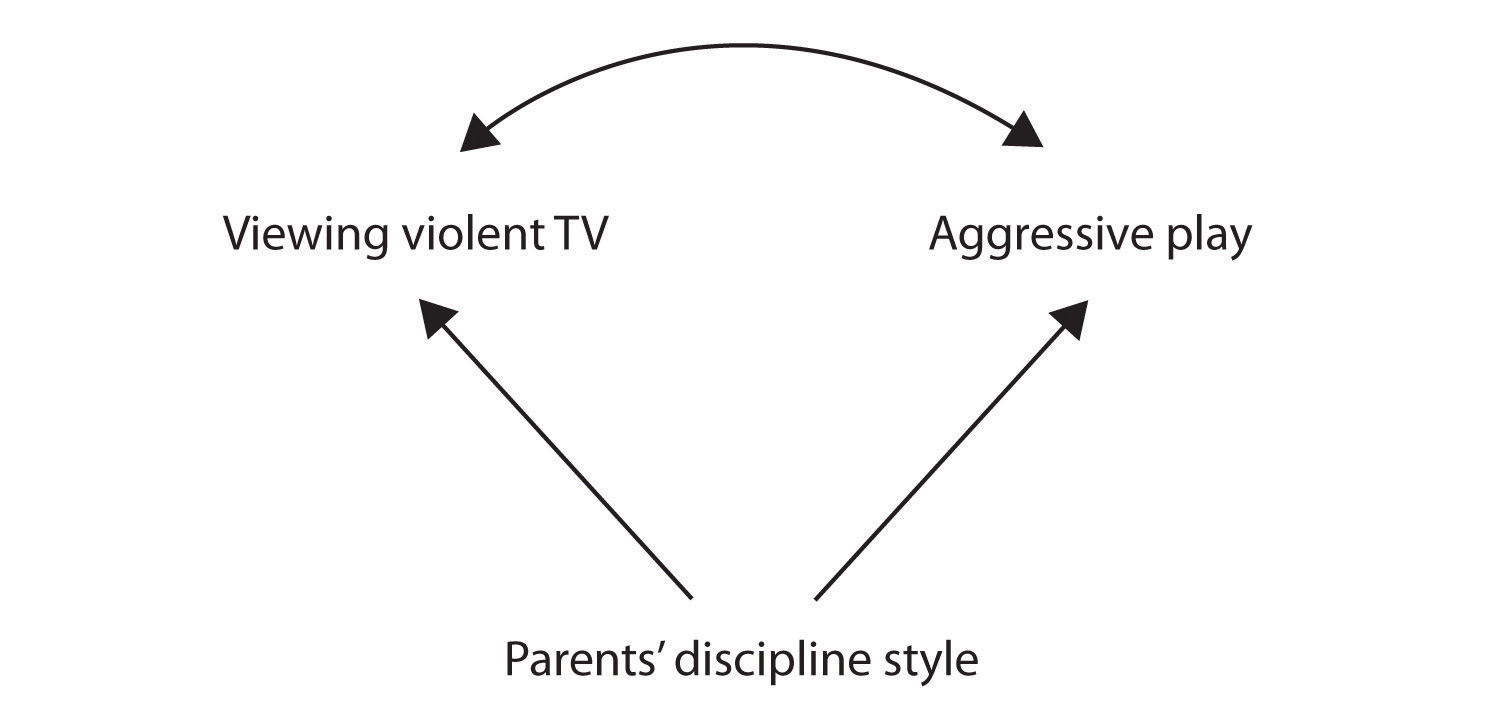
w tym przypadku oglądanie telewizji i agresywna gra byłyby pozytywnie skorelowane (jak wskazuje krzywa strzałka między nimi), mimo że żaden z nich nie spowodował drugiego, ale oba były spowodowane przez styl dyscypliny rodziców (proste strzałki). Gdy predyktor i zmienne wynikowe są zarówno spowodowane przez wspólną zmienną przyczynową, obserwowany związek między nimi mówi się, że jest fałszywy., Sfałszowana relacja jest relacją między dwiema zmiennymi, w której zmienna przyczynowo-skutkowa wytwarza i” wyjaśnia ” związek. Jeśli efekty wspólnej zmiennej przyczynowej zostały usunięte, lub kontrolowane dla, związek między predyktorem i zmiennych wyniku zniknie. W przykładzie związek między agresją a oglądaniem telewizji może być fałszywy, ponieważ kontrolując efekt dyscyplinowania rodziców, związek między oglądaniem telewizji a agresywnym zachowaniem może odejść.,
zmienne przyczynowo-przyczynowe w korelacyjnych projektach badawczych można uznać za zmienne „tajemnicze”, ponieważ, ponieważ nie zostały zmierzone, ich obecność i tożsamość są zwykle nieznane badaczowi. Ponieważ nie jest możliwe zmierzenie każdej zmiennej, która mogłaby spowodować zarówno predyktor, jak i zmienne wyniku, istnienie nieznanej zmiennej common-causal jest zawsze możliwe. Z tego powodu pozostaje nam podstawowe ograniczenie badań korelacyjnych: korelacja nie wykazuje związku przyczynowego., Ważne jest, aby czytając o korelacyjnych projektach badawczych, pamiętać o możliwości fałszywych relacji i należy odpowiednio zinterpretować wyniki. Chociaż badania korelacyjne są czasami zgłaszane jako wykazujące przyczynowość bez wzmianki o możliwości odwrotnej przyczynowości lub wspólnych zmiennych przyczynowych, świadomi konsumenci badań, jak ty, są świadomi tych problemów interpretacyjnych.
podsumowując, korelacyjne projekty badawcze mają zarówno mocne, jak i ograniczenia., Jedną z zalet jest to, że można je stosować, gdy badania eksperymentalne nie są możliwe, ponieważ zmienne predykcyjne nie mogą być manipulowane. Projekty korelacyjne mają również tę zaletę, że pozwalają badaczowi badać zachowanie, które występuje w życiu codziennym. Możemy również korzystać z projektów korelacyjnych do przewidywania-na przykład, aby przewidzieć na podstawie wyników z ich baterii testów sukces stażystów podczas sesji szkoleniowej. Nie możemy jednak wykorzystywać takich korelacyjnych informacji do określenia, czy szkolenie spowodowało lepsze wyniki w pracy. W tym celu naukowcy polegają na eksperymentach.,