Kryptografia klucza publicznego
kryptografii, nie znajdujemy Historycznego wykorzystania kryptografii klucza publicznego. Jest to stosunkowo nowa koncepcja.
Kryptografia symetryczna była dobrze dostosowana do organizacji takich jak rządy, wojsko i wielkie korporacje finansowe były zaangażowane w tajną komunikację.,
wraz z rozpowszechnieniem się w ostatnich dziesięcioleciach bardziej niezabezpieczonych sieci komputerowych, odczuwalna była prawdziwa potrzeba wykorzystania kryptografii na większą skalę. Klucz symetryczny okazał się niepraktyczny ze względu na wyzwania, z jakimi borykał się w zarządzaniu kluczami. To dało początek kryptosystemom klucza publicznego.
proces szyfrowania i deszyfrowania jest przedstawiony na poniższej ilustracji −
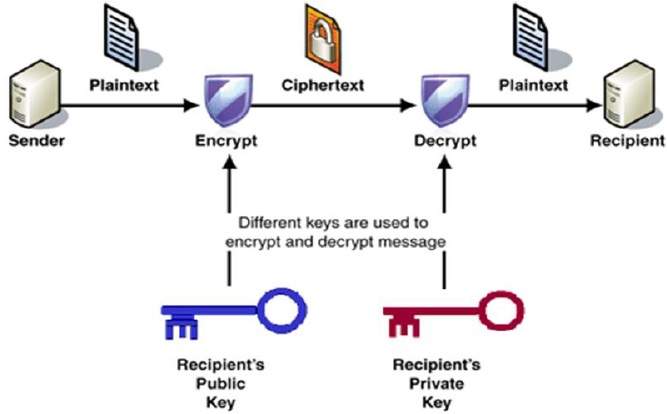
najważniejsze właściwości schematu szyfrowania klucza publicznego to −
-
różne klucze są używane do szyfrowania i deszyfrowania., Jest to właściwość, która ustawia ten schemat inny niż schemat szyfrowania symetrycznego.
-
każdy odbiornik posiada unikalny klucz deszyfrujący, ogólnie określany jako jego klucz prywatny.
-
odbiorca musi opublikować klucz szyfrowania, zwany jego kluczem publicznym.
-
w tym schemacie potrzebne jest pewne zapewnienie autentyczności klucza publicznego, aby uniknąć fałszowania przez przeciwnika jako odbiorcę. Ogólnie rzecz biorąc, ten typ kryptosystem obejmuje zaufaną stronę trzecią, która poświadcza, że dany klucz publiczny należy tylko do określonej osoby lub podmiotu.,
-
algorytm szyfrowania jest na tyle skomplikowany, że uniemożliwia atakującemu wyciągnięcie tekstu jawnego z szyfru i klucza szyfrowania (publicznego).
-
chociaż klucze prywatne i publiczne są powiązane matematycznie, nie jest możliwe obliczenie klucza prywatnego z klucza publicznego. W rzeczywistości inteligentną częścią każdego kryptosystemu klucza publicznego jest projektowanie relacji między dwoma kluczami.
istnieją trzy typy schematów szyfrowania kluczy publicznych., Omawiamy je w poniższych sekcjach-
RSA Cryptosystem
Ten kryptosystem jest jednym z systemów początkowych. Do dziś pozostaje najczęściej stosowanym kryptosystemem. System został wynaleziony przez trzech uczonych Rona Rivesta, Adi Shamira i Lena Adlemana i stąd nazywany jest kryptosystemem RSA.
zobaczymy dwa aspekty kryptosystemu RSA, po pierwsze generowanie pary kluczy, a po drugie algorytmy szyfrująco-deszyfrujące.,
generowanie pary kluczy RSA
każda osoba lub strona pragnąca uczestniczyć w komunikacji za pomocą szyfrowania musi wygenerować parę kluczy, a mianowicie klucz publiczny i klucz prywatny. Proces generowania kluczy jest opisany poniżej −
-
Wygeneruj moduł RSA (n)
-
wybierz dwie duże liczby pierwsze, p i q.
-
Oblicz N=P*q. dla silnego, niełamliwego szyfrowania, niech N będzie dużą liczbą, zazwyczaj minimum 512 bitów.,
-
-
Znajdź liczbę pochodną (e)
-
Liczba e musi być większa niż 1 i mniejsza niż (P − 1)(q − 1).
-
nie może być wspólnego czynnika dla e I (p − 1)(q − 1) z wyjątkiem 1. Innymi słowy dwie liczby e I (p – 1)(q – 1) są koprimami.
-
-
tworzy klucz publiczny
-
Para liczb (n, e) tworzy klucz publiczny RSA i jest upubliczniana.,
-
Co ciekawe, chociaż n jest częścią klucza publicznego, trudności w faktorowaniu dużej liczby pierwszej zapewniają, że atakujący nie może znaleźć w skończonym czasie dwóch liczb pierwszych (p & q) używanych do uzyskania N. Jest to siła RSA.
-
-
generuje klucz prywatny
-
klucz prywatny D jest obliczany z p, q i e. dla podanych n i e istnieje unikalna liczba d.
-
Liczba d jest odwrotnością modulo e (p – 1)(q – 1)., Oznacza to, że d jest liczbą mniejszą od (p-1) (q-1) taką, że pomnożona przez e jest równa 1 modulo (P-1) (q-1).
-
zależność ta jest zapisana matematycznie w następujący sposób −
-
ed = 1 mod (p − 1)(q − 1)
Rozszerzony algorytm Euklidesowy przyjmuje p, q i e jako wejście i daje d jako wyjście.
przykład
przykład generowania pary kluczy RSA podano poniżej. (Dla ułatwienia zrozumienia, liczby pierwsze p & Q wzięte tutaj są małymi wartościami. Praktycznie wartości te są bardzo wysokie).,
-
niech dwie liczby pierwsze będą p = 7 i q = 13. Zatem moduł N = pq = 7 x 13 = 91.
-
Wybierz e = 5, który jest prawidłowym wyborem, ponieważ nie ma liczby, która jest wspólnym czynnikiem 5 I(P-1) (q− 1) = 6 × 12 = 72, Z wyjątkiem 1.
-
Para liczb (n, e) = (91, 5) tworzy klucz publiczny i może być udostępniona każdemu, komu chcemy wysyłać do nas zaszyfrowane wiadomości.
-
Wejście p = 7, q = 13 i e = 5 do rozszerzonego algorytmu Euklidesowego. Wyjście będzie d = 29.,
-
sprawdź, czy obliczony d jest poprawny przez obliczenie −
de = 29 × 5 = 145 = 1 mod 72
-
stąd, kluczem publicznym jest (91, 5), a kluczem prywatnym (91, 29).
szyfrowanie i deszyfrowanie
po wygenerowaniu pary kluczy proces szyfrowania i deszyfrowania jest stosunkowo prosty i łatwy obliczeniowo.
Co ciekawe, RSA nie działa bezpośrednio na ciągach bitów, jak w przypadku symetrycznego szyfrowania kluczy. Operuje on na liczbach modulo N. dlatego konieczne jest reprezentowanie tekstu jawnego jako szeregu liczb mniejszych niż N.,
szyfrowanie RSA
-
Załóżmy, że nadawca chce wysłać wiadomość tekstową do kogoś, kto ma klucz publiczny (n, e).
-
nadawca przedstawia tekst jawny jako serię liczb mniejszych niż n.
-
aby zaszyfrować pierwszy tekst jawny P, który jest liczbą modulo N. proces szyfrowania jest prosty matematyczny krok jako −
C = Pe mod n
-
innymi słowy, tekst zaszyfrowany C jest równy do zwykłego tekstu p pomnożonego przez siebie e razy, a następnie zredukowanego modulo n. oznacza to, że C jest również liczbą mniejszą od N.,
-
Wracając do naszego przykładu generowania kluczy ze zwykłym tekstem P = 10, otrzymujemy tekst szyfrowy C −
C = 105 mod 91
odszyfrowywanie RSA
-
proces odszyfrowywania RSA jest również bardzo prosty. Załóżmy, że odbiornik pary kluczy publicznych (n, e) otrzymał tekst szyfrowy C.
-
Odbiornik podnosi C do mocy swojego klucza prywatnego d. wynikiem modulo n będzie tekst jawny P.,
Plaintext = Cd mod n
-
Wracając do naszego przykładu numerycznego, zaszyfrowany tekst C = 82 zostanie zaszyfrowany do numeru 10 przy użyciu klucza prywatnego 29 −
Plaintext = 8229 mod 91 = 10
Analiza RSA
bezpieczeństwo RSA zależy od zalet dwóch oddzielnych funkcji. Najpopularniejszym kryptosystemem RSA jest kryptosystem klucza publicznego, którego siła opiera się na praktycznej trudności faktoringu bardzo dużych liczb.,
-
funkcja szyfrowania − jest uważana za funkcję jednokierunkową przekształcania tekstu jawnego w tekst szyfrowy i może być odwrócona tylko ze znajomością klucza prywatnego d.
-
Generowanie klucza-trudność określenia klucza prywatnego z klucza publicznego RSA jest równoważna faktorowaniu modułu N. atakujący nie może więc użyć znajomości klucza publicznego RSA do określenia klucza prywatnego RSA, chyba że potrafi uwzględnić N. Jest to również funkcja jednokierunkowa, idąca od p
-
div id=”3db477d92a” >
wartości q do modułu N jest łatwe, ale odwrócenie nie jest możliwe. ,
jeśli któraś z tych dwóch funkcji okaże się nie jednokierunkowa, to RSA zostanie przerwana. W rzeczywistości, jeśli technika efektywnego faktoringu zostanie opracowana, RSA nie będzie już bezpieczny.
siła szyfrowania RSA drastycznie spada przed atakami, jeśli liczba p i q nie są dużymi liczbami pierwszymi i / lub wybrany klucz publiczny e jest małą liczbą.
Elgamal Cryptosystem
wraz z RSA, istnieją inne kryptosystemy klucza publicznego proponowane. Wiele z nich opiera się na różnych wersjach problemu logarytmu dyskretnego.,
kryptosystem Elgamala, zwany wariantem krzywej eliptycznej, opiera się na problemie logarytmu dyskretnego. Wynika ona z założenia, że logarytmów dyskretnych nie można znaleźć w praktycznym przedziale czasowym dla danej liczby, natomiast odwrotna operacja potęgi może być efektywnie obliczona.
przejdźmy do prostej wersji Elgamala, która działa z liczbami modulo p. w przypadku wariantów krzywych eliptycznych opiera się na zupełnie innych systemach liczbowych.,
generowanie pary kluczy ElGamal
każdy użytkownik ElGamal cryptosystem generuje parę kluczy w następujący sposób −
-
wybierając dużą liczbę pierwszą. zazwyczaj wybierana jest liczba pierwsza o długości od 1024 do 2048 bitów.
-
Wybór elementu generatora g.
-
ta liczba musi być pomiędzy 1 A p − 1, ale nie może być żadną liczbą.
-
jest generatorem multiplikatywnej grupy liczb całkowitych modulo P. oznacza to, że dla każdej liczby całkowitej m współmiernej do p, istnieje liczba całkowita k taka, że gk=a mod n.,
np. 3 jest generatorem grupy 5 (Z5 = {1, 2, 3, 4}).
-
| N | 3N | 3N mod 5 |
|---|---|---|
| 1 | 3 | |
| 2 td | 9 | 4 |
| 3 | 27 | 2 |
| 4 | 81 | 1 |
-
wybór klucza prywatnego. Klucz prywatny x to dowolna liczba większa od 1 i mniejsza od p−1.
-
część obliczeniowa klucza publicznego., Wartość y jest obliczana z parametrów p, g i klucza prywatnego x w następujący sposób −
y = gx mod p
-
uzyskanie klucza publicznego. Klucz publiczny ElGamal składa się z trzech parametrów (p, g, y).
na przykład załóżmy, że p = 17 i że g = 6 (można potwierdzić, że 6 jest generatorem grupy Z17). Klucz prywatny x może być dowolną liczbą większą niż 1 i mniejszą niż 71, więc wybieramy x = 5. Wartość y jest następnie obliczana w następujący sposób −
y = 65 mod 17 = 7
-
tak więc kluczem prywatnym jest 62, a kluczem publicznym (17, 6, 7).,
szyfrowanie i deszyfrowanie
generowanie pary kluczy ElGamal jest stosunkowo prostsze niż równoważny proces RSA. Ale szyfrowanie i deszyfrowanie są nieco bardziej złożone niż RSA.
Szyfrowanie ElGamal
Załóżmy, że nadawca chce wysłać tekst jawny do kogoś, kto ma klucz publiczny ElGamal (p, g, y), a następnie −
-
nadawca reprezentuje tekst jawny jako serię liczb modulo p.
-
aby zaszyfrować pierwszy tekst jawny P, który jest reprezentowany jako liczba modulo P., Proces szyfrowania w celu uzyskania szyfrogramu C wygląda następująco-
- losowo generuje liczbę k;
- oblicza dwie wartości C1 i C2, gdzie −
C1 = gk mod pC2 = (P*yk) mod p
-
wysyła szyfrogram C, składający się z dwóch oddzielnych wartości (C1, C2), wysyłanych razem.,
-
odnosząc się do powyższego przykładu generowania kluczy ElGamal, tekst jawny P = 13 jest szyfrowany w następujący sposób −
- losowo generuje liczbę, powiedzmy k = 10
- Oblicz dwie wartości C1 i C2, gdzie −
C1 = 610 mod 17C2 = (13*710) mod 17 = 9
-
wyślij zaszyfrowany tekst C = (C1, C2) = (15, 9).,
odszyfrowywanie Elgamalu
-
aby odszyfrować szyfrogram (C1, C2) za pomocą klucza prywatnego X, należy wykonać następujące dwa kroki −
-
Oblicz modularną odwrotność (C1)x modulo P, która jest (C1)-x , ogólnie określana jako współczynnik deszyfrowania.,
-
uzyskaj tekst jawny za pomocą następującego wzoru −
-
C2 × (C1)-x mod p = Plaintext
-
w naszym przykładzie, aby odszyfrować tekst szyfrowy C = (C1, C2) = (15, 9) za pomocą klucza prywatnego x = 5, współczynnik deszyfrowania wynosi
15-5 mod 17 = 9
-
wyodrębnij tekst zwykły p = (9 × 9) mod 17 = 13.
Analiza ElGamal
w systemie Elgamal każdy użytkownik ma klucz prywatny x. i ma trzy składniki klucza publicznego − moduł prime p, generator g i publiczny y = GX mod p., Siła Elgamalu opiera się na trudnościach problemu logarytmu dyskretnego.
rozmiar bezpiecznego klucza wynosi zazwyczaj > 1024 bity. Obecnie używa się nawet 2048 bitów długiego klucza. Jeśli chodzi o szybkość przetwarzania, Elgamal jest dość powolny, jest używany głównie do kluczowych protokołów uwierzytelniania. Ze względu na wyższą wydajność przetwarzania, warianty krzywych eliptycznych Elgamal stają się coraz bardziej popularne.,
Elliptic Curve Cryptography (ECC)
Elliptic Curve Cryptography (ECC) to termin używany do opisania zestawu narzędzi kryptograficznych i protokołów, których bezpieczeństwo opiera się na specjalnych wersjach problemu logarytmu dyskretnego. Nie używa liczb modulo p.
ECC opiera się na zbiorach liczb, które są związane z obiektami matematycznymi zwanymi krzywymi eliptycznymi. Istnieją zasady dodawania i obliczania wielokrotności tych liczb, tak jak istnieją dla liczb modulo P.,
ECC zawiera warianty wielu schematów kryptograficznych, które początkowo były przeznaczone dla numerów modularnych, takich jak szyfrowanie ElGamal i algorytm podpisu cyfrowego.
uważa się, że problem logarytmu dyskretnego jest znacznie trudniejszy, gdy stosuje się go do punktów na krzywej eliptycznej. Powoduje to przejście z liczb modulo p do punktów na krzywej eliptycznej. Również równoważny poziom bezpieczeństwa można uzyskać z krótszymi kluczami, jeśli używamy wariantów opartych na krzywej eliptycznej.,
krótsze klucze dają dwie korzyści −
- łatwość zarządzania kluczami
- wydajne obliczenia
te korzyści sprawiają, że warianty szyfrowania oparte na krzywych eliptycznych są bardzo atrakcyjne dla aplikacji, w których zasoby obliczeniowe są ograniczone.
Schematy RSA i ElGamal – porównanie
porównajmy krótko Schematy RSA i ElGamal w różnych aspektach.
| RSA | ElGamal |
|---|---|
| jest bardziej wydajny dla szyfrowania. | jest bardziej wydajny do deszyfrowania., |
| jest mniej wydajny do deszyfrowania. | jest bardziej wydajny do deszyfrowania. |
| dla określonego poziomu bezpieczeństwa wymagane są długie klucze w RSA. | dla tego samego poziomu bezpieczeństwa wymagane są bardzo krótkie klucze. |
| jest powszechnie akceptowane i stosowane. | jest nowy i niezbyt popularny na rynku. |