prawdopodobieństwo
cele uczenia się
· Zdefiniuj Zdarzenie, wynik, próbę, Zdarzenie proste, przestrzeń próbki i Oblicz prawdopodobieństwo wystąpienia zdarzenia.
· Oblicz prawdopodobieństwo zdarzeń dla bardziej złożonych wyników.
· rozwiązywanie aplikacji dotyczących prawdopodobieństwa.
wprowadzenie
prawdopodobieństwo dostarcza miary prawdopodobieństwa, że coś się wydarzy., Jest to liczba między liczbami 0 i 1 włącznie. Może być zapisany jako ułamek, dziesiętny lub procent.

losowanie numerów losowo oznacza, że nie ma określonej kolejności, w której są wybierane. Wiele gier używa kości lub spinnerów do generowania liczb losowo. Jeśli rozumiesz, jak obliczać prawdopodobieństwo, możesz podejmować przemyślane decyzje dotyczące sposobu grania w te gry, znając prawdopodobieństwo różnych wyników.,
definicje
najpierw musisz znać pewne terminy związane z prawdopodobieństwem. Podczas pracy z prawdopodobieństwem losowe działanie lub seria działań nazywa się próbą. Wynik jest wynikiem próby, a zdarzenie jest szczególnym zbiorem wyników. Zdarzenia są zwykle opisywane przy użyciu wspólnej cechy wyników.
zastosujmy ten język, aby zobaczyć, jak terminy działają w praktyce. Niektóre gry wymagają toczenia matrycy z sześcioma stronami, ponumerowanymi od 1 do 6. (Dice jest liczbą mnogą od die.,) Poniższy wykres ilustruje użycie próby, wyniku i zdarzenia dla takiej gry:
zauważ, że zbiór wyników jest umieszczany w klamrach i oddzielany przecinkami.
Zdarzenie proste to zdarzenie z tylko jednym wynikiem. Rzut 1 byłby prostym wydarzeniem, ponieważ działa tylko jeden wynik—1! Przewrócenie więcej niż 5 byłoby również prostym wydarzeniem, ponieważ zdarzenie zawiera tylko 6 jako ważny wynik. Zdarzenie złożone to zdarzenie z więcej niż jednym wynikiem. Na przykład w toczeniu jednej sześciostronnej matrycy może wystąpić liczba parzysta z jednym z trzech wyników: 2, 4 i 6.,
kiedy rzucasz sześciostronną kostkę wiele razy, nie powinieneś oczekiwać, że jakikolwiek wynik wydarzy się częściej niż inny(zakładając, że jest to uczciwa kostka). Wyniki w takiej sytuacji są uważane za równie prawdopodobne. Bardzo ważne jest, aby rozpoznać, kiedy wyniki są równie prawdopodobne przy obliczaniu prawdopodobieństwa. Ponieważ każdy wynik w badaniu walcowania matrycowego jest równie prawdopodobny, można oczekiwać, że każdy wynik ![]() rolek., Oznacza to, że można oczekiwać, że
rolek., Oznacza to, że można oczekiwać, że ![]() rolek będzie 1,
rolek będzie 1, ![]() rolek będzie 2,
rolek będzie 2, ![]() rolek będzie 3, i tak dalej.
rolek będzie 3, i tak dalej.
spinner jest podzielony na cztery równe części, z których każda ma inny kolor, Jak pokazano poniżej. Kiedy ten spinner jest obrócony, strzałka wskazuje na jeden z kolorów. Czy wyniki są równie prawdopodobne?
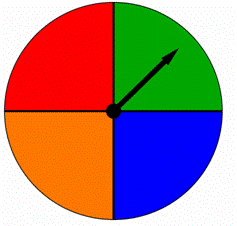
a) tak, są one równie prawdopodobne.
B) nie, nie są równie prawdopodobne.,
prawdopodobieństwo wystąpienia zdarzenia
prawdopodobieństwo wystąpienia zdarzenia określa częstotliwość jego występowania. Jest to stosunek wielkości przestrzeni zdarzeń do wielkości przestrzeni próbki.
najpierw musisz określić rozmiar przestrzeni próbki. Wielkość przestrzeni próbki jest całkowitą liczbą możliwych wyników. Na przykład, gdy wyrzucisz 1 matrycę, przestrzeń próbki jest 1, 2, 3, 4, 5, do 6. Więc wielkość przestrzeni próbki wynosi 6.
następnie należy określić rozmiar przestrzeni zdarzeń., Przestrzeń wydarzenia to liczba wyników w wydarzeniu, które Cię interesuje. Miejsce na wyrzucenie liczby mniejszej niż trzy to 1 lub 2. Więc wielkość przestrzeni eventowej wynosi 2.
Dla równie prawdopodobnych wyników prawdopodobieństwo zdarzenia E można zapisać P(E).
![]()
|
przykład |
||
|
problem |
gra wymaga obracania sześciostronnej matrycy o numerach od 1 do 6., Jakie jest prawdopodobieństwo wyrzucenia liczby parzystej? |
|
|
przestrzeń próbki = {1, 2, 3, 4, 5, 6}
przestrzeń zdarzeń = {2, 4, 6} |
najpierw znajdź przestrzeń próbki i przestrzeń zdarzenia. Przestrzeń próbki to wszystkie możliwe wyniki, a przestrzeń zdarzenia To wyniki w zdarzeniu. W tym przypadku, zdarzenie jest ” rolling liczby parzystej.,” |
|
|
|
ponieważ wyniki są równie prawdopodobne, prawdopodobieństwo zdarzenia jest stosunek przestrzeni zdarzenia do przestrzeni próbki., |
|
|
odpowiedź |
P(numer parzysty) = |
|
powszechną praktyką w przypadku prawdopodobieństwa, podobnie jak w przypadku ułamków, jest uproszczenie prawdopodobieństwa na najniższe terminy, ponieważ ułatwia to większości ludzi poczucie, jak wielkie jest. Jeśli nie ma powodu, aby tego nie robić, wyrażaj wszystkie ostateczne prawdopodobieństwa w najniższych kategoriach.,
spinner jest podzielony na równe części, z których każda ma inny kolor, Jak pokazano poniżej., Znajdź prawdopodobieństwo, że na tym spinnerze zakręci się niebieski lub zielony:
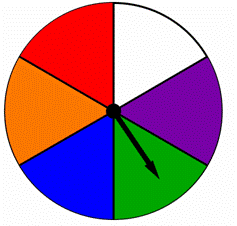
A) ![]()
B) p
c) 2
d) 6
metody liczenia w celu znalezienia przestrzeni próbki
najtrudniejszą rzeczą do obliczenia prawdopodobieństwa może być znalezienie rozmiaru przestrzeni próbki, zwłaszcza jeśli istnieją dwa lub więcej prób. Istnieje kilka metod liczenia, które mogą pomóc.,
pierwszy, który spojrzy na wykres, to wykonanie wykresu. W poniższym przykładzie Tori rzuca dwiema monetami. Więc musisz dokładnie określić przestrzeń próbki. Wykres taki jak ten pokazany w poniższym przykładzie jest dobrym podejściem.
|
przykład |
||
|
Problem |
T |
TT |
sample space: {HH, HT, TH, TT}
event space for 2 heads: {HH}
event space for 1 head: {HT, TH}
Create a chart to record the results of flipping the first coin, followed by the result of flipping the second coin.,
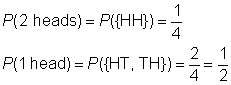
ponieważ wyniki są równie prawdopodobne, prawdopodobieństwo zdarzenia jest stosunek przestrzeni zdarzenia do przestrzeni próbki.,
Odpowiedz
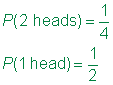
w poniższym przykładzie przestrzeń próbki dla Tori jest prosta, ponieważ tylko jedna matryca jest walcowana. Jednak ponieważ James kręci dwie matryce, Wykres pomaga uporządkować informacje.,
|
przykład |
||||||||
|
Problem |
Tori przewrócił sześciokątną matrycę i chciał uzyskać wynik 1 lub 4. James rzucił dwie sześcioboczne kości, jedną niebieską i jedną czerwoną, i chciał uzyskać wynik zarówno 1, jak i 3, w tym samym czasie. Które zdarzenie ma większe prawdopodobieństwo?, |
|||||||
|
Tori’s sample space: {1, 2, 3, 4, 5, 6}
Tori’s event space: {1, 4}
Tori:
|
First, find the sample space and the event space for the two trials., Proces Tori jest prosty. ponieważ wyniki są równie prawdopodobne, prawdopodobieństwo zdarzenia jest stosunkiem przestrzeni zdarzeń do przestrzeni próbki.,316594724″> 6 |
6,1 |
6,2 |
6,3 |
6,4 |
6,5 |
6,6 |
|
James' sample space has 36 outcomes.,
przestrzeń zdarzeń Jamesa ma 2 wyniki.nie jest to tak oczywiste dla procesu Jamesa, ponieważ rzuca dwiema kostkami. Użyj wykresu, aby znaleźć możliwości.
znaleziono 36 wyników. Z nich jest 2, które mają zarówno 1, jak i 3.,
James: ![]()
ponieważ wyniki są równie prawdopodobne, prawdopodobieństwo zdarzenia jest stosunek przestrzeni zdarzenia do przestrzeni próbki.
odpowiedź
Zdarzenie Tori ma większe prawdopodobieństwo.,
Możesz również użyć diagramu drzewa do określenia przestrzeni próbki. Diagram drzewa ma gałąź dla każdego możliwego wyniku dla każdego zdarzenia.
Załóżmy, że szafa ma trzy pary spodni (czarny, biały i zielony), cztery koszule (zielony, biały, fioletowy i żółty) i dwie pary butów (czarny i biały). Ile różnych strojów można wykonać? Istnieją 3 możliwości wyboru spodni, 4 możliwości wyboru koszul i 2 możliwości wyboru butów., Dla naszego diagramu drzewa, użyjmy B Dla Czarnego, w dla białego, G Dla Zielonego, P dla fioletowego i Y dla żółtego.
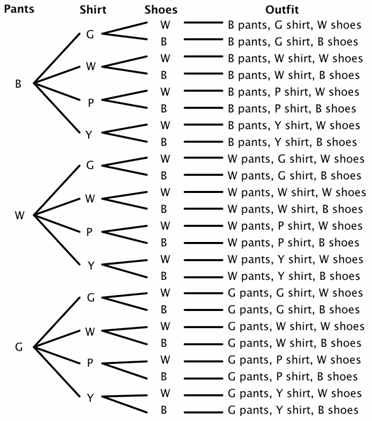
na diagramie drzewa widać, że w przestrzeni próbnej są 24 możliwe stroje (niektóre być może niezbyt dobre wybory).
teraz możesz dość łatwo rozwiązać pewne problemy z prawdopodobieństwem. Na przykład, Jakie jest prawdopodobieństwo, że jeśli zamkniesz oczy i WYBIERZESZ LOSOWO, wybierzesz spodnie i buty w tym samym kolorze? Widać, że jest 8 strojów, w których pasują spodnie i buty.,
![]()
jak już zauważyłeś, gdy próba obejmuje więcej niż jeden losowy element, taki jak rzut więcej niż jedną monetą lub przewrócenie więcej niż jedną kostką, nie zawsze musisz identyfikować każdy wynik w przestrzeni próbnej, aby obliczyć prawdopodobieństwo. Potrzebujesz tylko liczby wyników.
podstawową zasadą liczenia jest sposób na znalezienie liczby wyników bez wymieniania i liczenia każdego z nich.,
podstawowa zasada liczenia
Jeśli jedno zdarzenie ma możliwe wyniki p, a inne Ma możliwe wyniki m, to istnieje suma możliwych wyników p • M dla obu zdarzeń.
przykłady
· rzut dwiema sześciobocznymi kostkami: każda kostka ma 6 równie prawdopodobnych wyników, więc przestrzeń próbki wynosi 6 • 6 lub 36 równie prawdopodobnych wyników.
· rzut trzema monetami: każda moneta ma 2 równie prawdopodobne wyniki, więc przestrzeń próbki jest 2 • 2 • 2 lub 8 równie prawdopodobnych wyników.,
* Toczenie sześciokątnej matrycy i rzut monetą: przestrzeń próbki wynosi 6 * 2 lub 12 równie prawdopodobnych wyników.
więc możesz użyć podstawowej zasady liczenia, aby dowiedzieć się, ile strojów jest w poprzednim przykładzie. Istnieją 3 możliwości wyboru spodni, 4 możliwości wyboru koszul i 2 możliwości wyboru butów. Stosując podstawową zasadę liczenia, masz 4 • 3 • 2 = 24 różne stroje.,
|
przykład |
||
|
Problem |
W każdej torebce wkłada: · jedną z dwóch kanapek (masło orzechowe i galaretka, lub indyk i ser), · jedną z trzech chipsów (zwykłe chipsy ziemniaczane, pieczone chipsy ziemniaczane lub chipsy kukurydziane), · jedną sztukę owoców (jabłka lub pomarańczy)., zapomniał zaznaczyć, co było w torbach. Zakładając, że każdy wybór jest równie prawdopodobny, jakie jest prawdopodobieństwo, że w torbie Therese znajdzie się kanapka z masłem orzechowym, galaretką i jabłkiem?, |
|
|
Size of sample space:
(number of sandwich choices) • (number of chip choices) • (number of fruit choices) = 2 • 3 • 2 = 12
|
First, use the Fundamental Counting Principle to find the size of the sample space., |
|
|
Rozmiar przestrzeni zdarzeń:
(number of Sandwich choices in event) • (number of chip choices in event) • (number of fruit choices in event) = |
dla przestrzeni zdarzeń należy stosować tę samą zasadę. W tym przypadku jest tylko jedna kanapka i jeden owoc zainteresowania, ale każdy z trzech rodzajów chipsów są dopuszczalne., |
|
|
Odpowiedz |
|
użyj współczynnika, aby znaleźć Prawdopodobieństwo. |
Istnieją cztery sposoby na uzyskanie dokładnie jednego ogona: HHHT, HHTH, HTHH i THHH. Jakie jest prawdopodobieństwo, że Carrie dostanie jeden ogon?,
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Summary
Probability helps you understand random, unpredictable situations where multiple outcomes are possible., Jest to miara prawdopodobieństwa zdarzenia, i to zależy od stosunku zdarzenia i możliwych wyników, jeśli wszystkie te wyniki są równie prawdopodobne.