14.5: zasada Pascala i hydraulika

zastosowania zasady Pascala i układów hydraulicznych

możemy wyprowadzić zależność między siłami w tym prostym układzie hydraulicznym stosując zasadę Pascala. Należy najpierw zauważyć, że dwa tłoki w systemie znajdują się na tej samej wysokości, więc nie ma różnicy ciśnień ze względu na różnicę głębokości. Ciśnienie spowodowane przez F1 działające na obszar A1 jest po prostu

\(p_{1} = \frac{F_{1}}{A_{1}}\), zgodnie z definicją \(p = \frac{F}{A}\).,

\

równanie to odnosi się do stosunku siły do powierzchni w dowolnym układzie hydraulicznym, pod warunkiem, że tłoki znajdują się na tej samej wysokości pionowej, a tarcie w układzie jest znikome.

układy hydrauliczne mogą zwiększać lub zmniejszać siłę przyłożoną do nich. Aby zwiększyć siłę, nacisk jest przykładany do większego obszaru. Na przykład, jeśli siła 100 N zostanie przyłożona do lewego cylindra na rysunku 14.16, a prawy cylinder ma obszar pięć razy większy, to siła wyjściowa wynosi 500 N., Układy hydrauliczne są analogiczne do prostych dźwigni, ale mają tę zaletę, że ciśnienie może być przesyłane przez kręte linie do kilku miejsc naraz.

podnośnik hydrauliczny to taki układ hydrauliczny. Podnośnik hydrauliczny służy do podnoszenia ciężkich ładunków, takich jak te używane przez mechaników samochodowych do podnoszenia samochodu. Składa się z nierozpuszczalnego płynu w rurce U wyposażonej w ruchomy tłok z każdej strony. Jedna strona U-rurki jest węższa od drugiej., Mała siła przyłożona na małym obszarze może zrównoważyć znacznie większą siłę po drugiej Stronie na większym obszarze(rysunek \(\PageIndex{3}\)).

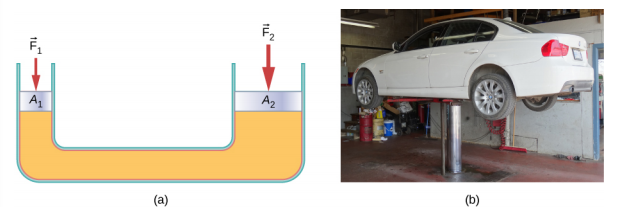
zgodnie z zasadą Pascala można wykazać, że siła potrzebna do podniesienia samochodu jest mniejsza niż masa samochodu:

\

gdzie F1 to siła przyłożona do podniesienia samochodu, A1 to pole przekroju mniejszego tłoka, A2 to pole przekroju większego tłoka, a F2 to masa samochodu.