信頼区間とp値
統計分析の議論を楽しませるためには、まず母集団統計の概念を理解することが重要です。 明らかに、人口統計は、関心のある母集団内の任意の尺度の値であり、それらを推定することは、ほとんどの研究の目標です。, 例えば、特定の投薬を受けている患者の肥満率を調べた研究では、人口統計は投薬を受けているすべての患者の平均肥満率である可能性があります。
ただし、この値を特定するには、このカテゴリに分類されるすべての個人のデータが必要ですが、これは実用的ではありません。 代わりに、無作為化サンプルを収集し、そこからサンプル統計を取得することができます。 これらのサンプル統計は、対応する母集団統計の推定値として機能し、研究者が関心のある母集団について結論を出すことを可能にする。,
これらの構築されたサンプルが関心のあるより大きな母集団を代表しなければならないという点で重要な制限が存在する。 この制限を減らすために取ることができる多くのステップがありますが、時にはその効果(いわゆるサンプリングバイアス)は研究者の制御を超え さらに、サンプリングバイアスのない理論的な状況であっても、ランダム化は誤ったサンプルをもたらす可能性があります。 前の例では、薬物のために資格があるすべての大人間の肥満の人口率が25%だったと仮定して下さい。, この集団からの30人の患者の簡単な無作為試料では、19.7%のチャンスが少なくとも10人の患者が肥満である、33.3%また更に高いサンプル肥満率に終っ 投薬と肥満率との間に関係がなくても、サンプリングのみでランダム性によって生じた全体的な肥満率とは異なるように見える率に遭遇することは依然として可能である。 この効果は、臨床研究における信頼区間およびp値を報告する理由である。
信頼区間は、母集団統計量が存在する可能性のある区間です。, これらは、サンプル統計量およびサンプルの特定の特徴に基づいて構築され、それが代表的である可能性を測定し、特定のしきい値に報告されます。 95%信頼区間とは、平均して、無作為標本の95%が95%信頼区間内に真の母集団統計量を含むように構築された区間です。 したがって、有意な結果のしきい値は、報告された範囲内のすべての値が可能な母集団統計と同等に有効であることを理解して、95%として取られることがよくあります。,
p値は、同様の情報を異なる方法で報告します。 P値は、標本統計量の周りに区間を構築するのではなく、”帰無仮説”と呼ばれる母集団に関する仮定のセットが与えられた母集団の無作為抽出から標本統計量が生成された確率を報告します。, 肥満率に関する例の研究を再び取ると、サンプル(投薬患者のサンプル)間の肥満率は、投薬の対象となる患者の人口全体を無作為にサンプリングすることによって、そのような率が生成される可能性を決定するp値と一緒に報告することができる。 この研究の場合、帰無仮説は、投薬を受けている患者の肥満率が、投薬の対象となるすべての患者の肥満率、すなわち25%に等しいということである。, 片側のp値は、効果が一方向にのみ起こると信じる理由がある場合に使用できます(例えば、投薬が体重増加を増加させるが減少させないと信じる理由 正規分布のような対称分布を使用する場合、両側のp値は単に片側のp値の倍になります。
再び、投薬中の30人の患者のサンプルに12人の肥満者が含まれていると仮定します。 片側検定では、p値は0.0216です(二項分布を使用)。, したがって、観測された40%の割合は、25%の有意水準での仮説率と有意に異なる0.05であると言えます。 別の意味では、観測された割合の95%信頼区間は25.6%から61.07%です。 信頼区間は両側検定に対応し、両側検定は、信頼区間に帰無仮説に関連付けられた値が含まれていない場合にのみ拒否されます(この場合は25%)。
計算されたp値が小さい場合、母集団は帰無仮説で最初に述べられたように構造化されていない可能性があります。
計算されたp値が, 低いp値が得られた場合、観察された違いに何らかの効果または理由があるという証拠があります-この場合、投薬。 通常は0.05(または5%)のしきい値が使用され、対応する属性が統計的に有意であるためには、p値がこのしきい値よりも低くなければなりません。
リスク比
確率の別の用語であるリスクは、統計分析のもう一つの基本原則です。 確率は、結果として発生する特定のイベントを観測することと、一意の結果の合計との比較です。, コインフリップは些細な例です:ヘッドを観察するリスクはσまたは50%であり、すべての可能なユニークな試行(ヘッドをもたらすフリップまたはテールをもたらすフリップ)のように、一つだけが関心のあるイベント(ヘッド)です。
リスクのみを使用すると、単一の母集団についての予測が可能になります。 たとえば、米国人口の肥満率を見ると、CDCは、成人の42.4%が2017-2018で肥満であると報告しました。 したがって、肥満である米国の個人のリスクは約42.4%です。 しかし、ほとんどの研究では、特定の介入または他の項目(死亡率など)が別のものに及ぼす影響を調べています。, 以前は、適格な患者の肥満率は25%であると想定していましたが、ここでは米国の成人人口に関連する42.4%を使用します。 薬剤の患者の無作為試料の25%の危険を同様に観察することを仮定して下さい。 肥満に対する薬物の効果を概念化するためには、論理的な次のステップは0.590の危険率で起因する米国の人口の肥満の危険の薬物の米国の人口の肥満の危険を分けることである。,
この計算-二つのリスクの比率は-また、相対リスクとして知られている名を冠したリスク比(RR)統計によって意味されるものです。 することが可能に特定の番号に定が変更された場合、さらにどのくらいのリスク個人を一つのカテゴリー負担に比べて個別の。 この例では、薬を服用している個人は、一般的な米国の人口からの成人と同じくらいのリスクを負います0.59倍。, しかし、我々は、投薬の対象となる人口が25%の肥満率を有していたと仮定している-おそらく、平均して健康である可能性のある若年成人のグループだけが、薬を服用する資格がある。 肥満に対する薬物の効果を調査するとき、これは帰無仮説として使用されるべき割合である。 40%の投薬で肥満率が観察され、有意水準0.05未満のp値が観察された場合、これは投薬が肥満のリスクを増加させるという証拠である(このシナリオではRRは1.6である)。, したがって、関連する統計的予測を行うために帰無仮説を慎重に選択することが重要です。
RRでは、1の結果は両方のグループが同じ量のリスクを有することを示し、1に等しくない結果は、あるグループが別のグループよりも多くのリスクを有することを示し、これは研究によって調べられた介入によるものであると仮定されるリスクである(正式には因果関係の仮定)。
説明するために、我々は脳卒中および脳血管疾患のジャーナルに掲載された2009年の研究の結果を見てください。, この研究では、心電図QTc間隔が延長された患者は、間隔が延長されていない患者と比較して90日以内に死亡する可能性が高いことが報告されている(相対リスク=2.5;95%信頼区間1.5-4.1)。 リスク比に対して1.5と4.1の間の信頼区間を有することは、qtc間隔が延長された患者は、QTc間隔が延長されていない患者よりも1.5-4.1倍90日で死,研究者らは、平均動脈血圧(MAP)>140mmHgまたは<100mmHg(RR=1.8、95%CI1.1-2.9、p=0.027)の患者でRRがほぼ倍に増加することを見出した。 RRに対してCIが1.1-2.9であることは、100-140mmHgの範囲外のMAPを有する患者が、この範囲内の初期MAPを有する患者よりも1.1-2.9倍死亡する可能性,
別の例として、2018年のオーストラリア海軍の新兵に関する研究では、プレハブ装具(足のサポートの一種)を持つものは、少なくとも一つの悪影響を受けるリスクが20.3%であり、ないものは12.4%のリスクがあることが分かった。 ここでのリスク比は0.203/0.124、または1.63で与えられており、足装具を持つ新兵は、いくつかの有害な結果(例えば、足の水疱、痛みなど)を有するリスクの1.63倍を有することを示唆している。)なしのものよりも。 ただし、同じ研究では、リスク比の95%信頼区間が0.96から2.76であり、p値は0.068であると報告されています。, 信頼区間を見ると、95%の報告された範囲(一般的に受け入れられている標準)には、1未満の値、1、および1より上の値が含まれています。 すべての値が母集団統計量である可能性が等しく、95%の信頼度であることを覚えておいて、足装具が効果がない、重大な利益がある、または重大な損 さらに、p値は0.05の標準よりも大きいため、このデータは、水疱や痛みなどの有害事象に一貫した影響を及ぼす足装具の重要な証拠を提供しません。, 前述したように、これは偶然ではありません-それらが同じまたは類似の方法を使用して計算され、p値が両側である場合、信頼区間とp値は同じ結果
正しく利用されると、リスク比は、ある集団が別の集団に負うリスクの変化の母集団における推定を可能にする強力な統計である。, 彼らは理解するのが非常に簡単です(値は、あるグループが別のグループに負うリスクの何倍です)、そして因果関係の方向を仮定して、介入(または他のテストされた変数)が結果に影響を与えるかどうかをすばやく示します。
ただし、制限があります。 第一に、RRsはすべての場合に適用することはできません。 サンプル内のリスクは母集団のリスクの推定値であるため、サンプルは母集団を合理的に代表している必要があります。 したがって、症例対照研究は、結果の比率が制御されているという事実の単純な美徳によって、リスク比を報告することはできない。, 第二に、本明細書で議論されるすべての統計と同様に、RRは相対的な尺度であり、あるグループのリスクに関する情報を他のグループに対して提供する。 ここでの問題は、二つのグループが0.2%と0.1%のリスクを持っていた研究は、2つのグループが90%と45%のリスクを持っていたものと同じRRを負うことです。 どちらの場合も、介入を受けた人が二度のリスクにあったことは事実ですが、これはあるケースでは0.1%のリスクしかなく、別のケースでは45%のリスク, したがって、RRのみを報告することは、第一の例では効果を誇張し、第二の例では潜在的に効果を最小化する(または少なくともそれを非文明化する)。
オッズ比
リスクは試行の総数に関連して関心のあるイベントの数を報告しますが、オッズは関心のないイベントの数に関連して関心のあるイベントの数を報告します。 異なって述べられて、それは非イベントにイベントの数を報告します。, 以前に決定されたように、コインをヘッドに反転させるリスクは1:2または50%ですが、コインをヘッドに反転させるオッズは1:1です(図1)。
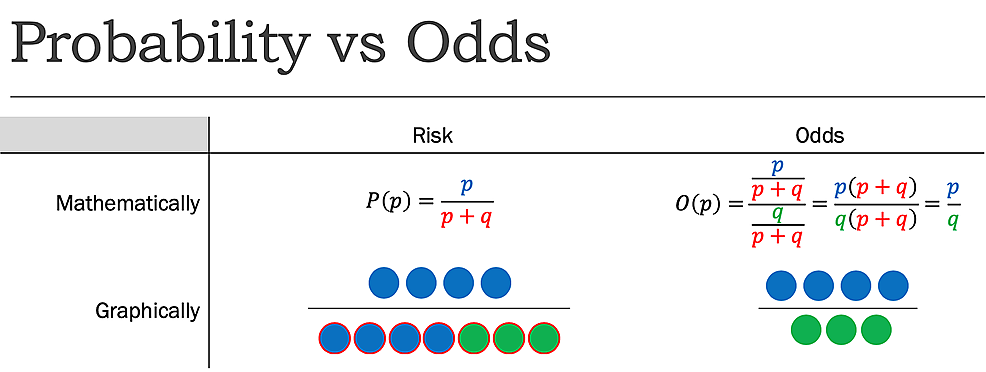
図1:確率(P)対オッズ(O)ここで、p=成功確率とq=失敗の確率
RRと同様に、二つのリスクの比率が二つの別々のグループに対して取られた場合、二つのオッズの比率が二つのグループに対して取られることができる。オッズ比(または)を生成します。, 一方のグループが他方に対してどのくらいのリスクを負うかを報告する代わりに、一方のグループが他方に対してどのくらいのオッズを負うかを報告
ほとんどの場合、これは理解するのがより難しい統計です。 リスクがより直感的な概念頭に、このように理解し相対的にリスクが優先に理解し相対的に…。 しかし、ORはRRと同じ因果関係の仮定の制限に苦しんでおらず、より広く適用できるようになっています。,
例えば、オッズは対称的な尺度であり、リスクは介入を与えられた結果のみを調べるが、オッズは介入を与えられた結果も調べることができる。 したがって、試験グループを選択して結果を測定するのではなく、結果を選択し、他の要因を分析することができる研究を構築することができる。 以下は、ケースコントロール研究の例であり、RRは使用できないが、または使用できない状況である。
2019ケースコントロール研究は良い例を証明しています。, カナダで顕著なa型肝炎ウイルス(HAV)感染といくつかの原因因子との間の潜在的な相関を見つけることを求めて、結果に基づいて研究を構築した(言い換えれば、個人は”介入”、または因果関係が不明であったため、HAVの状態に基づいて分類された)。 この研究では、HAVを患っている人とhavを患っていない人、およびHAV感染前に食べた食べ物を調べました。 このことから、特定の食品とHAVの状態を比較する複数のオッズ比が構築されました。, 例えば、データは、エビ/エビに曝露した被験者のうち、八つはHAVに陽性であったが、七つはなかったが、曝露しなかった被験者のために二つはHAVに陽性であったが、29はなかったことがわかった。 オッズ比は次のように取られます(8:7)/(2:29) これは約16.6に等しい。 研究データは15.75のORを報告し、論文で議論されていない交絡変数の計算前の調整に起因する可能性が高い小さな不一致がありました。 したがって、0.01のp値が報告され、これまたは有意であることの統計的証拠を提供する。,
これは二つの等しい方法で解釈することができます。 第一に、HAVを有する者のエビ/エビ曝露の確率は、そうでない者の場合よりも15.75倍高い。 同等に、HAV-posiitve対HAV-negativeのオッズは、露出していないものよりもエビ/エビにさらされたものの15.75倍高い。
全体的に、または1のスケールで二つの変数間の関連の強さの尺度を提供します関連なしであり、1以上は正の関連であり、1以下は負の関連である。, 前の二つの解釈は正しいですが、それらはRRがあったように直接理解できるものではありませんが、もしそれを決定することが可能であったならば。 別の解釈は、エビ/エビ曝露とHAVとの間に強い正の相関があるということです。
このため、特定の場合には、RRをORで近似することが適切です。 そのような場合、まれな疾患の仮定が成立しなければならない。 つまり、病気は人口の中で非常にまれでなければなりません。, この場合、集団内の疾患のリスク(p/(p+q))は、pがqに対して有意に小さくなるにつれて、集団内の疾患のオッズ(p/q)に近づく。 しかし、この仮定が失敗すると、その差はますます誇張されるようになる。 数学的には、p+q試行では、pを減少させるとqが増加し、同じ合計試行が維持されます。 リスクでは分子のみが変化しますが、オッズでは分子と分母の両方が反対方向に変化します。, その結果、RRおよびORが両方とも1より低い場合、ORはRRを過小評価し、両方が1より上の場合、ORはRRを過大評価します。
RRとしてORを誤って報告すると、しばしばデータを誇張する可能性があります。 ことを覚えておくことが重要であるORはちょうどRRとして相対的な尺度であり、したがって、時には大きなORはオッズ間の小さな差に対応すること
最も忠実な報告については、rrとして提示するか、または提示すべきではなく、まれな疾患仮定が合理的に保持できる場合にのみ、RRの近似値として提示すべきである。, 可能であれば、常にRRを報告する必要があります。
ハザード比
rrとORの両方が介入と結果に関係し、研究期間全体にわたって報告する。 しかし、類似しているが明確な尺度であるハザード比(HR)は、変化率に関係している(表1)。
| RR | または | HR | |
| 目標 | いくつかの変数に基づいてリスクステータスの関係を決定します。 | 二つの変数間の関連付けを決定します。, | かつグループの変化に対す。 |
| 使用する | 介入がリスクをどのように変えるかを教えてくれます。 | 介入とリスクの間に関連があるかどうかを示し、この関連がどのように適用されるかを推定します。 | 介入がイベントを経験する割合をどのように変えるかを教えてくれます。 |
| 制限 | スタディデザインが母集団を代表する場合にのみ適用されます。 ケースコントロール研究では使用できません。 | は一般的にどこにでも適用できますが、必ずしも有用な統計そのものではありません。 リスクを誇張します。, | 一般的に有用であるためには、二つのグループ内の変化率は比較的一貫している必要があります。 |
| タイムライン | 静的-レートを考慮しません。 全体的な研究をまとめたものです。 | 静的-レートを考慮しません。 全体的な研究をまとめたものです。 | レートに基づいています。 研究が時間の経過とともに進行する方法についての情報を提供します。 |
Table1:相対リスク(RR)対オッズ比(OR)対, ハザード比(HR)
HRsは生存曲線と並行しており、そのイベントが死亡であるか病気に罹患しているかにかかわらず、グループ内のあるイベントの時間的進 生存曲線では、縦軸は関心のあるイベントに対応し、横軸は時間に対応します。 イベントのハザードは、グラフの傾き、または時間あたりのイベントに相当します。
ハザード比は、単に二つのハザードの比較です。, 二つの生存曲線が曲線の傾きを比較することによってどれだけ速く発散するかを示すことができます。 1のHRは発散を示しません-両方の曲線内では、イベントの可能性は任意の時点で等しく可能性がありました。 1に等しくないHRは、二つのイベントが等しい速度で発生していないことを示し、あるグループの個人のリスクは、任意の時間間隔で別のグループの個人のリスクとは異なります。
HRsが作る重要な仮定は、比例率の仮定です。, 特異なハザード比を報告するには、二つのハザード率が一定であると仮定する必要があります。 グラフの傾きが変化する場合、比率は同様に時間の経過とともに変化するため、任意の時点での尤度の比較としては適用されません。
特定の癌患者の平均余命を延ばすことを目的とした新規化学療法剤の試験を検討する。 介入群および対照群の両方において、25%が第40週までに死亡していた。, 両方のグループは100%の生存から75%の生存に40週間の期間にわたって減少したので、ハザード率は等しくなり、したがってハザード率は1に等しくなる。 これは、薬物を受け取った個人が、いつでも薬物を受け取っていない人と同じくらい死ぬ可能性があることを示唆しています。
しかし、介入群では、すべての25%が週から10の間に死亡し、対照群では、すべての25%が週から六以内に死亡した可能性があります。 この場合、中央値を比較すると、HRに差がないにもかかわらず、薬物上のものの平均寿命が高くなります。, この場合、ハザード率が時間の経過とともに(非常に劇的に)変化するため、比例ハザードの仮定は失敗します。 このような場合、HRは適用されません。
比例ハザード仮定が合理的に適用されるかどうかを判断することは困難な場合があるため、HRを取ることは時間単位の元の測定値(ハザード率)を取り除くため、時間の中央値と組み合わせてHRを報告することが一般的である。,
Rapid Emergency Medicine Score(REMS)およびWorthing生理学的スコアリングシステム(WPSS)の予後性能を評価する研究では、30日間の死亡率のリスクは、追加のREMSユニットごとに30%増加し(HR:1.28;95%信頼区間(CI):1.23-1.34)、追加のWPSSユニットごとに60%増加した(HR:1.6;95%CI:1.5-1.7)ことが分かった。 この場合、死亡率は変化しなかったが、むしろそれを予測するためのスコアリングシステムが行ったので、HRを使用することができる。 1.5と1の間の信頼区間を持ちます。,WPSSハザード比についての図7は、WPSが高い人の死亡率カーブがより速い速度(約1.5-1.7倍)で低下することを示しています。 間隔の下限はまだ1を超えているので、WPSが高いグループでは30日以内の真の死亡危険性が高いと確信しています。
特定のリスク要因を持つ個人の間でどんちゃん騒ぎ飲酒に関する2018年の研究では、生存曲線は、コントロール、家族歴を持つもの、男性の性別、高衝動性を持つもの、およびアルコールに対するより高い応答を持つもののためのどんちゃん騒ぎ飲酒を達成する率をプロットして構築されました。, 男性および家族歴のある人については、どんちゃん騒ぎを達成する率が高いという統計的に有意な証拠が報告された(男性では1.74、家族歴のある人では1.04のHR)。 しかし、高衝動性を有するもののために、HRは1.17であったが、95%信頼区間は1.00から1.37の範囲であった。 したがって、95%の信頼水準では、HRが1.00であることを除外することは不可能です。,
存在する誇張のために、ORsをRRsとして表すことを避けることが重要であり、同様に、報告されたORは相対的なリスクの良い近似を提供することはめったにないが、むしろ単に相関の尺度を提供することを認識することが重要である。
しっかりした結論と分かりやすさを作る能力のために、rrは可能であれば報告されるべきであるが、その因果関係の仮定に違反した場合(ケースコントロール研究やロジスティック回帰など)、または使用することができる場合には報告されるべきである。,
HRsは生存曲線とともに使用され、ハザード率は時間の経過とともに等しいと仮定されます。 二つのレートを比較するのに便利ですが、比例ハザード仮定を正当化するために、中央値の時間で報告する必要があります。
最後に、HR/RR/または統計量の値にかかわらず、結果が(p値または信頼区間によって決定される)結論に向けて統計的に有意な証拠を提供するかどうかを決定した後にのみ解釈が行われるべきである。, これらの原則とHR/RR/ORの枠組みを覚えておくことは、誤った表現を最小限に抑え、さまざまなサンプルに関する公開された研究の結果から誤った結 図2にまとめた正しいと誤った使い方のこれらの様々なリスクです。
