14.5:パスカルの原理と油圧

パスカルの原理と油圧システムの応用

パスカルの原理を適用することによって、この単純な油圧システムの力の間の関係を導出することができる。 まず、システム内の二つのピストンは同じ高さにあるため、深さの違いによる圧力の違いはありません。 面積A1に作用するF1による圧力は、\(p=\frac{F}{A}\)で定義されるように、単純に

\(p_{1}=\frac{F_{1}}{A_{1}}\)です。,

\

この式は、ピストンが同じ垂直高さにあり、システム内の摩擦が無視できる限り、油圧システムの面積に対する力の比を関連付けます。

油圧システムは、それらに加えられる力を増減することができます。 力をより大きくするために、圧力はより大きな領域に加えられる。 たとえば、図14.16の左円筒に100Nの力が加えられ、右円筒の面積が五倍大きい場合、出力力は500Nになります。, 油圧システムは単純なレバーに似ていますが、一度にいくつかの場所に曲がった曲線を通って圧力を送ることができるという利点があります。

油圧ジャッキはそのような油圧システムです。 油圧ジャッキが自動車を上げるのに自動車整備士によって使用される物のような重負荷を、持ち上げるのに使用されています。 それは各側面の移動可能なピストンによって合うU管の非圧縮性液体から成っている。 Uチューブの一方の側は他方よりも狭い。, 小さな領域に加えられた小さな力は、より大きな領域にわたって反対側のはるかに大きな力のバランスをとることができます（図\(\PageIndex{3}\)）。

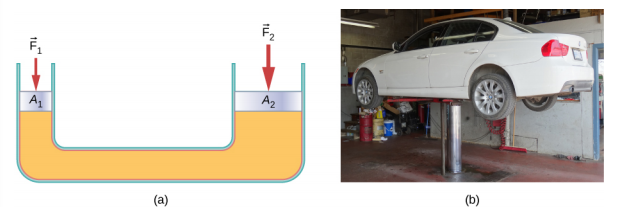
パスカルの原理から、車を持ち上げるのに必要な力は車の重量よりも小さいことが示されます：

\

F1は車を持ち上げるために加えられる力、A1は小さいピストンの断面積、A2は大きいピストンの断面積、F2は車の重量です。