確率
学習目標
*イベント、結果、試行、単純イベント、サンプル空間を定義し、イベントが発生する確率を計算します。
*より複雑な結果のイベントの確率を計算します。
*確率を含むアプリケーションを解きます。
はじめに
確率は、何かが発生する可能性の尺度を提供します。, これは、0と1の間の数字であり、数字を含んでいます。 これは、分数、小数、またはパーセントとして書くことができます。

ランダムに番号を選択すると、それらが選択される特定の順序がないことを意味します。 多くのゲ 確率の計算方法を理解していれば、さまざまな結果の可能性を知ることによって、これらのゲームをプレイする方法について思慮深い決定を下すこ,
定義
まず、確率に関連するいくつかの用語を知る必要があります。 確率で作業する場合、ランダムなアクションまたは一連のアクションは試行と呼ばれます。 結果は試行の結果であり、イベントは特定の結果の集まりです。 イベントは、通常、結果の共通の特性を使用して記述されます。
この言語を適用して、用語が実際にどのように機能するかを見てみましょう。 一部のゲームを必要と転造ダイスと、番号は1から6. (ダイスはダイの複数形です。, 以下の図は、そのようなゲームの試行、結果、およびイベントの使用を示しています。
結果のコレクションは中括弧で囲まれ、カンマで区切られていることに注意してください。
単純なイベントは、一つだけの結果を持つイベントです。 1を転がすことは、単純なイベントになります。1つだけの結果があるので、それは簡単です。 イベントには有効な結果として6のみが含まれているため、5を超えるローリングも単純なイベントになります。 複合イベントは、複数の結果を持つイベントです。 たとえば、六面ダイをローリングする場合、偶数をローリングすると、2、4、6のいずれかの結果が発生する可能性があります。,
あなたが六面ダイを何度も転がすとき、あなたはどんな結果も他のものよりも頻繁に起こることを期待すべきではありません(それが公正なダイ このような状況での結果は、同様に可能性が高いと言われています。 確率を計算するときに、結果がいつ同じ可能性があるかを認識することは非常に重要です。 ダイローリングトライアルの各結果は同様に可能性が高いため、ロールの各結果![]() を取得することが期待されます。, つまり、ロールの
を取得することが期待されます。, つまり、ロールの![]() が1、ロールの
が1、ロールの![]() が2、ロールの
が2、ロールの![]() が3などになります。
が3などになります。
スピナーは四つの等しい部分に分かれており、それぞれ異なる色で着色されています。 このスピナーがスピンされると、矢印は色のいずれかを指します。 結果は同じように可能性がありますか?
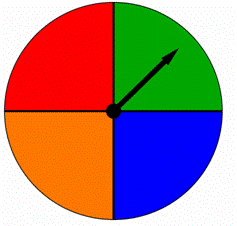
A)はい、それらは同様に可能性があります。
B)いいえ、それらは同じように可能性が高いわけではありません。,
イベントの確率
イベントの確率は、発生すると予想される頻度です。 これは、サンプル空間のサイズに対するイベント空間のサイズの比率です。
まず、サンプル空間のサイズを決定する必要があります。 標本空間のサイズは、考えられる結果の総数です。 たとえば、1つのダイをロールすると、サンプルスペースは1, 2, 3, 4, 5, または6. したがって、サンプル空間のサイズは6です。
次に、イベントスペースのサイズを決定する必要があります。, イベントスペースは、あなたが興味を持っているイベントの結果の数です。 三つ未満の数を転がすためのイベントスペースは、1または2です。 だから、イベントスペースのサイズは2です。
同様に可能性の高い結果については、イベントEの確率はP(E)と書くことができます。
![]()
|
例 |
||
|
problem |
ゲームには、1から6までの番号の六面ダイをローリングする必要があります。, 偶数を転がす確率はどれくらいですか? |
|
|
サンプルスペース= {1, 2, 3, 4, 5, 6}
イベントスペース= {2, 4, 6} |
まず、サンプルスペースとイベントスペースを見つけます。 サンプルスペースはすべての可能な結果であり、イベントスペースはイベントの結果です。 この場合、イベントは”偶数のローリング”です。,” |
|
|
|
結果は同様に可能性が高いため、イベントの確率はサンプル空間に対するイベント空間の比率です。, |
|
|
回答 |
P(偶数)= |
|
確率を最も低い項に単純化することは、一般的な分数と同様に、確率を持つ一般的な方法です。 そうしない理由がない限り、すべての最終確率を最低の条件で表現します。,
スピナーは、以下に示すように、それぞれ異なる色で着色された等しい部分に分割されています。, このスピナーで青または緑を回転させる確率を求めます。
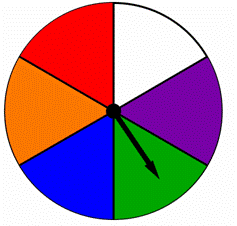
A)![]()
B)![]()
C)2
D)6
サンプルスペースを見つけるためのカウント方法
確率を計算するための最も困難なことは、二つ以上の試行がある場合は特に、サンプルスペースのサイズを見つけることができます。 助けることができる複数のカウント方法がある。,
最初に見るのはチャートを作成することです。 以下の例では、トリは二つのコインを反転させています。 そのため、サンプル空間を慎重に決定する必要があります。 次の例に示すようなチャートは良いアプローチです。
|
例 |
||||
|
問題 |
トリはコインのペアを反転し、彼女が取得する”頭”のどのように多くのフリップに注意しています。 彼女が2つの頭を反転させる確率は何ですか?, 彼女が1頭だけ反転する確率はどれくらいですか?,15ecf6″>T |
T |
TT |
|
sample space: {HH, HT, TH, TT}
event space for 2 heads: {HH}
event space for 1 head: {HT, TH}
Create a chart to record the results of flipping the first coin, followed by the result of flipping the second coin.,
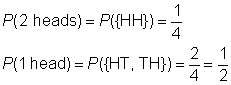
結果は同様に可能性が高いため、イベントの確率はサンプル空間に対するイベント空間の比率です。,
回答
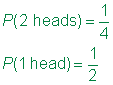
以下の例では、toriのサンプルスペースは一つのダイのみがロールされているので単純です。 しかし、ジェームスは二つの金型では、図表を整理します。,
|
例 |
||||||||
|
問題 |
トーリは六面のダイを巻き、1または4のいずれかの結果を得たかった。 ジェームズは青と赤の二つの六面のサイコロを転がし、同時に1と3の両方の結果を得たかった。 どのイベントの確率が高いですか?, | |||||||
|
Tori’s sample space: {1, 2, 3, 4, 5, 6}
Tori’s event space: {1, 4}
Tori:
|
First, find the sample space and the event space for the two trials., トーリの裁判にとって、これは簡単です。 結果は等しく可能性が高いので、事象の確率は標本空間に対する事象空間の比率である。,316594724″> 6 |
6,1 |
6,2 |
6,3 |
6,4 |
6,5 |
6,6 |
|
James’ sample space has 36 outcomes.,
ジェームズのイベントスペースには2つの結果があります。
彼は二つのサイコロを転がしているので、ジェームズの裁判のためにそれほど明白ではありません。 可能性を見つけるのに図表を使用しなさい。
36の結果があります。 これらのうち、2つがあり、1と3の両方を持っています。,
ジェームズ:![]()
結果は同様に可能性が高いため、イベントの確率はサンプル空間に対するイベント空間の比率です。
回答
トーリのイベントはより大きな確率を持ちます。,
サンプル空間を決定するためにツリーダイアグラムを使用することもできます。 ツリー図には、各イベントの可能なすべての結果に対する分岐があります。
クローゼットには、三対のズボン(黒、白、緑)、四つのシャツ(緑、白、紫、黄色)、二対の靴(黒と白)があるとします。 どのように多くの異なる衣装を作ることがで ズボンのための3つの選択、ワイシャツのための4つの選択、および靴のための2つの選択が, ツリー図では、黒にはB、白にはW、緑にはG、紫にはP、黄色にはYを使用しましょう。
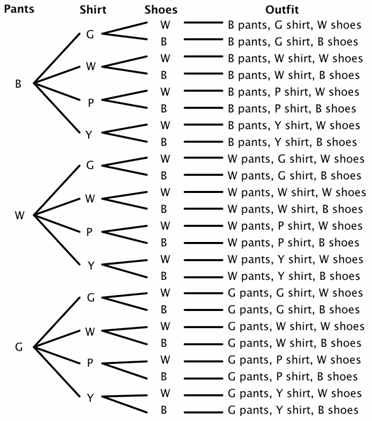
ツリー図から、サンプル空間に24の可能な衣装(おそらく素晴らしい選択肢ではない)があることがわかります。
これで、いくつかの確率問題をかなり簡単に解決できます。 たとえば、目を閉じてランダムに選択すると、同じ色のパンツと靴を選択する確率はどれくらいですか? あなたはズボンと靴が一致する8つの衣装があることがわかります。,
![]()
ご覧のように、試行に複数のコインを反転させたり、複数のダイを転がしたりするなど、複数のランダム要素が含まれる場合、確率を計算するためにサンプル空間のすべての結果を特定する必要はありません。 あなただけの結果の数が必要です。
基本的なカウント原則は、それらの一つ一つをリストしてカウントせずに結果の数を見つける方法です。,
基本的なカウント原則
あるイベントにpの可能な結果があり、別のイベントにmの可能な結果がある場合、二つのイベントについてp•mの可能な結果の合計があります。
例
*ローリング二つの六面サイコロ:各ダイは6等しく可能性の高い結果を持っているので、サンプルスペースは6•6または36等しく可
*三つのコインを反転:各コインは2等しく可能性の高い結果を持っているので、サンプルスペースは次のようになります2 • 2 • 2 または8等しく可能性の高い結果。,
•六面ダイを転がし、コインを反転:サンプルスペースは6*2または12等しく可能性の高い結果です。
だから、あなたは基本的なカウント原則を使用して、前の例にあるどのように多くの衣装を見つけることができます。 ズボンのための3つの選択、ワイシャツのための4つの選択、および靴のための2つの選択が 使の基本的な計数原則としてい4 • 3 • 2 =24違います。,
|
例 |
||
|
問題 |
バリーは他のすべてのボランティアのための昼食を作る慈善の歩行でボランティア。 各バッグには、 ·二つのサンドイッチ(ピーナッツバターとゼリー、または七面鳥とチーズ)の一つ、 ·三つのチップ(通常のポテトチップス、ベイクドポテトチップス、またはコーンチップス)の一つ、 ·果物の一つ(リンゴまたはオレンジ)。, 彼は袋に入っていたものをマークするのを忘れてしまった。 それぞれの選択肢が均等に可能性が高いと仮定すると、テレーズがピーナッツバターとゼリーサンドイッチとリンゴを保持する袋が得られる確率は何です, |
|
|
Size of sample space:
(number of sandwich choices) • (number of chip choices) • (number of fruit choices) = 2 • 3 • 2 = 12
|
First, use the Fundamental Counting Principle to find the size of the sample space., |
|
|
イベントスペースのサイズ:
(サンドイッチの選択肢の数イベント)•(イベント内のチップの選択肢の数)•(イベント内のフルーツの選択肢の数)= |
イベントスペースについては、同じ原則に従います。 この場合、そこに唯一のサンドイッチと関心のある果物の一枚がありますが、チップの三種類のいずれかが許容されます。, |
|
|
回答 |
|
比率を使用して確率を求めます。 |
キャリーは四つのコインを反転し、尾の数をカウントします。 HHHT、HHTH、HTHH、およびTHHH:正確に一つの尾を取得する四つの方法があります。 キャリーが正確に一つの尾を得る確率はどれくらいですか?,
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Summary
Probability helps you understand random, unpredictable situations where multiple outcomes are possible., それはイベントの可能性の尺度であり、それらの結果がすべて等しく可能性がある場合、イベントと可能な結果の比率に依存します。