公開鍵暗号
対称鍵暗号とは異なり、公開鍵暗号の歴史的な使用は見つかりません。 それは比較的新しい概念です。
対称暗号は、機密通信に関与している政府、軍隊、大手金融企業などの組織に適していました。,
過去数十年間でより安全でないコンピュータネットワークの普及に伴い、より大規模な暗号化を使用する真の必要性が感じられました。 対称鍵は、鍵管理のために直面した課題のために実用的ではないことが判明しました。 これは公開鍵暗号システムを生じさせた。
暗号化と復号化のプロセスを次の図に示します−
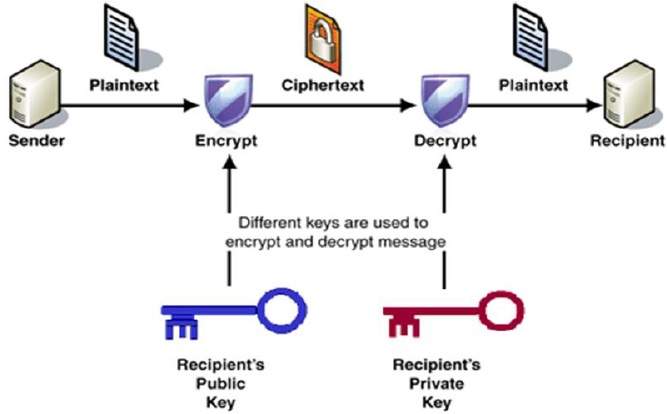
公開鍵暗号化方式の最も重要なプロパティは次のとおりです-
-
暗号化と復号化には異なるキーが使用されます。, これは、対称暗号化方式とは異なるこの方式を設定するプロパティです。各受信者は、一般に自分の秘密鍵と呼ばれる一意の復号鍵を有する。
-
受信者は、自分の公開鍵と呼ばれる暗号化キーを公開する必要があります。
-
この方式では、受信者としての敵によるなりすましを避けるために、公開鍵の真正性の保証が必要である。 一般に、このタイプの暗号システムには、特定の公開鍵が特定の個人またはエンティティのみに属していることを証明する信頼できる第三者が含,
-
暗号化アルゴリズムは、攻撃者が暗号文および暗号化(公開)鍵から平文を推測することを禁止するのに十分複雑です。
-
秘密鍵と公開鍵は数学的に関連しているが、公開鍵から秘密鍵を計算することは不可能である。 実際、公開鍵暗号システムのインテリジェントな部分は、二つの鍵間の関係を設計することにあります。
公開鍵暗号化方式には三つのタイプがあります。, 次のセクションでそれらについて説明します−
RSA暗号システム
この暗号システムは初期システムの一つです。 それは今日でも最も採用された暗号システムのままです。 このシステムはRon Rivest、Adi Shamir、Len Adlemanの三人の学者によって発明されたため、RSA暗号システムと呼ばれています。
RSA暗号システムの二つの側面、第一に鍵ペアの生成と第二に暗号化-復号化アルゴリズムについて説明します。,
RSAキーペアの生成
暗号化を使用した通信に参加したい個人または当事者は、公開鍵と秘密鍵のペアを生成する必要があります。 鍵の生成に続くプロセスは以下で説明されます−
-
RSAモジュラス(n)を生成します
-
二つの大きな素数、pとqを選択します。
-
n=p*qを計算します。強力なアンブレイカブル暗号化の場合、nを大きな数、通常は最小512ビットとします。,
-
-
派生数(e)を見つける
-
数eは1より大きく、(p−1)(q−1)より小さくなければなりません。
-
eと(p−1)(q−1)には、1を除いて共通の因子はあってはなりません。 言い換えれば、二つの数eと(p–1)(q–1)は互いに素である。
-
-
公開鍵を形成する
-
数字のペア(n、e)がRSA公開鍵を形成し、公開されます。,
-
興味深いことに、nは公開鍵の一部ですが、大きな素数を因数分解することが困難であるため、攻撃者はnを得るために使用される二つの素数(p&q)を有限時間で見つけることができないことが保証されます。p>
-
-
秘密鍵を生成する
-
秘密鍵dは、p、q、およびeから計算されます。nとeに対して、一意の数値dがあります。
-
数値dは、e modulo(p-1)(q–1)の逆数です。, これは、dが(p-1)(q-1)より小さい数であり、eを掛けたときに1modulo(p-1)(q-1)に等しいことを意味します。
-
この関係は数学的に次のように書かれます−
-
ed = 1 mod (p − 1)(q − 1)
拡張ユークリッドアルゴリズムは、p、q、eを入力として受け取り、dを出力として与えます。
例
RSAキーペアを生成する例を以下に示します。 (理解を容易にするために、ここで取られた素数p&qは小さな値です。 実際には、これらの値は非常に高い)。,
-
二つの素数をp=7かつq=13とする。 したがって、モジュラスn=pq=7×13=91である。
-
E=5を選択しますが、これは5と(p−1)(q)の共通因子である数がないため有効な選択です− 1) = 6 × 12 = 72, 1を除く。
-
数字のペア(n,e)=(91,5)が公開鍵を形成し、暗号化されたメッセージを送信できるようにしたい人は誰でも利用可能にすることができます。
-
拡張ユークリッドアルゴリズムにp=7、q=13、およびe=5を入力します。 出力はd=29になります。,
-
計算されたdが正しいことを確認してください−
de = 29 × 5 = 145 = 1 mod 72
-
したがって、公開鍵は(91,5)、秘密鍵は(91,29)です。
暗号化および復号化
鍵ペアが生成されると、暗号化および復号化のプロセスは比較的簡単で計算が容易である。
興味深いことに、RSAは対称鍵暗号化の場合のようにビット列に対して直接動作しません。 したがって、平文をnより小さい一連の数として表す必要があります。,
RSA暗号化
-
送信者が公開鍵が(n,e)であるユーザーにテキストメッセージを送信したいとします。暗号化プロセスは、単純な数学的ステップです−
C = Pe mod n
-
言い換えれば、暗号文Cは、平文Pが乗算されたものと等しくなります。
-
暗号文Cは、平文Pが乗算されたものと等しくなります。
-
平文P=10での鍵生成の例に戻ると、暗号文C−
暗号文Cは、平文Pが乗算されたものと等しくなります。
これは、Cもnより小さい数であることを意味します。,
C = 105 mod 91
RSA復号化
-
RSAの復号化プロセスも非常に簡単です。 公開鍵ペア(n,e)の受信者が暗号文Cを受信したとします。
-
受信者はcを秘密鍵dの累乗に上げます。nを法とする結果は平文Pになります。,
Plaintext = Cd mod n
-
数値例に戻ると、暗号文C=82は秘密鍵を使用して番号10に復号化されます29−
Plaintext = 8229 mod 91 = 10
RSA Analysis
RSAのセキュリティは、二つの別々の関数の強さに依存します。 RSA暗号システムは、非常に大きな数を因数分解する実用的な難しさに基づいている最も人気のある公開鍵暗号システムの強さです。,
-
暗号化機能−平文を暗号文に変換する一方向関数とみなされ、秘密鍵dの知識でのみ逆にすることができます。
-
鍵生成-RSA公開鍵から秘密鍵を決定することの難しさは、モジュラスnを因数分解することと同等です。したがって、攻撃者はNを因数分解できない限り、RSA公開鍵の知識を使用してRSA秘密鍵を決定することはできません。pモジュラスnへのQ値は簡単ですが、逆は不可能です。,
これら二つの関数のいずれかが一方向でないことが証明された場合、RSAは壊れます。 実際、効率的に因数分解するための技術が開発されれば、RSAはもはや安全ではなくなります。数pとqが大きな素数でない場合、および/または選択された公開鍵eが小さい場合、RSA暗号化の強度は攻撃に対して大幅に低下します。
ElGamal暗号システム
RSAとともに、他の公開鍵暗号システムが提案されています。 それらの多くは、離散対数問題の異なるバージョンに基づいています。,
楕円曲線バリアントと呼ばれるElGamal暗号システムは、離散対数問題に基づいています。 これは、離散対数が与えられた数の実用的な時間枠では見つからないという仮定から強さを導き、べき乗の逆演算を効率的に計算できるという仮定から強さを導出する。
私たちはpを法とする数で動作ElGamalの簡単なバージョンを見てみましょう。楕円曲線のバリアントの場合、それは全く異なる数体系に基づいています。,
ElGamal鍵ペアの生成
ElGamal暗号システムの各ユーザは、次のようにして鍵ペアを生成します。
-
大きな素数pを選択します。一般に、1024−2048ビット長の素数が選択されます。
-
ジェネレータ要素gを選択します。
-
この数は1からp−1の間でなければなりませんが、任意の数にすることはできません。
-
これは、pを法とする整数の乗法群の生成元であり、すべての整数mに対して、gk=mod nであるような整数kが存在することを意味する。,
たとえば、3はグループ5(Z5)の生成元です= {1, 2, 3, 4}).
-
| N | 3n | 3n mod5 |
|---|---|---|
| 1 | 3 | 3 |
| 2 | 9 | 4 |
| 3 | 27 | 2 |
| 4 | 81 | 1 |
-
秘密鍵を選択します。 秘密鍵xは、1より大きく、p−1より小さい任意の数値です。
-
公開キーの一部を計算します。, 値yは、パラメータp、g、および秘密鍵xから次のように計算されます−
y = gx mod p
-
公開鍵を取得します。 ElGamal公開鍵は、三つのパラメータ(p、g、y)からなります。
例えば、p=17かつg=6と仮定する(6は群Z17の生成元であることが確認できる)。 秘密鍵xは、1より大きく71より小さい任意の数にすることができるので、x=5を選択します。 値yは次のように計算されます−
y = 65 mod 17 = 7
-
したがって、秘密鍵は62であり、公開鍵は(17、6、7)です。,
暗号化および復号化
ElGamalキーペアの生成は、RSAの同等のプロセスよりも比較的簡単です。 しかし、暗号化と復号化はRSAよりもわずかに複雑です。
ElGamal Encryption
送信者がElGamal公開鍵が(p,g,y)である誰かに平文を送信したいと仮定し、−
-
送信者は平文をpを法とする一連の数値として表します。
-
最初の平文Pを暗号化し、pを法とする数値として表されます。, 暗号文Cを取得するための暗号化プロセスは、次のようになります−
- ランダムに番号kを生成します;
- 二つの値C1とC2を計算します。−
C1 = gk mod pC2 = (P*yk) mod p
-
二つの別々の値(C1、C2)からなる暗号文Cを一緒に送信します。,
-
上記のElGamal鍵生成の例を参照すると、平文P=13は次のように暗号化されます−
- ランダムに数を生成し、k=10
- 二つの値C1とC2を計算します。
C1 = 610 mod 17C2 = (13*710) mod 17 = 9
-
暗号文C=(C1,c2)=(15,9).,
ElGamal Decryption
-
秘密鍵xを使用して暗号文(C1,C2)を復号化するには、次の二つのステップが実行されます−
-
一般に復号係数と呼ばれる(C1)-x,
-
次の式を使用して平文を取得します−
-
C2 × (C1)-x mod p = Plaintext
-
この例では、暗号文C=(C1,C2)=(15,9)を秘密鍵x=5を使用して復号化するために、復号係数は
15-5 mod 17 = 9
-
平文p=(9×9)mod17=13を抽出します。
ElGamal Analysis
ElGamalシステムでは、各ユーザーは秘密鍵xを持っています。, ElGamalの強さは離散対数問題の難しさに基づいています。
セキュアキーサイズは一般的に>1024ビットです。 今日でも2048ビットの長いキーが使用されています。 処理速度の面では、Elgamalはかなり遅く、主に鍵認証プロトコルに使用されます。 より高い処理効率が原因で、ElGamalの楕円曲線の変形はますます普及するようになっている。,
楕円曲線暗号(ECC)
楕円曲線暗号(ECC)は、セキュリティが離散対数問題の特別なバージョンに基づいている暗号化ツールとプロトコルのスイートを表すために使用される用語です。 ECCは、楕円曲線と呼ばれる数学的オブジェクトに関連付けられている数のセットに基づいています。
ECCは、楕円曲線と呼ばれる数学的対象に関連付 Pを法とする数の場合と同じように、これらの数の倍数を追加して計算するための規則があります。,
ECCには、ElGamal暗号化やデジタル署名アルゴリズムなどのモジュラー番号のために最初に設計された多くの暗号方式の変種が含まれています。
離散対数問題は、楕円曲線上の点に適用するとはるかに困難であると考えられています。 これにより、pを法とする数から楕円曲線上の点への切り替えが促されます。 また同等のセキュリティレベルを達成することができます。短キーを使用した場合は楕円曲線に基づく変更されることもあります。,
短い鍵は二つの利点をもたらします−
- 鍵管理の容易さ
- 効率的な計算
これらの利点は、計算リソースが制約されているアプリケーションにとって、楕円曲線ベースの暗号化方式
RSAおよびElGamalスキーム–比較
さまざまな側面についてRSAおよびElGamalスキームを簡単に比較しましょう。
| RSA | ElGamal |
|---|---|
| 暗号化の方が効率的です。 | これは、復号化のために、より効率的です。, |
| これは、復号化のためにあまり効率的ではありません。 | これは、復号化のために、より効率的です。 |
| 特定のセキュリティレベルでは、RSAでは長いキーが必要です。 | 同じレベルのセキュリティのためには、非常に短いキーが必要です。 |
| それは広く受け入れられ、使用されています。td> | それは新しく、市場ではあまり人気がありません。 |