相関的研究:変数間の関係を求める
主に静的な画像を提供するために設計された記述的研究とは対照的に、相関的研究は、二つ以上の関連変数の測定と、それらの変数間または変数間の関係の評価を含みます。, たとえば、身長と体重の変数は、背の高い人が一般的に短い人よりも体重が多いため、体系的に関連しています(相関しています)。 同じように、人が単語のリストを研究するために与えられる時間が多いほど、彼または彼女が作るエラーが少なくなるので、研究時間と記憶エラーも関連 研究デザインに二つの変数がある場合、そのうちの一つは予測子変数と呼ばれ、もう一つは結果変数と呼ばれます。, ここで、湾曲した矢印は二つの変数間の予想される相関を表します。
図2.2.2

相関研究からのデータを整理する一つの方法二つの変数では、散布図を使用して測定された変数のそれぞれの値をグラフ化することです。 図2.10″散布図の例”でわかるように、散布図は二つの変数間の関係を視覚的にイメージしたものです。, ポイントは、二つの変数のための彼または彼女のスコアの交差点で各個人のためにプロットされます。 図2.10″散布図の例”の(a)と(b)の部分のように、散布図上の変数間の関連を直線で簡単に近似できる場合、変数は線形関係を持つと言われています。
直線が、ある変数について平均以上の値を持つ個人も、一部(a)のように、他の変数について平均以上の値を持つ傾向があることを示す場合、その関係は正の線形であると言われます。, 正の線形関係の例には、身長と体重の間、教育と収入の間、および子供の年齢と数学的能力の間などがあります。 いずれの場合も、一方の変数で高いスコアを獲得する人は、他方の変数で高いスコアを獲得する傾向があります。 対照的に、一部(b)に示すように、負の線形関係は、ある変数の平均を上回る値が他の変数の平均を下回る値と関連付けられる傾向がある場合に生じる。, 負の線形関係の例には、子供の年齢と子供が使用するおむつの数との間、および学習タスクで行われた練習とエラーとの間のものが含まれる。 これらのケースでは、変数のいずれかで高いスコア人は、他の変数に低いスコアする傾向があります。
直線で記述できない変数間の関係は、非線形関係として知られています。 図2.10″散布図の例”のパート(c)は、点の分布が本質的にランダムである一般的なパターンを示しています。, この場合、二つの変数の間には全く関係がなく、それらは独立であると言われています。 図2.10″散布図の例”の(d)と(e)の部分は、関連があるが、点が単一の直線ではうまく記述されていない関連のパターンを示している。 例えば、パート(d)は、不安とパフォーマンスの間に頻繁に発生する関係のタイプを示しています。, 低レベルから中レベルへの不安の増加は、パフォーマンスの増加と関連しているが、中レベルから高レベルへの不安の増加は、パフォーマンスの低下と 方向が変わり、したがって単一の直線によって記述されない関係は曲線関係と呼ばれます。
図2.10散布図の例
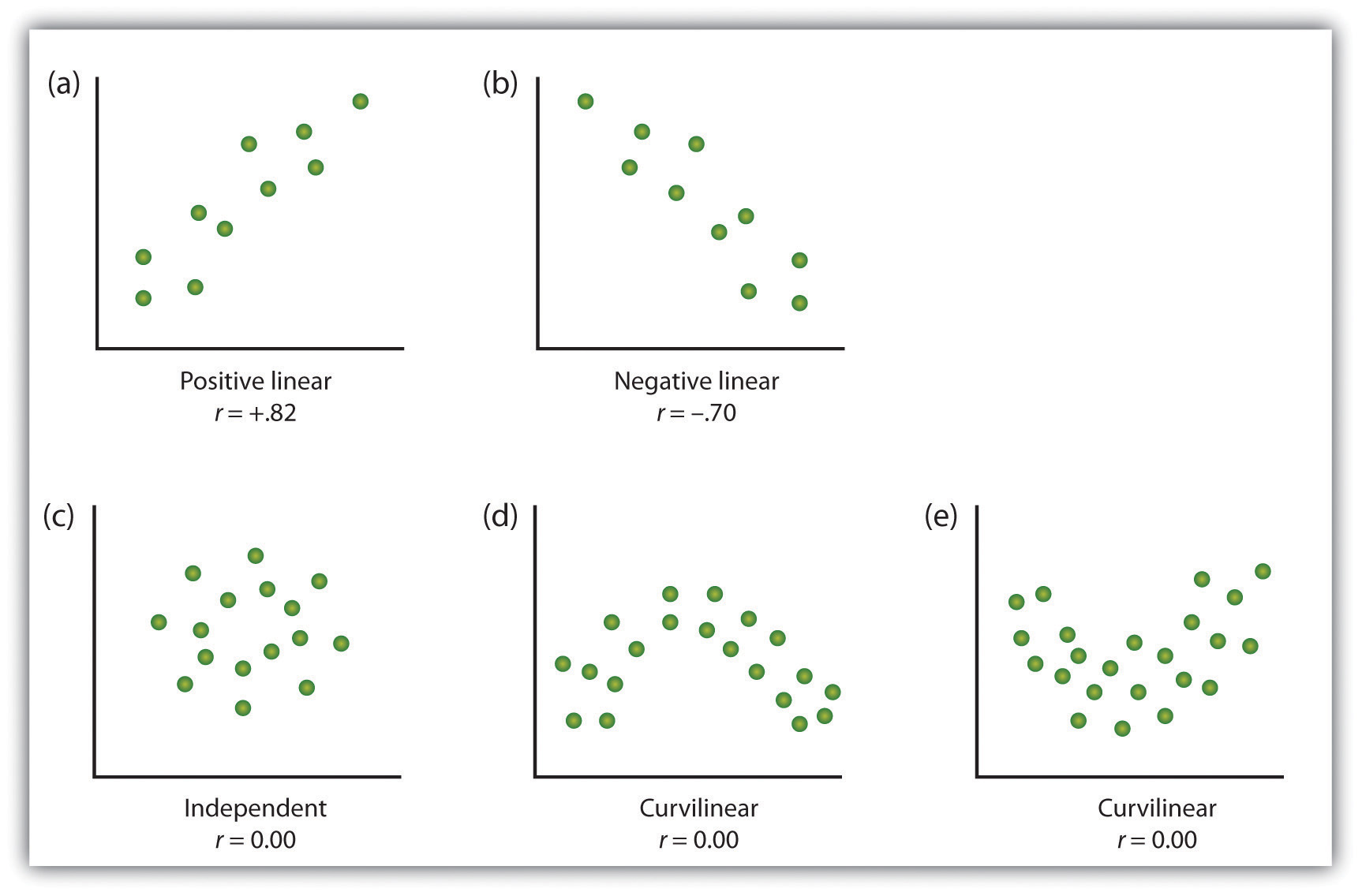
散布図に示すように、二つの変数間の関係の例をいくつか示します。, 曲線的な関係を持つ変数間のピアソン相関係数(r)は、おそらくゼロに近くなることに注意してください。
Stangor、C.(2011)から適応されています。 行動科学のための研究方法(第4編。). マウンテンビュー、CA:Cengage。
変数間の線形関係の強さの最も一般的な統計的尺度は、文字rで象徴されるピアソン相関係数です。相関係数の値は、r=-1.00からr=+1.00の範囲です。, 線形関係の方向は、相関係数の符号によって示される。 Rの正の値(r=など。54またはr=。67)は、関係が正の線形であることを示します(つまり、散布図上の点のパターンは左下から右上に向かって実行されます)が、rの負の値(r=–など)です。30またはr=-。72)負の線形関係を示します(すなわち、ドットは左上から右下に実行されます)。 線形関係の強さは、相関係数のゼロからの距離(その絶対値)によって索引付けされます。, たとえば、r=–です。54はr=よりも強い関係です。30、およびr=。72はr=–よりも強い関係です。57. ピアソン相関係数は線形関係のみを測定するため、曲線関係を持つ変数はrでは十分に記述されず、観測された相関はゼロに近くなります。
同時に二つ以上の測度間の関係を調べることも可能です。, 単一の結果変数を予測するために複数の予測子変数を使用する研究デザインは、重回帰によって分析されます(Aiken&West、1991)。 重回帰は、複数の予測子変数から単一の結果変数を予測することを可能にする変数間の相関係数に基づく統計的手法です。 たとえば、図2.11″三つの予測子変数からのジョブパフォーマンスの予測”は、三つの予測子変数を使用して単一の結果を予測する重回帰分析を示してい, 重回帰分析の使用は、相関研究デザインの重要な利点を示しています—それらは、他の変数の知識に基づいて、結果変数(例えば、仕事のパフォーマンス)に関する人の可能性の高いスコアについて予測を行うために使用することができます。
図2.11三つの予測子変数からのジョブパフォーマンスの予測
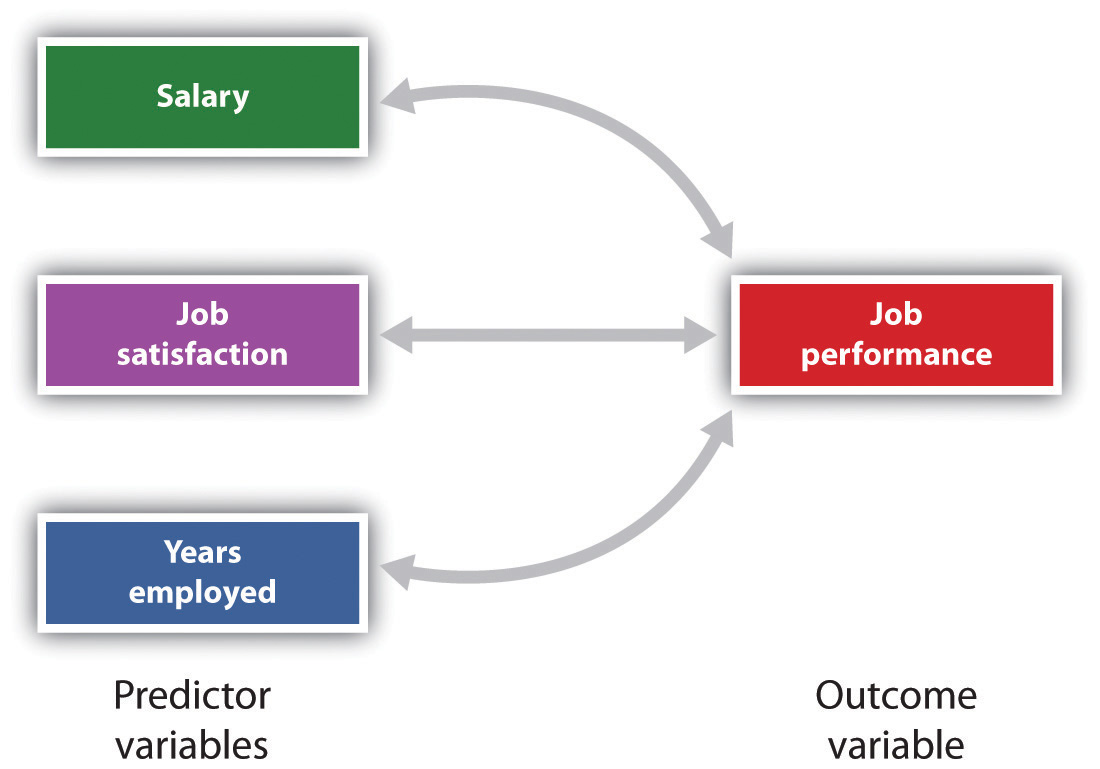
重回帰により、科学者は複数の予測子変数を使用して単一の結果変数のスコアを予測することができます。,
相関研究デザインの重要な制限は、測定された変数間の因果関係についての結論を引き出すためにそれらを使用できないことです。 例えば、暴力的な行動を見ると子供の積極的な遊びが増えると仮定した研究者を考えてみましょう。 彼は、四年生の子供たちのサンプルから、週の間に各子供のビューを示しているどのように多くの暴力的なテレビの尺度だけでなく、各子供が学校の遊び場でどのように積極的に果たしているかの尺度を収集しています。, 彼の収集されたデータから、研究者は二つの測定された変数間の正の相関を発見する。
この正の相関は研究者の仮説を支持するように見えるが、暴力的なテレビを見ることが攻撃的な行動を引き起こすことを示すことはできない。 研究者は、暴力的なテレビを見ることは積極的な遊びを引き起こすと仮定するように誘惑されていますが、
図2.2.2

他の可能性があります。, 別の可能性の一つは、因果関係の方向が仮説されているものとはまったく反対であるということです。 おそらく、学校で積極的に行動した子供たちは、自宅で暴力的なテレビ番組を見たいと思う残留興奮を発症します。
図2.2.2

この可能性は低いように見えるかもしれませんが、
この可能性は低いかもしれませんが、
この可能性は低いかもしれませんが、
、この観察された相関に基づいて、このような逆の因果関係の可能性を排除する方法はない。,
図2.2.2

観測された相関についてさらに別の可能な説明は、それが生成されたことである。共通因果変数(また、第三変数として知られている)の存在によって。, 共通因果変数は、研究仮説の一部ではないが、予測変数と結果変数の両方を引き起こし、それらの間に観測された相関を生成する変数である。 この例では、潜在的な共通因果変数は、子供の両親の規律スタイルです。 厳しい懲罰的な規律スタイルを使用する親は、暴力的なテレビを見るのが好きで、両親があまり厳しい規律を使用していない子供と比較して積極的に振る舞う子供を生み出す可能性があります。
図2.2。,2
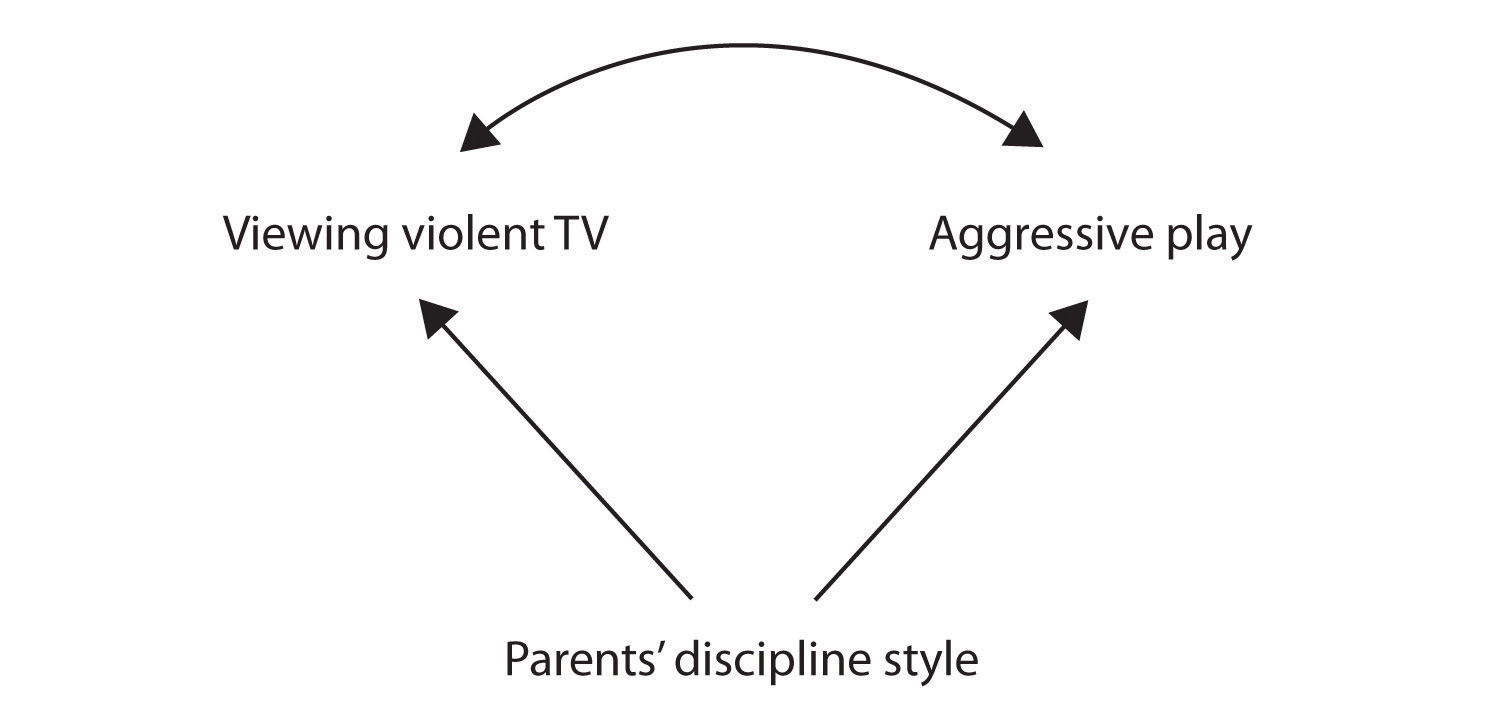
この場合、テレビの視聴と積極的なプレイは正の相関があります(それらの間の湾曲した矢印によって示されるように)、どちらも一方が他方を引き起こしたが、どちらも親の規律スタイル(まっすぐな矢印)によって引き起こされたにもかかわらず、両方とも両親の規律スタイル(真っ直ぐな矢印)によって引き起こされたにもかかわらず。 予測変数と結果変数の両方が共通因果変数によって引き起こされる場合、それらの間の観測された関係は偽であると言われます。, 偽の関係は、共通因果変数が関係を生成し、”離れて説明”する二つの変数間の関係です。 共通因果変数の効果が取り除かれたり、制御されたりすると、予測変数と結果変数の関係は消えます。 この例では、両親の規律スタイルの影響を制御することによって、テレビ視聴と攻撃的な行動との関係がなくなる可能性があるため、侵略とテレビ,
相関研究デザインにおける共通因果変数は、測定されていないため、その存在とアイデンティティは通常研究者には不明であるため、”謎”変数と考えることができる。 予測変数と結果変数の両方を引き起こす可能性のあるすべての変数を測定することは不可能であるため、未知の共通因果変数の存在は常に可能 このため、相関研究の基本的な制限が残されています:相関は因果関係を示していません。, 相関研究プロジェクトについて読むときは、偽の関係の可能性を念頭に置き、その結果を適切に解釈してくださいことが重要です。 相関研究は、逆の因果関係や共通の因果関係の変数の可能性について言及することなく因果関係を示すと報告されることがありますが、あなたのよ
要するに、相関研究デザインには強みと限界の両方があります。, 一つの強みは、予測子変数を操作することができないため、実験的な研究が不可能な場合に使用できるということです。 相関デザインはまた、研究者が日常生活の中で起こる行動を研究できるようにするという利点もあります。 また、相関デザインを使用して予測を行うこともできます—例えば、テストのバッテリーのスコアから、トレーニングセッション中の職業訓練生の成功を予 が使えないなど相関情報かどうか判断するための研修によりよい。 そのために、研究者は実験に頼っています。,