valószínűség
tanulási cél(ok)
· Esemény, eredmény, próba, Egyszerű esemény, mintaterület meghatározása és az esemény bekövetkezésének valószínűségének kiszámítása.
· Számítsa ki az események valószínűségét összetettebb kimenetelek esetén.
· valószínűségeket érintő alkalmazások megoldása.
Bevezetés
a valószínűség megmutatja, mennyire valószínű, hogy valami bekövetkezik., Ez egy szám a 0 és az 1 számok között és között. Meg lehet írni, mint egy frakció, decimális, vagy egy százalék.

a számok véletlenszerű kiválasztása azt jelenti, hogy nincs konkrét sorrend, amelyben kiválasztják őket. Sok játék kocka vagy spinners segítségével véletlenszerűen generál számokat. Ha megérti, hogyan kell kiszámítani a valószínűségeket, átgondolt döntéseket hozhat arról, hogyan kell játszani ezeket a játékokat a különböző eredmények valószínűségének ismeretében.,
definíciók
először ismernie kell a valószínűséggel kapcsolatos néhány kifejezést. Ha valószínűséggel dolgozik, egy véletlenszerű műveletet vagy műveletsorozatot próbának neveznek. Az eredmény egy tárgyalás eredménye, az esemény pedig egy adott eredménygyűjtemény. Az eseményeket általában az eredmények közös jellemzőjével írják le.
alkalmazzuk ezt a nyelvet, hogy lássuk, hogyan működnek a kifejezések a gyakorlatban. Egyes játékok igényelnek gördülő die hat oldalán, számozott 1 hogy 6. (A kocka a die többes száma.,) Az alábbi ábra szemlélteti a próbaverzió, az eredmény és az esemény használatát egy ilyen játékhoz:
vegye figyelembe, hogy az eredmények gyűjteményét zárójelbe helyezik és vesszővel elválasztják.
egy egyszerű esemény olyan esemény, amelynek csak egy eredménye van. Az 1 gördítése egyszerű esemény lenne, mert csak egy eredmény működik—1! Gördülő több mint 5 is lenne egy egyszerű esemény,mert az esemény csak 6 érvényes eredmény. Az összetett esemény egy olyan esemény, amelynek egynél több eredménye van. Például egy hatoldalas szerszám gördülése esetén a három eredmény egyikével páros szám is bekövetkezhet: 2, 4 és 6.,
Ha egy hatoldalas die-t sokszor gördít, akkor nem számíthat arra, hogy bármilyen eredmény gyakrabban fordul elő, mint a másik (feltételezve, hogy ez tisztességes halál). Az eredmények egy ilyen helyzetben azt mondják, hogy egyformán valószínű. Nagyon fontos felismerni, ha az eredmények ugyanolyan valószínűek a valószínűség kiszámításakor. Mivel a gördülő próbaverzió minden eredménye ugyanolyan valószínű, akkor számíthat arra, hogy minden eredményt ![]() a tekercsek., Ez azt jelenti, hogy a tekercsek
a tekercsek., Ez azt jelenti, hogy a tekercsek ![]() a tekercsek közül 1,
a tekercsek közül 1, ![]() a tekercsek közül 2,
a tekercsek közül 2, ![]() a tekercsek közül 3, stb.
a tekercsek közül 3, stb.
a fonó négy egyenlő részre oszlik,mindegyik más színű, az alábbiak szerint. Amikor ezt a fonót fonják, a nyíl az egyik színre mutat. Az eredmények egyformán valószínűek?
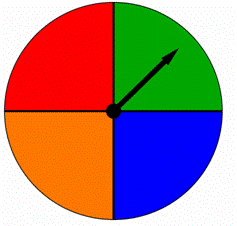
A) igen, ugyanolyan valószínűek.
B) nem, nem egyformán valószínűek.,
események valószínűsége
egy esemény valószínűsége az, hogy milyen gyakran várható. Ez az eseménytér méretének aránya a mintaterület méretéhez.
először meg kell határoznia a mintaterület méretét. A mintaterület mérete a lehetséges eredmények teljes száma. Például, ha tekercs 1 meghal, a minta tér 1, 2, 3, 4, 5, vagy 6. Tehát a mintaterület mérete 6.
ezután meg kell határoznia az eseménytér méretét., Az eseménytér az eredmények száma abban az esetben, ha érdekli. Az esemény helyet gördülő száma kevesebb, mint három 1 vagy 2. Tehát az eseménytér mérete 2.
hasonlóan valószínű eredmények esetén az e esemény valószínűsége P(E) lehet.
![]()
|
példa |
||
|
probléma |
a játék megköveteli gördülő egy hatoldalas szerszám számozott 1-6., Mi a valószínűsége annak, hogy páros számot gördít? |
|
|
Minta tér = {1, 2, 3, 4, 5, 6}
Esemény tér = {2, 4, 6} |
Először is, meg a minta tér, valamint a rendezvény tér. A mintaterület az összes lehetséges eredmény, az eseménytér pedig az esemény kimenetele. Ebben az esetben az esemény “páros számot gördít.,” |
|
|
|
Mivel az eredmények egyaránt valószínű, hogy a valószínűsége annak, hogy az esemény az arány esemény tér minta tér., |
|
|
Válasz |
P(páros szám) = |
|
Ez egy bevett gyakorlat a valószínűsége, mint a frakciók általános, hogy egyszerűsítse a valószínűsége a legalacsonyabb szempontjából, mivel így könnyebb a legtöbb ember, hogy érezd, hogy milyen jó. Hacsak nincs ok arra, hogy ezt ne tegye meg, fejezze ki az összes végső valószínűséget a legalacsonyabb értelemben.,
a fonó egyenlő részekre oszlik, mindegyik más színű, az alábbiak szerint., Megtalálni a valószínűsége annak, hogy a spinning kék vagy zöld ezen a spinner:
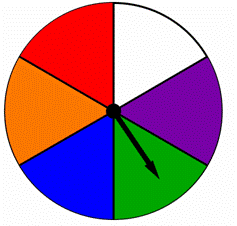
A) ![]()
B) ![]()
C) 2
D) 6
Számlálási Módszer, hogy megtalálja a Minta Terek
A legnehezebb kiszámításához valószínűséggel lehet találni a mintát hely, különösen akkor, ha két vagy több vizsgálatok. Számos számlálási módszer segíthet.,
az első, aki megnézi, diagramot készít. Az alábbi példában, Tori essek két érmét. Tehát gondosan meg kell határoznia a minta helyét. Egy olyan diagram, mint például a következő példában látható, jó megközelítés.
|
Példa |
||||
|
Probléma |
Tori essek egy pár érmét, majd megjegyezni, hogy sok fejtetőre a “fej” kap. Mi a valószínűsége annak, hogy 2 fejet ugrik?, Mi a valószínűsége annak, hogy csak 1 fejet hajt végre?,15ecf6″>T |
T |
TT |
|
sample space: {HH, HT, TH, TT}
event space for 2 heads: {HH}
event space for 1 head: {HT, TH}
Create a chart to record the results of flipping the first coin, followed by the result of flipping the second coin.,
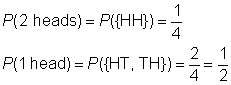
Mivel az eredmények egyaránt valószínű, hogy a valószínűsége annak, hogy az esemény az arány esemény tér minta tér.,
Válasz
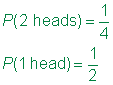
a példában a minta hely Tori egyszerű, mint egyetlen meghalni, hogy hengerelt. Mivel azonban James két halot gördít, egy diagram segít megszervezni az információkat.,
|
Példa |
||||||||
|
Probléma |
Tori hengerelt egy hat oldalas meghalni akartam, hogy egy eredmény, vagy 1, vagy 4. James két hatoldalas kockát forgatott, egy kéket és egy pirosat, és egyszerre egy 1-es és egy 3-as eredményt akart elérni. Melyik eseménynek nagyobb a valószínűsége?, |
|||||||
|
Tori’s sample space: {1, 2, 3, 4, 5, 6}
Tori’s event space: {1, 4}
Tori:
|
First, find the sample space and the event space for the two trials., Tori tárgyalására ez egyértelmű. mivel az eredmények egyformán valószínűek, az esemény valószínűsége az eseménytér aránya a mintaterülethez.,316594724″> 6 |
6,1 |
6,2 |
6,3 |
6,4 |
6,5 |
6,6 |
|
James’ sample space has 36 outcomes.,
James eseményterületének 2 kimenetele van.
Ez nem annyira nyilvánvaló James próba, mivel ő gördülő két kocka. Használja a diagramot a lehetőségek megtalálásához.
vannak 36 eredmények. Ezek közül 2 van, amelyek mind 1, mind 3.,
James: ![]()
Mivel az eredmények egyaránt valószínű, hogy a valószínűsége annak, hogy az esemény az arány esemény tér minta tér.
válasz
Tori eseményének nagyobb a valószínűsége.,
a minta helyének meghatározásához fa diagramot is használhat. A fa diagram egy ág minden lehetséges kimenetelét minden esemény.
tegyük fel, hogy a szekrényben három pár nadrág (fekete, fehér, zöld), négy ing (zöld, fehér, lila, sárga), és két pár cipő (fekete-fehér). Hány különböző ruhát lehet készíteni? 3 választás van a nadrághoz, 4 választás az inghez, 2 választás a cipőhöz., A fa diagramunkhoz használjuk a B-t fekete, w-t fehér, G-t Zöld, p-t lila, Y-t sárga esetén.
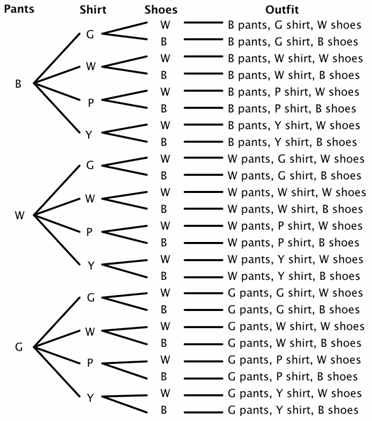
láthatjuk a fa diagram, hogy vannak 24 lehetséges ruhák (néhány talán nem nagy választás) a minta térben.
most már meglehetősen könnyen megoldhat néhány valószínűségi problémát. Például, mi a valószínűsége annak, hogy ha becsukja a szemét, és válasszon véletlenszerűen választaná nadrág, cipő, az azonos színű? Láthatjuk, hogy van 8 ruhák, ahol a nadrág és a cipő egyezik.,
![]()
mint láttuk, amikor egy próba több véletlenszerű elemet foglal magában, például egynél több érme elforgatásával vagy egynél több kocka gördítésével, nem mindig kell azonosítania a mintaterület minden eredményét a valószínűség kiszámításához. Csak az eredmények számára van szüksége.
Az alapvető számlálási elv egy módja annak, hogy megtaláljuk az eredmények számát anélkül, hogy felsorolnánk és megszámolnánk mindegyiket.,
Az alapvető számlálási elv
Ha egy eseménynek p lehetséges kimenetele van, egy másik eseménynek pedig m lehetséges kimenetele van, akkor a két esemény esetében összesen p • m lehetséges kimenetel van.
példák
* két hatoldalas kocka gördítése· minden egyes szerszámnak 6 ugyanolyan valószínű kimenetele van, tehát a mintaterület 6 • 6 vagy 36 ugyanolyan valószínű eredmény.
· essek három érmét: minden érme 2 egyformán valószínű eredmények, így a minta tér 2 • 2 • 2 vagy 8 egyformán valószínű eredmények.,
így használhatja az alapvető számlálási elvet, hogy megtudja, hány ruha van az előző példában. 3 választás van a nadrághoz, 4 választás az inghez, 2 választás a cipőhöz. Az alapvető számlálási elv használatával van 4 • 3 • 2 = 24 különböző ruhák.,
|
példa |
||
|
probléma |
Barry önkéntesek egy jótékonysági séta, hogy ebédet az összes többi önkéntes. Minden táskát tesz: · két szendvicset (mogyoróvajas, vagy pulyka, sajt), · egy három chips (rendszeres chips, sült krumpli, chips, vagy a chips kukorica), · egy darab gyümölcsöt (alma vagy narancs)., elfelejtette megjelölni, mi volt a zsákokban. Feltételezve, hogy minden választás egyformán valószínű, mi a valószínűsége annak, hogy a táska Therese kap tart egy mogyoróvaj, zselés szendvics és egy alma?, |
|
|
Size of sample space:
(number of sandwich choices) • (number of chip choices) • (number of fruit choices) = 2 • 3 • 2 = 12
|
First, use the Fundamental Counting Principle to find the size of the sample space., |
|
|
Méret esemény space:
(száma szendvics választási esemény) • (száma chip választási esemény) • (száma gyümölcs választási esemény) = |
az esemény tér, kövesse az elv ugyanaz. Ebben az esetben csak egy szendvics és egy darab érdekes gyümölcs van, de a háromféle Chip közül bármelyik elfogadható., |
|
|
válasz |
|
használja az arányt a valószínűség megtalálásához. |
Négy módja van, hogy pontosan egy farok: HHT, HHTH, HTHH, THHH, THHH. Mi a valószínűsége annak, hogy Carrie pontosan egy farkát kap?,
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Summary
Probability helps you understand random, unpredictable situations where multiple outcomes are possible., Ez az esemény valószínűségének mércéje, és az esemény és a lehetséges eredmények arányától függ, ha ezek az eredmények egyformán valószínűek.