a referenciaszög számológép használatához egyszerűen írjon be bármilyen szöget a szögdobozba, hogy megtalálja a referenciaszöget, amely az akut szög, amely megfelel a megadott szögnek. A számológép automatikusan alkalmazza az alábbiakban áttekintett szabályokat.
mi a referencia szög, egyébként?
Képzeljen el egy koordinátasíkot. Tegyük fel, hogy 144° – os szöget akarunk rajzolni a síkunkon., Az x tengely jobb oldalán kezdjük, ahol három óra van egy órán. Az óramutató járásával ellentétes irányba forgatunk,ami felfelé mozog. Tovább haladunk a 90°-os ponton (az y tengely felső részén), amíg 144° – ra nem jutunk. Rajzolunk egy sugarat az eredetből, amely a sík középpontja, addig a pontig. Most van egy sugár, amelyet a terminál oldalának hívunk. De még egy sugarat kell rajzolnunk, hogy szöget zárjunk. Most van választásunk. A második sugárnak a X-tengelyen kell lennie. Ha az eredetből a jobb oldalra húzzuk, akkor egy 144° – os szöget rajzolunk., Ha balra húzzuk, rajzolunk egy 36° – os szöget. Ez a második szög a referenciaszög. Ez mindig a kisebb a két szögből, mindig kisebb vagy egyenlő 90° – kal, és mindig pozitív lesz. Itt van egy animáció, amely megmutatja a referencia szög négy különböző szögek, amelyek mindegyike egy másik negyedben. Figyelje meg, hogy a második sugár mindig a x-tengelyen van.
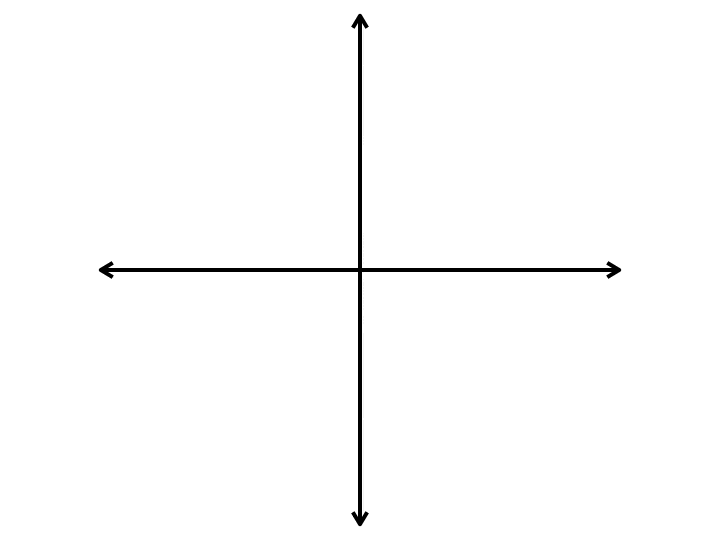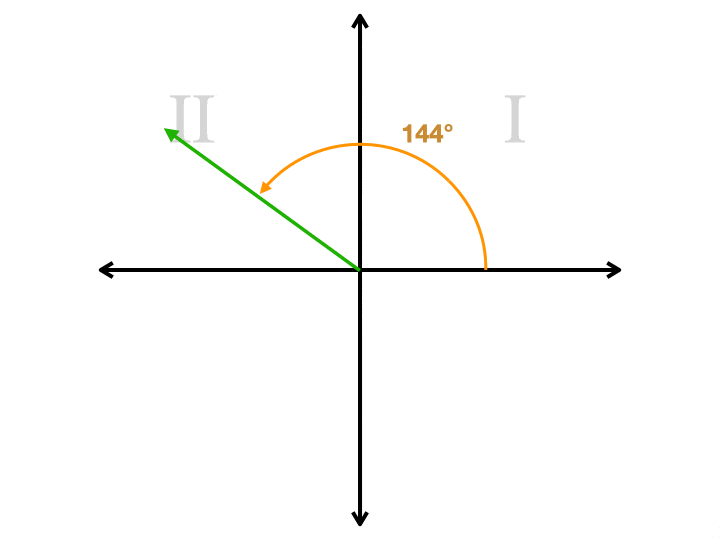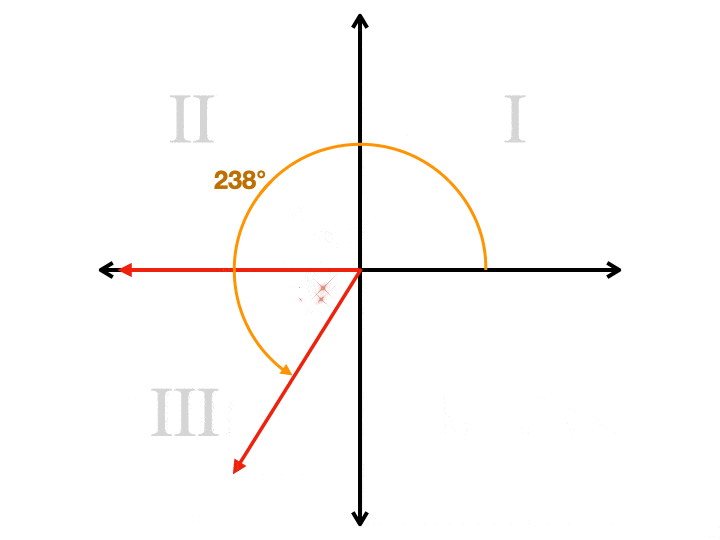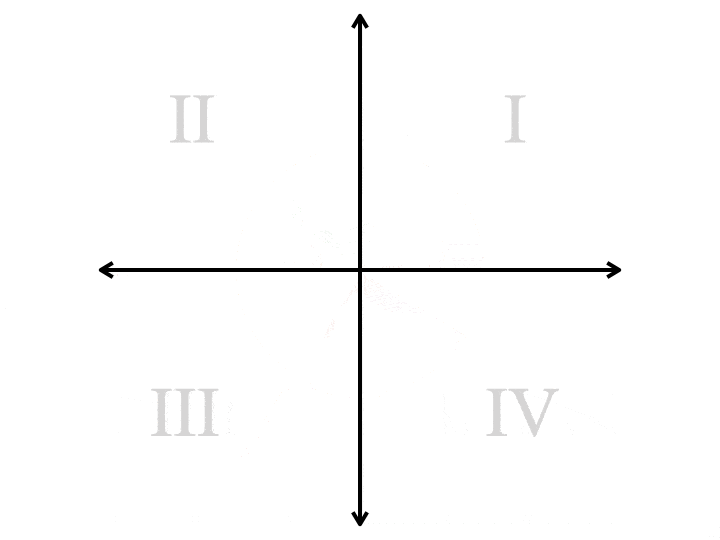
hogyan hasznos a Referenciaszög?
a referenciaszög mindig ugyanazokkal a trig függvényértékekkel rendelkezik, mint az eredeti szög. Figyeljük meg a szó értékeket ott., A jel nem lehet ugyanaz, de az érték mindig lesz. Ez hasznos a közös szögek, mint a 45° és 60°, hogy találkozunk újra és újra. Ha megismerjük szinusz, koszinusz és tangens értékeiket, akkor minden olyan szög értékeit is ismerjük, amelynek referenciaszöge szintén 45° vagy 60°. Ami a jelet illeti, ne feledje, hogy a szinusz pozitív az 1. és 2. kvadránsban, a koszinusz pedig pozitív az 1. és 4. kvadránsban.
Hogyan találjuk meg a referencia szöget számológép nélkül?
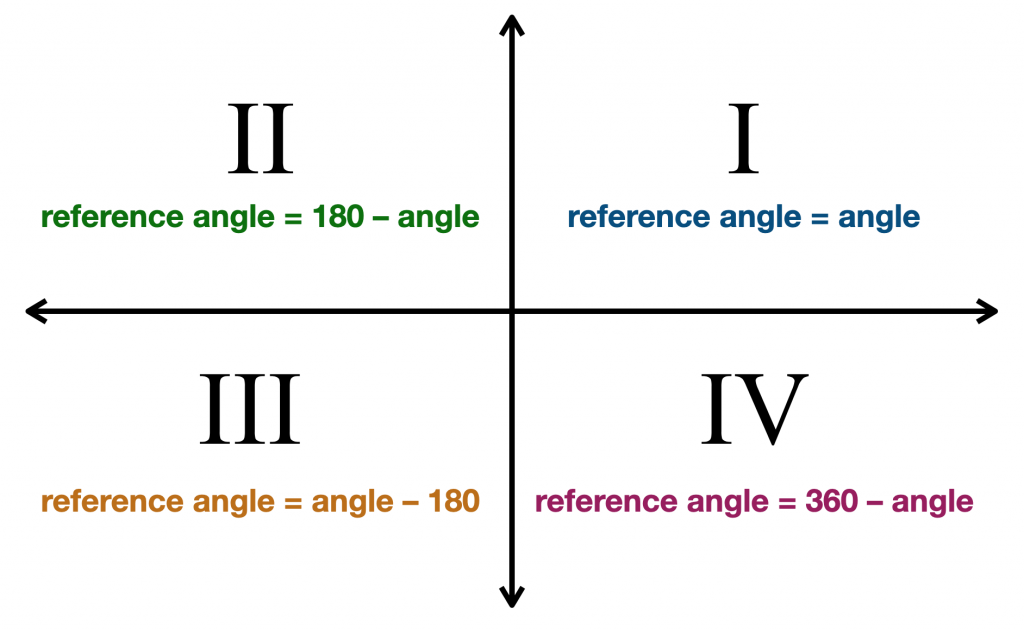
a referenciaszög megtalálása a terminál oldalának kvadránsától függ.,
amikor a terminál oldala az első kvadránsban van (szögek 0° – tól 90° – ig), referenciaszögünk megegyezik az adott szögünkkel. Ennek van értelme, mivel az első kvadráns összes szöge kevesebb, mint 90°. Tehát, ha az adott szögünk 33°, akkor referenciaszöge is 33°.
amikor a terminál oldala a második kvadránsban van (szögek 90° – tól 180° – ig), referenciaszögünk 180° mínusz az adott szög. Tehát, ha az adott szög 110°, akkor referenciaszöge 180° – 110° = 70°.,
amikor a terminál oldala a harmadik negyedben van (szögek 180° – tól 270° – ig), referenciaszögünk az adott szög mínusz 180°. Tehát, ha az adott szög 214°, akkor referenciaszöge 214° – 180° = 34°.
amikor a terminál oldala a negyedik kvadránsban van (szögek 270° – tól 360° – ig), referenciaszögünk 360° mínusz az adott szög. Tehát, ha az adott szög 332°, akkor referenciaszöge 360° – 332° = 28°.
mi van, ha Szögünk nagyobb, mint 360°?,
ha egy szög nagyobb, mint 360°, ez azt jelenti, hogy a koordináta síkja körül teljesen elfordult, és tovább haladt. A referenciaszög megtalálásához először meg kell találnunk a megfelelő szöget 0° és 360°között. Ezt könnyű megtenni. Csak 360-at vonunk le belőle, amíg 360 alá nem kerül. Például, ha a szögünk 544°, akkor 360° – ot vonunk le belőle, hogy megkapjuk 184° (544° – 360° = 184°). Most észrevennénk, hogy a harmadik kvadránsban van, ezért kivonnánk belőle 180° – ot, hogy megállapítsuk, hogy a referenciaszögünk 4°.
mi van, ha a Szögünk negatív?,
Ha egy szög negatív, akkor a másik irányt mozgatjuk, hogy megtaláljuk a terminál oldalunkat. Ez azt jelenti, hogy az óramutató járásával megegyező irányba mozogunk, nem pedig az óramutató járásával ellentétes irányba, amikor rajzoljuk. Vagy kiszámolhatjuk, egyszerűen hozzáadva 360° – ra. Például, ha az adott szögünk -110°, akkor hozzáadnánk 360° – hoz, hogy megtaláljuk az 250° (-110° + 360° = 250°). Most látnunk kell, hogy a harmadik kvadránsban vagyunk, és alkalmaznunk kell ezt a szabályt, hogy megtaláljuk a referenciaszögünket.(250° – 180° = 70°).