Public Key Encryption (Magyar)

Public Key Cryptography

ellentétben szimmetrikus kulcs kriptográfia, nem találjuk a nyilvános kulcsú kriptográfia történelmi használatát. Ez egy viszonylag új koncepció.

a szimmetrikus kriptográfia jól alkalmazható volt olyan szervezetek számára, mint a kormányok, a katonaság és a nagy pénzügyi vállalatok részt vettek a minősített kommunikációban.,

az elmúlt évtizedekben a biztonságosabb számítógépes hálózatok elterjedésével valódi szükség volt a kriptográfia nagyobb mértékű használatára. A szimmetrikus kulcs nem volt praktikus a kulcskezelés előtt álló kihívások miatt. Ez vezetett a nyilvános kulcs kriptosystems.

a Titkosítás és a dekódolás folyamatát a következő ábra mutatja −

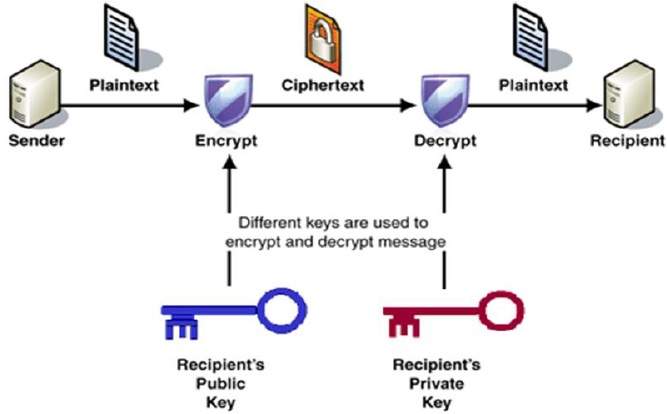
a nyilvános kulcs titkosítási rendszer legfontosabb tulajdonságai: −

• különböző kulcsokat használnak titkosításhoz és dekódoláshoz., Ez egy olyan tulajdonság, amely ezt a sémát különbözteti meg a szimmetrikus titkosítási sémától.

• minden vevő rendelkezik egy egyedi dekódolási kulccsal, amelyet általában privát kulcsának neveznek.

• a Vevőnek közzé kell tennie egy titkosítási kulcsot, amelyet nyilvános kulcsának neveznek.

• a nyilvános kulcs hitelességének bizonyos bizonyosságára van szükség ebben a rendszerben annak elkerülése érdekében, hogy az ellenfél mint vevő hamisítson. Általában az ilyen típusú kriptorendszer megbízható harmadik felet foglal magában, amely igazolja, hogy egy adott nyilvános kulcs csak egy adott személyhez vagy entitáshoz tartozik.,

• A titkosítási algoritmus elég összetett ahhoz, hogy a támadó ne vonja le a sima szöveget a titkosítási (nyilvános) kulcsból.

• bár a magán-és a nyilvános kulcsok matematikailag kapcsolódnak egymáshoz, a magánkulcsot nem lehet kiszámítani a nyilvános kulcsból. Valójában minden nyilvános kulcsú kriptorendszer intelligens része a két kulcs közötti kapcsolat megtervezése.

háromféle nyilvános kulcs titkosítási rendszer létezik., Megbeszéljük őket a következő szakaszokban –

RSA Cryptosystem

Ez a cryptosystem az egyik a kezdeti rendszer. Továbbra is a legtöbb alkalmazott kriptosystem még ma is. A rendszert három tudós, Ron Rivest, Adi Shamir és Len Adleman találta ki, ezért RSA kriptosystem-nek nevezik.

az RSA titkosítási rendszer két aspektusát fogjuk látni, először a kulcspár generálását, másodszor a titkosítási-dekódolási algoritmusokat.,

az RSA kulcspár generálása

minden olyan személynek vagy félnek, aki titkosítást használó kommunikációban kíván részt venni, egy pár kulcsot kell létrehoznia, nevezetesen a nyilvános kulcsot és a privát kulcsot. A folyamatot követte a generációs gombok az alábbiakban leírt −

• Generál az RSA modulus (n)

  • Válassza ki a két nagy prímszám, p, q.

  • számítsuk ki az n=p*q. Az erős feltörhetetlen titkosítás, legyen n egy nagy szám, általában minimum 512 bit.,

• derivált szám (e)

  • E számnak nagyobbnak kell lennie 1 − nél és kisebbnek, mint (P − 1)(q-1).

  • nem lehet közös tényező az e és (p − 1)(q − 1) esetében, kivéve az 1-et. Más szóval két szám e és (p-1) (q – 1) koprime.

• formálja a nyilvános kulcsot

  • A számpár (n, e) alkotja az RSA nyilvános kulcsot, és nyilvánosságra kerül.,

  • érdekes, hogy bár n része a nyilvános kulcsnak, a nagy prímszám faktorizálásának nehézsége biztosítja, hogy a támadó véges időben ne találja meg a két prímet (p & q), amelyet n. ez az RSA erőssége.

• Generál a privát kulcs

  • a Privát Kulcs d kiszámítása a p, q, valamint e. Adott n, e, egyedi szám d.

  • Szám d az inverz e modulo (p – 1)(q – 1)., Ez azt jelenti, hogy d a szám kisebb ,mint (p-1) (q – 1), hogy ha megszorozzuk e – vel, akkor egyenlő 1 modulo(P – 1) (q-1).

  • Ez a kapcsolat matematikailag a következőképpen íródott –

ed = 1 mod (p − 1)(q − 1)

a kiterjesztett euklideszi algoritmus P, q és e bemenetet ad, és D kimenetet ad.

példa

az alábbiakban egy példa az RSA kulcspár generálására. (A könnyebb megértés érdekében a p & q prímek kis értékek. Gyakorlatilag ezek az értékek nagyon magasak).,

• legyen két prím P = 7 és q = 13. Így modulus n = pq = 7 x 13 = 91.

• válassza ki az e = 5 értéket, amely érvényes választás, mivel nincs olyan szám, amely az 5 és (p − 1) közös tényezője(q− 1) = 6 × 12 = 72, kivéve az 1.

• a számpár (n, e) = (91, 5) képezi a nyilvános kulcsot, és bárki számára elérhetővé tehető, akinek titkosított üzeneteket szeretnénk küldeni nekünk.

• Input p = 7, q = 13 és e = 5 a kiterjesztett euklideszi algoritmushoz. A kimenet d = 29 lesz.,

• ellenőrizze, hogy a kiszámított d helyes −e számítástechnikával –

de = 29 × 5 = 145 = 1 mod 72

• ezért a nyilvános kulcs (91, 5) és a privát kulcsok (91, 29).

titkosítás és dekódolás

a kulcspár létrehozása után a Titkosítás és a dekódolás folyamata viszonylag egyszerű és számításigényes.

érdekes módon az RSA nem működik közvetlenül bit karakterláncokon, mint a szimmetrikus kulcs titkosítás esetén. Ez működik a számok modulo n. ezért szükséges, hogy képviselje a sima szöveg, mint egy sor szám kisebb, mint n.,

RSA titkosítás

• tegyük fel, hogy a feladó szöveges üzenetet szeretne küldeni valakinek, akinek nyilvános kulcsa (n, e).

• A feladónak akkor képviseli a plaintext, mint egy számsor kevesebb, mint n.

• titkosítja az első plaintext P, ami egy szám modulo n. A titkosítási folyamat egyszerű matematikai lépés, mint −

C = Pe mod n

• más szóval, a rejtjelezett C egyenlő a sima szövegként P szorozva magát, e-szor, majd csökkentett modulo n. Ez azt jelenti, hogy C is számos kisebb, mint n.,

• Vissza a Kulcs Generációs például a plaintext P = 10, kapunk rejtjelezett C −

C = 105 mod 91

RSA Dekódoló

• A dekódoló eljárás RSA is nagyon egyszerű. Tegyük fel, hogy a Vevő a nyilvános kulcs pár (n, e) kapott egy rejtjelezett C.

• Vevő emeli C a hatalom az ő privát kulcs d. az eredmény modulo n lesz a sima szövegű P.,

Plaintext = Cd mod n

• visszatérve a numerikus példánkhoz, a ciphertext C = 82 a 29 −

Plaintext = 8229 mod 91 = 10

RSA analízis

az RSA biztonsága két különálló funkció erősségeitől függ. Az RSA cryptosystem a legnépszerűbb nyilvános kulcsú kriptoszisztéma erőssége, amelynek alapja a nagyon nagy számok faktorálásának gyakorlati nehézsége.,

• Titkosítás Funkció − Úgy tekinthető, mint egy egyirányú függvény konvertálni a plaintext a rejtjelezett, illetve vissza lehet fordítani, csak a tudás, a privát kulcs d.

• Gombot Generáció − A nehéz meghatározása privát kulcs egy RSA nyilvános kulcs egyenértékű faktoring a modulus n. A támadó így nem használható tudás az RSA nyilvános kulcs meghatározásához RSA privát kulcsot, ha tud tényező n. Ez is egy módja a funkció, a p & q értékek modulus n könnyű, de visszafordítani nem lehet.,

Ha e két funkció közül bármelyik nem egyirányú, akkor az RSA megszakad. Valójában, ha hatékonyan fejlesztik a faktoring technikát, akkor az RSA már nem lesz biztonságos.

az RSA titkosítás erőssége drasztikusan csökken a támadások ellen, ha a P és q szám nem nagy prímek és / vagy az e nyilvános kulcs egy kis szám.

ElGamal Cryptosystem

az RSA mellett más nyilvános kulcsú kriptosystems is javasolt. Sokan közülük a diszkrét Logaritmusprobléma különböző verzióin alapulnak.,

az elliptikus görbe változatnak nevezett ElGamal kriptosystem a diszkrét Logaritmusproblémán alapul. Az erő abból a feltételezésből származik, hogy a diszkrét logaritmusok nem találhatók egy adott szám gyakorlati időkeretében, míg a teljesítmény inverz működése hatékonyan kiszámítható.

menjünk át egy egyszerű változata ElGamal, hogy működik a számok modulo p. abban az esetben, elliptikus görbe változatok, ez alapján egészen más számrendszerek.,

generációs ElGamal kulcspár

minden felhasználó ElGamal cryptosystem generálja a kulcspár az alábbiak szerint –

• kiválasztása nagy prime p. általában egy prímszám 1024-2048 bit hosszúságú van kiválasztva.

• generátor elem kiválasztása g.

  • ennek a számnak 1 és p − 1 között kell lennie, de nem lehet semmilyen szám.

  • Ez egy generátor a multiplikatív csoport egészek modulo p. Ez azt jelenti, minden egész M co-prime p, van egy egész k, hogy gk=a mod n.,

    például a 3 az 5. csoport generátora (Z5 = {1, 2, 3, 4}).

N	3n	3n mod 5
1	3	3
2	9	4
3	27	2
4	81	1

• Választott a privát kulcs. A privát kulcs x bármely szám nagyobb, mint 1 vagy kisebb, mint a p-1.

• a nyilvános kulcs számítási része., Az y értéket a P, g paraméterekből és az X privát kulcsból számítjuk ki az alábbiak szerint −

y = gx mod p

• nyilvános kulcs megszerzése. Az ElGamal nyilvános kulcs a három paraméterből áll (p, g, y).

  például tegyük fel, hogy p = 17 és G = 6 (megerősíthető, hogy a 6 a Z17 csoport generátora). A privát kulcs x lehet bármilyen szám nagyobb, mint 1, kisebb, mint 71, így választjuk x = 5. Az y értéket ezután a következőképpen számítjuk ki −

y = 65 mod 17 = 7

• így a privát kulcs 62, a nyilvános kulcs pedig (17, 6, 7).,

titkosítás és dekódolás

az ElGamal kulcspár generálása viszonylag egyszerűbb, mint az RSA egyenértékű folyamata. De a Titkosítás és a dekódolás valamivel összetettebb, mint az RSA.

ElGamal Titkosítással

Gondolom feladó kíván küldeni egy plaintext, hogy valaki, akinek az ElGamal nyilvános kulcs (p, g, y), akkor −

• Feladó képviseli a plaintext, mint egy számsor modulo p.

• titkosítja az első plaintext P, amely képviselteti magát, mint egy szám modulo p., A titkosítási folyamat megszerezni a rejtjelezett C a következők:

  • Véletlenszerűen generál egy szám k;
  • két Számítási értékek C1, illetve C2, ahol −

C1 = gk mod pC2 = (P*yk) mod p

• Küldés a rejtjelezett C, amely a két különálló értékek (C1, C2), küldött együtt.,

• Utalva az ElGamal kulcs generációs példa a fenti, a plaintext P = 13 titkosított, a következők:

  • Véletlenszerűen generál egy számot, mondjuk, k = 10
  • Kiszámolja a két érték C1, illetve C2, hol −

C1 = 610 mod 17C2 = (13*710) mod 17 = 9

• Küldés a rejtjelezett C = (C1, C2) = (15, 9).,

ElGamal Dekódoló

• visszafejteni a rejtjelezett (C1, C2) a privát kulcs x a következő két lépéseket −

  • Kiszámolja a moduláris inverze (C1)x modulo p, amely (C1)-x , általában a továbbiakban dekódoló tényező.,

  • szerezze be a sima szöveget a következő képlet segítségével: −

C2 × (C1)-x mod p = Plaintext

• példánkban a titkosítási tényező

15-5 mod 17 = 9

• kivonat plaintext P = (9 × 9) mod 17 = 13.

ElGamal Analysis

az ElGamal rendszerben minden felhasználónak van egy privát kulcsa x. és három összetevője van a public key-prime modulusnak − a G generátornak és a public Y = gx mod p., Az ElGamal erőssége a diszkrét logaritmus problémájának nehézségén alapul.

a biztonságos kulcsméret általában > 1024 bit. Ma még 2048 bit hosszú kulcsot is használnak. A feldolgozási sebesség fronton az Elgamal meglehetősen lassú, elsősorban a kulcsfontosságú hitelesítési protokollokhoz használják. A nagyobb feldolgozási hatékonyság miatt az ElGamal elliptikus görbe változatai egyre népszerűbbek.,

Elliptic Curve Cryptography (ECC)

Elliptic Curve Cryptography (ECC) egy olyan kifejezés, amelyet kriptográfiai eszközök és protokollok csomagjának leírására használnak, amelyek biztonsága a diszkrét logaritmusprobléma speciális verzióin alapul. Nem használ számok modulo p.

ECC alapul halmazok számok, amelyek társított matematikai objektumok úgynevezett elliptikus görbék. A számok többszörösének hozzáadására és kiszámítására is vannak szabályok, csakúgy, mint a számok modulo p esetében.,

az ECC számos olyan kriptográfiai rendszer változatát tartalmazza, amelyeket eredetileg moduláris számokra terveztek, mint például az ElGamal titkosítás vagy a digitális aláírás algoritmusa.

úgy gondolják, hogy a diszkrét logaritmusprobléma sokkal nehezebb, ha elliptikus görbe pontjaira alkalmazzák. Ez kéri váltás számok modulo p pont egy elliptikus görbe. Szintén azonos biztonsági szint érhető el rövidebb gombokkal, ha elliptikus görbe alapú változatokat használunk.,

A rövidebb kulcsok eredményeképpen két előnyök −

• Könnyű kulcs menedzsment
• Hatékony számítás

Ezek az előnyök, hogy elliptikus-görbe-alapú változatai titkosító program igen vonzó alkalmazás, ahol a számítástechnikai erőforrások korlátozottak.

RSA és ElGamal sémák-összehasonlítás

röviden hasonlítsuk össze az RSA és az ElGamal sémákat a különböző szempontokból.

RSA	ElGamal
ez hatékonyabb titkosítás.	ez hatékonyabb dekódolás.,
kevésbé hatékony a dekódoláshoz.	ez hatékonyabb dekódolás.
egy adott biztonsági szinthez hosszadalmas kulcsokra van szükség az RSA-ban.	ugyanazon biztonsági szinthez nagyon rövid kulcsokra van szükség.
széles körben elfogadott és használt.	új és nem túl népszerű a piacon.