Correlational Kutatás: Kérő Kapcsolatok Változók Között
ezzel szemben A leíró kutatás, amelynek célja elsősorban biztosítani statikus kép, correlational kutatás magában foglalja a mérés két vagy több releváns változók értékelése közötti kapcsolat, vagy azok között, változók., Például a magasság és a súly változói szisztematikusan összefüggenek (korrelálnak), mivel a magasabb emberek általában nagyobb súlyúak, mint a rövidebb emberek. Ugyanígy a tanulmányi idő és a memóriahibák is összefüggnek, mivel minél több időt kapnak egy személy a szavak listájának tanulmányozására, annál kevesebb hibát fog tenni. Ha két változó van a kutatási tervben, az egyiket prediktor változónak, a másik pedig eredményváltozónak nevezik., A kutatási design is megjeleníthető, mint ez, ahol az íves nyíl jelöli a várt összefüggés a két változó:
Ábra 2.2.2

Így a szervező az adatokat egy correlational tanulmány két változók grafikon az értékek az egyes mért változók segítségével egy scatter plot. Amint az a 2.10. ábrán látható “példák a Scatter parcellákra”, a scatter telek a két változó közötti kapcsolat vizuális képe., Egy pont van ábrázolva minden egyes metszéspontjában ő pontszámok a két változó. Amikor a scatter-telken lévő változók közötti összefüggés könnyen közelíthető egyenes vonallal, mint a 2.10. ábra A) és b) részében “szórási parcellák példái”, a változók lineáris összefüggést mutatnak.
amikor az egyenes azt jelzi, hogy azok az egyének, akiknek egy változó átlag feletti értékei vannak, általában a másik változó átlag feletti értékei is vannak, mint az a) részben, a kapcsolat pozitív lineáris., A pozitív lineáris kapcsolatok közé tartoznak például a magasság és a súly, az oktatás és a jövedelem, valamint a gyermekek életkora és matematikai képességei. Minden esetben az emberek, akik pontszám magasabb az egyik változó is hajlamosak a pontszám magasabb a másik változó. Ezzel szemben a negatív lineáris kapcsolatok, amint azt a B) rész mutatja, akkor fordulnak elő, ha egy változó átlag feletti értékei általában a másik változó átlag alatti értékeihez kapcsolódnak., A negatív lineáris kapcsolatok közé tartoznak például a gyermek életkora és a gyermek által használt pelenkák száma, valamint a tanulási feladatokkal kapcsolatos gyakorlatok és hibák. Ezekben az esetekben az emberek, akik pontszám magasabb az egyik változó általában pontszám alacsonyabb a másik változó.
az egyenes vonallal nem leírható változók közötti kapcsolatokat nemlineáris kapcsolatoknak nevezzük. Rész (c) ábra 2.10 “példák Scatter parcellák” azt mutatja, egy közös minta, amelyben az eloszlása a pontok lényegében véletlenszerű., Ebben az esetben egyáltalán nincs kapcsolat a két változó között, és azt mondják, hogy függetlenek. A 2.10. ábra d) és e) pontjai “szórási parcellák példái” olyan asszociációs mintákat mutatnak, amelyekben bár van társulás, a pontokat egyetlen egyenes nem írja le jól. A D) rész például azt mutatja, hogy milyen típusú kapcsolat áll fenn a szorongás és a teljesítmény között., Az alacsony-közepes szintű szorongás növekedése a teljesítmény növekedésével jár, míg a közepes-magas szintű szorongás növekedése a teljesítmény csökkenésével jár. Azok a kapcsolatok, amelyek irányt változtatnak, így egyetlen egyenes vonal nem írja le, görbe vonalú kapcsolatoknak nevezzük.
2.10 Ábra Példák a Scatter Telkek
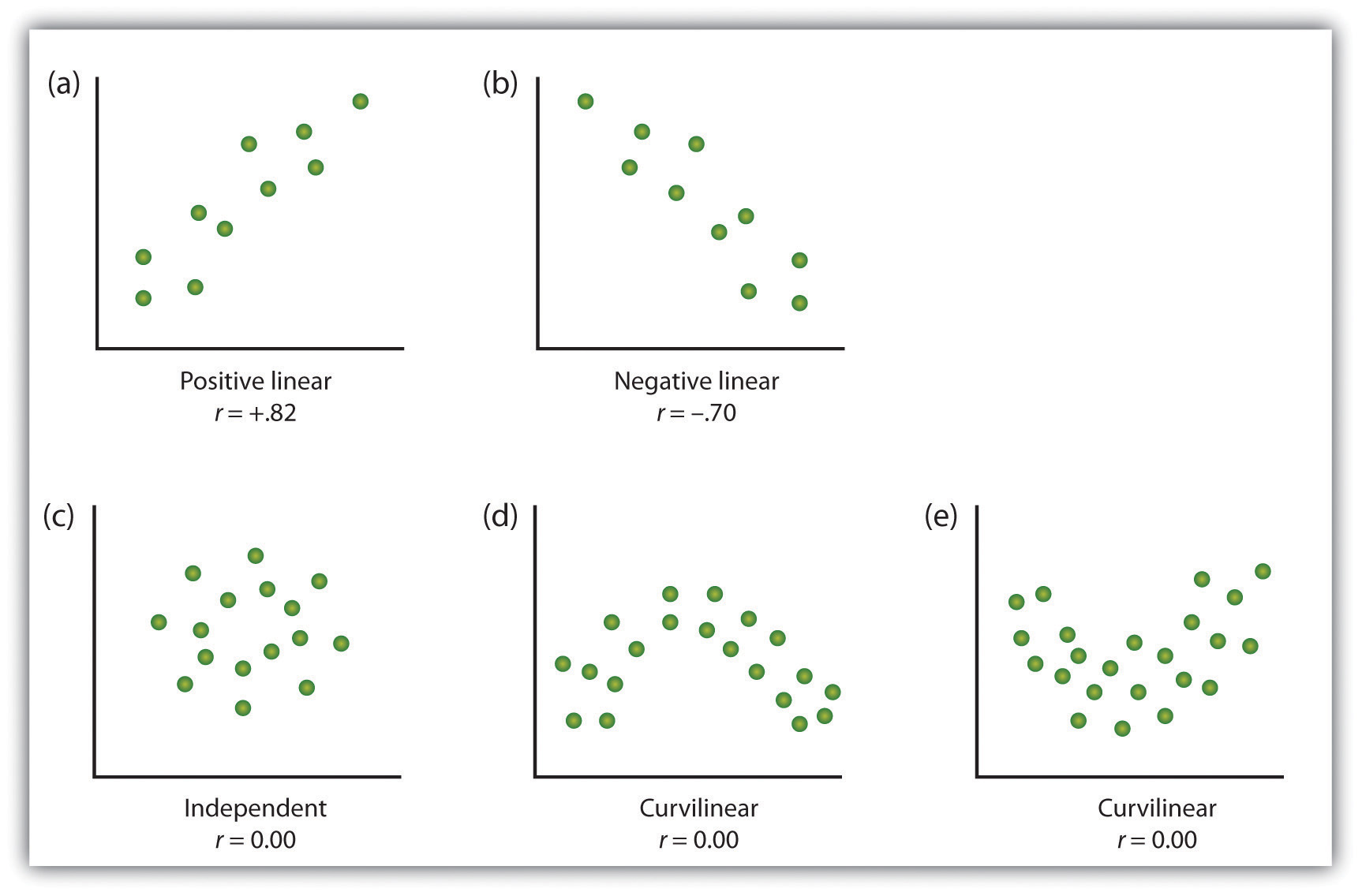
Néhány példa a kapcsolat a két változó amint azt a scatter telkek., Vegye figyelembe, hogy a Pearson korrelációs együttható (r) a görbületi kapcsolatokkal rendelkező változók között valószínűleg közel lesz a nullához.
adaptált Stangor, C. (2011). Kutatási módszerek a viselkedési tudományok (4. Szerk.). Mountain View, CA: Cengage.
a változók közötti lineáris kapcsolatok erősségének leggyakoribb statisztikai mércéje a Pearson korrelációs együttható,amelyet az r betű jelöl. a korrelációs együttható értéke r = -1,00-r = + 1,00., A lineáris kapcsolat irányát a korrelációs együttható jele jelzi. Az r pozitív értékei (például r = .54 vagy r = .67) jelezze, hogy a kapcsolat pozitív lineáris (azaz a scatter telken lévő pontok mintája a bal alsó és a jobb felső sarokban fut), míg az R negatív értékei (például r = -.30 vagy r = -.72) jelezze a negatív lineáris kapcsolatokat(azaz a pontok a bal felsőtől a jobb alsó részig futnak). A lineáris kapcsolat erősségét a korrelációs együttható nullától való távolsága (abszolút értéke) indexálja., Például r = -.54 erősebb kapcsolat, mint r = .30, és r = .72 erősebb kapcsolat, mint r = -.57. Mert a Pearson korrelációs együttható csak intézkedéseket lineáris kapcsolatok, változók, amelyek hengeres kapcsolatok nem jól leírható r, valamint a megfigyelt összefüggés közel lesz nulla.
egyidejűleg több mint két intézkedés közötti kapcsolatok tanulmányozása is lehetséges., Egy olyan kutatási terv, amelyben egynél több prediktorváltozót használnak egyetlen eredményváltozó előrejelzésére, többszörös regresszióval elemezzük (Aiken & West, 1991). A többszörös regresszió egy statisztikai technika, amely a változók közötti korrelációs együtthatókon alapul, amely lehetővé teszi egyetlen eredményváltozó előrejelzését egynél több prediktor változóból. Például a 2.11. ábra “a munka teljesítményének előrejelzése három Predictor változóból” egy többszörös regressziós elemzést mutat, amelyben három predictor változót használnak egyetlen eredmény előrejelzésére., A többszörös regressziós analízis használata a korrelációs kutatási tervek fontos előnyét mutatja—felhasználhatók arra, hogy előrejelzéseket készítsenek egy személy valószínű pontszámáról egy eredményváltozón (pl.
2.11.ábra a munka teljesítményének előrejelzése három Predictor változóból
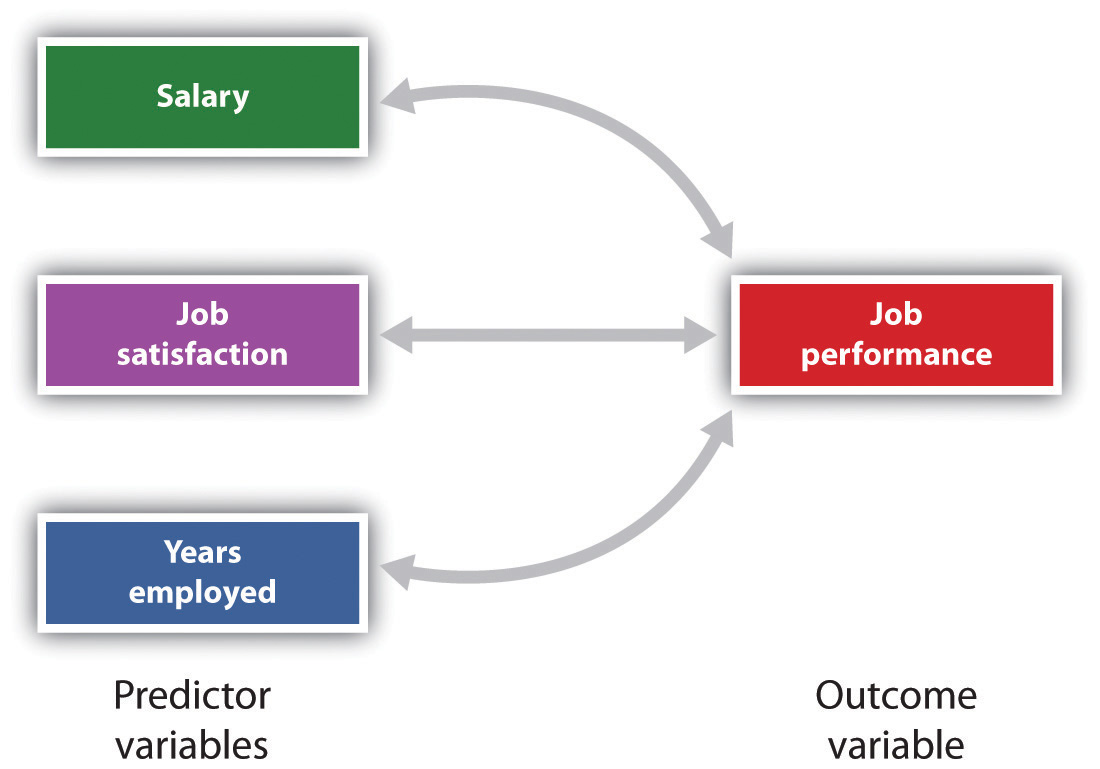
Több regresszió lehetővé teszi a tudósok számára, hogy egyetlen eredményváltozón a pontszámokat egynél több predictor változóval előre jelezzék.,
a korrelációs kutatási tervek fontos korlátozása az, hogy nem használhatók arra, hogy következtetéseket vonjanak le a mért változók közötti okozati összefüggésekről. Vegyünk például egy kutatót, aki feltételezte, hogy az erőszakos viselkedés megtekintése fokozott agresszív játékot okoz a gyermekeknél. A negyedikes gyerekek mintájából összegyűjtötte, hogy hány erőszakos televízió mutatja be az egyes gyermekek nézeteit a hét folyamán, valamint azt, hogy mennyire agresszíven játszik minden gyermek az iskolai játszótéren., Összegyűjtött adataiból a kutató pozitív korrelációt fedez fel a két mért változó között.
bár úgy tűnik, hogy ez a pozitív korreláció alátámasztja a kutató hipotézisét, nem lehet azt jelezni, hogy az erőszakos televíziózás agresszív viselkedést okoz. Bár a kutató hajlamos feltételezni, hogy az erőszakos televízió megtekintése agresszív játékot okoz,
2.2.2

> vannak más lehetőségek is., Az egyik alternatív lehetőség az, hogy az ok-okozati irány pontosan ellentétes a feltételezettekkel. Talán a gyerekek, akik agresszíven viselkedett az iskola fejleszteni maradék izgalom, ami a vezet őket akarom nézni erőszakos televízió-műsorok otthon:
Ábra 2.2.2

Bár ez a lehetőség, lehet, hogy úgy tűnik, kevésbé valószínű, ott nem lehet kizárni a lehetőségét, hogy az ilyen fordított ok-okozati összefüggés alapján a megfigyelt összefüggés., Az is lehetséges, hogy mindkét ok-okozati irányban működnek, valamint, hogy a két változó, mert egymást:
Ábra 2.2.2

Még egy másik lehetséges magyarázat, hogy a megfigyelt összefüggés, hogy készült a jelenléte egy közös-ok-okozati változó (úgy is ismert, mint egy harmadik változó)., A közös okozati változó olyan változó, amely nem része a kutatási hipotézisnek, hanem mind a prediktort, mind az eredményváltozót okozza, így a megfigyelt korrelációt hozza létre közöttük. Példánkban egy lehetséges közös okozati változó a gyermekek szüleinek fegyelemstílusa. A szülők, akik egy kemény, büntető fegyelem stílus okozhat a gyerekek, akik szeretik nézni, erőszakos televízió pedig, akik agresszíven viselkednek, összehasonlítva a gyerekek, akiknek a szülei használata kevésbé szigorú fegyelem:
Ábra 2.2.,2
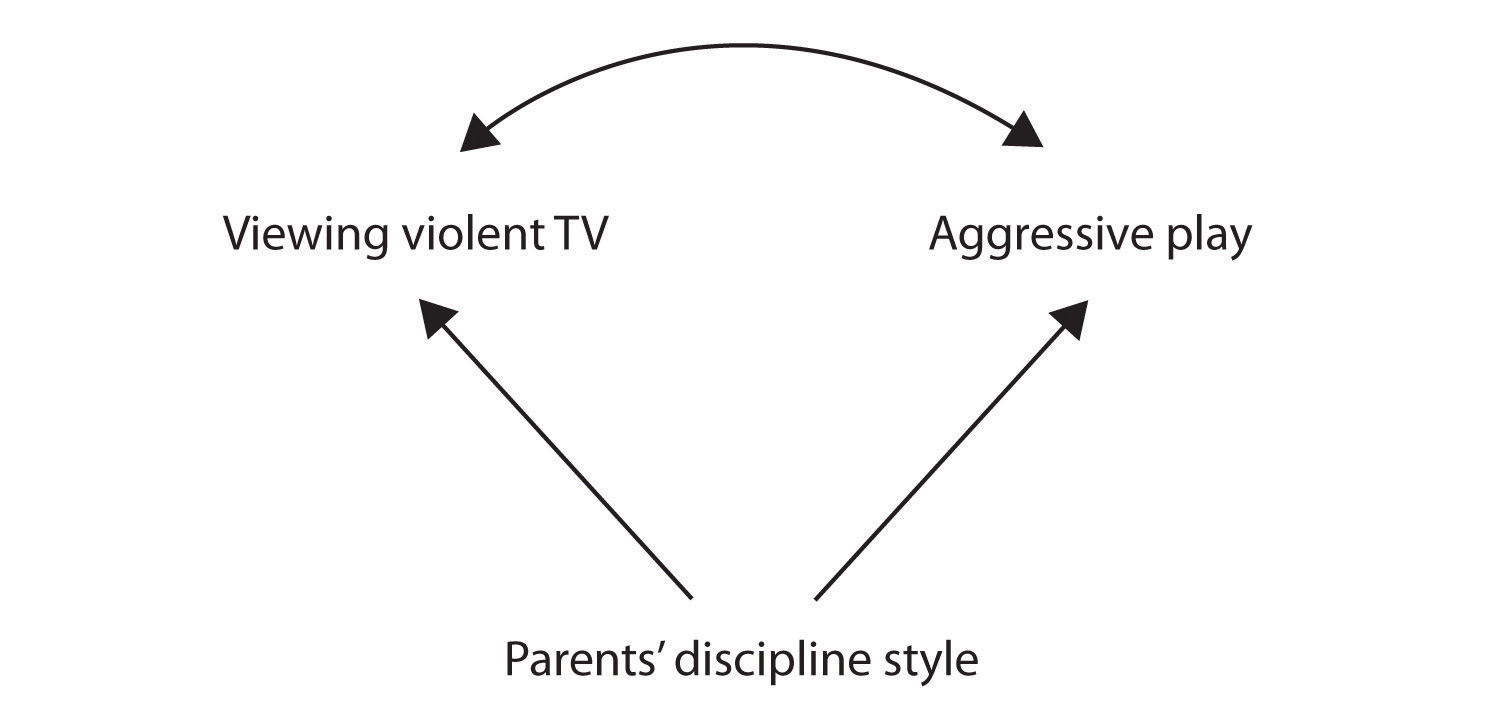
ebben Az esetben, televízió megtekintése, valamint agresszív játék pozitívan korrelált (ahogyan az íves nyíl között), bár egyik sem okozott, a másik, de mindketten okozta a fegyelem stílus, a szülők (az egyenes nyilak). Ha a prediktort és az eredményváltozókat egy közös okozati változó okozza, akkor a megfigyelt összefüggés hamisnak tekinthető., A hamis kapcsolat két változó közötti kapcsolat, amelyben egy közös okozati változó termel, és “magyarázza el” a kapcsolatot. Ha a közös ok-okozati változó hatásait elvennénk vagy ellenőriznénk, a prediktor és az eredményváltozók közötti kapcsolat eltűnne. A példában az agresszió és a tévénézés közötti kapcsolat azért lehet hamis, mert a szülők fegyelmezési stílusának hatására a tévénézés és az agresszív viselkedés közötti kapcsolat megszűnhet.,
a korrelációs kutatási tervekben a közös-okozati változókat “rejtély” változóknak lehet tekinteni, mivel nem mérték őket, jelenlétük és identitásuk általában ismeretlen a kutató számára. Mivel nem lehetséges minden olyan változó mérése, amely mind a prediktort, mind az eredményváltozókat okozhatja, egy ismeretlen közös-okozati változó létezése mindig lehetséges. Ezért a korrelációs kutatás alapvető korlátozásával maradunk: a korreláció nem bizonyítja az ok-okozati összefüggést., Fontos, hogy amikor a korrelációs kutatási projektekről olvas, ne feledje a hamis kapcsolatok lehetőségét, és ügyeljen arra, hogy a megállapításokat megfelelően értelmezze. Bár a korrelációs kutatásokat néha ok-okozati összefüggésnek bizonyítják anélkül, hogy megemlítenék a fordított ok-okozati vagy közös ok-okozati változók lehetőségét, tájékoztatták a fogyasztók a kutatásról, mint te, tisztában vannak ezekkel az értelmezési problémákkal.
összegezve, a korrelációs kutatási tervek mind erősségekkel, mind korlátozásokkal rendelkeznek., Az egyik erősség az, hogy akkor használhatók, ha a kísérleti kutatás nem lehetséges, mert a prediktor változókat nem lehet manipulálni. A korrelációs tervek előnye az is, hogy lehetővé teszik a kutató számára a viselkedés tanulmányozását a mindennapi életben. A korrelációs terveket arra is felhasználhatjuk, hogy előrejelzéseket készítsünk—például, hogy a tesztek akkumulátorának pontszámaiból megjósoljuk a gyakornokok sikerét egy edzés során. De nem használhatunk ilyen korrelációs információkat annak meghatározására, hogy a képzés jobb munkát eredményezett-e. Ehhez a kutatók kísérletekre támaszkodnak.,