Probabilité
l’Apprentissage Objectif(s)
· Définir les cas, l’issue du procès, simple événement, l’échantillon de l’espace et de calculer la probabilité qu’un événement se produise.
· Calculez la probabilité d’événements pour des résultats plus complexes.
· Résoudre des applications impliquant des probabilités.
Introduction
Probabilité fournit une mesure de la façon dont il est probable que quelque chose va se produire., C’est un nombre compris entre les nombres 0 et 1. Il peut être écrit comme une fraction, une décimale ou un pourcentage.

choisir des numéros au hasard signifie qu’il n’y a pas d’ordre précis dans lequel ils sont choisis. De nombreux jeux utilisent des dés ou des filateurs pour générer des nombres au hasard. Si vous comprenez comment calculer les probabilités, vous pouvez prendre des décisions réfléchies sur la façon de jouer à ces jeux en connaissant la probabilité de divers résultats.,
Définitions
d’Abord, vous devez connaître certains termes liés à la probabilité. Lorsque vous travaillez avec la probabilité, une action aléatoire ou une série d’actions est appelée un essai. Un résultat est le résultat d’un essai, et un événement est un ensemble particulier de résultats. Les événements sont généralement décrits en utilisant une caractéristique commune des résultats.
appliquons ce langage pour voir comment les Termes fonctionnent dans la pratique. Certains jeux nécessitent de lancer un dé avec six côtés, numérotés de 1 à 6. (Dés est le pluriel de mourir.,) Le tableau ci-dessous illustre l’utilisation de l’essai, du résultat et de l’événement pour un tel jeu:
notez qu’une collection de résultats est placée entre accolades et séparée par des virgules.
Un simple événement est un événement avec un seul résultat. Rouler un 1 serait un événement simple, car il n’y a qu’un seul résultat qui fonctionne—1! Rouler plus d’un 5 serait également un événement simple, car l’événement ne comprend que 6 comme résultat valide. Un composé est un événement à plus d’un résultat. Par exemple, en roulant un dé à six côtés, rouler un nombre pair pourrait se produire avec l’un des trois résultats: 2, 4 et 6.,
lorsque vous lancez un dé à six faces plusieurs fois, vous ne devez pas vous attendre à ce qu’un résultat se produise plus souvent qu’un autre (en supposant que c’est un dé équitable). On dit que les résultats dans une situation comme celle-ci sont tout aussi probables. Il est très important de reconnaître quand les résultats sont également probables lors du calcul de la probabilité. Étant donné que chaque résultat de l’essai die-rolling est également probable, vous vous attendez à obtenir chaque résultat ![]() des rouleaux., Qu’est que vous attendez
des rouleaux., Qu’est que vous attendez ![]() des rouleaux à 1,
des rouleaux à 1, ![]() des rouleaux à 2,
des rouleaux à 2, ![]() des rouleaux de 3, et ainsi de suite.
des rouleaux de 3, et ainsi de suite.
un spinner est divisé en quatre parties égales, chacune colorée avec une couleur différente comme indiqué ci-dessous. Lorsque ce spinner est tourné, la flèche pointe vers l’une des couleurs. Les résultats équiprobables?
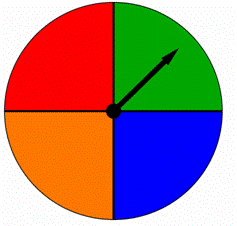
A) Oui, ils sont également probables.
B) non, ils ne sont pas aussi probables.,
la Probabilité d’Événements
La probabilité d’un événement est la façon dont souvent il est prévu de se produire. C’est le ratio de la taille de l’espace à la taille de l’échantillon de l’espace.
tout d’Abord, vous devez déterminer la taille de l’échantillon de l’espace. La taille de l’échantillon de l’espace est le nombre total de résultats possibles. Par exemple, lorsque vous lancez 1 dé, l’espace d’échantillon est 1, 2, 3, 4, 5, ou 6. La taille de l’espace d’échantillon est donc de 6.
Ensuite, vous devez déterminer la taille de l’espace événement., L’espace de l’événement est le nombre de résultats dans l’événement qui vous intéresse. L’espace d’événement pour rouler un nombre inférieur à trois est 1 ou 2. La taille de l’espace d’événement est donc de 2.
pour des résultats tout aussi probables, la probabilité d’un événement E peut s’écrire P(E).
![]()
|
Exemple |
||
|
Problème |
Un jeu nécessite de rouler à six faces mourir numérotées de 1 à 6., Quelle est la probabilité de rouler un nombre pair? |
|
|
Exemple de l’espace = {1, 2, 3, 4, 5, 6}
Événement d’espace = {2, 4, 6} |
tout d’Abord, trouver l’exemple de l’espace et de l’espace. L’exemple de l’espace est tous les résultats possibles, et de l’espace événement est le résultats de l’événement. Dans ce cas, l’événement est « rouler un nombre pair.,” |
|
|
|
Depuis, les résultats sont équiprobables, la probabilité de l’événement est le rapport de l’événement de l’espace de l’échantillon de l’espace., |
|
|
Réponse |
P(même numéro) = |
|
C’est une pratique courante avec des probabilités, que les fractions en général, pour simplifier, la probabilité en termes plus bas depuis qui le rend plus facile pour la plupart des gens de se faire une idée de comment il est grand. À moins qu’il n’y ait de raison de ne pas le faire, exprimez toutes les probabilités finales en termes les plus bas.,
un spinner est divisé en parties égales, chacune colorée avec une couleur différente comme indiqué ci-dessous., Trouvez la probabilité de tourner en bleu ou en vert sur cette fileuse:
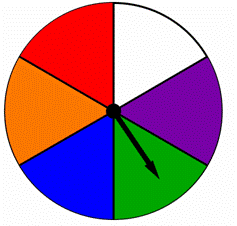
A) ![]()
B) ![]()
C) 2
D) 6
méthodes de comptage pour trouver des espaces d’échantillon
la chose la plus difficile pour calculer une probabilité peut être de trouver la taille de l’espace d’échantillon, Il existe plusieurs méthodes de comptage qui peuvent aider.,
le premier à regarder est de faire un graphique. Dans l’exemple ci-dessous, Tori retourne deux pièces. Vous devez donc déterminer l’espace d’échantillon avec soin. Un graphique tel que celui illustré dans l’exemple qui suit est une bonne approche.
|
Exemple |
||||
|
Problème |
Tori est en feuilletant une paire de pièces de monnaie et en notant la manière dont de nombreux retournements de « chefs” elle se. Quelle est la probabilité qu’elle retourne 2 têtes?, Quelle est la probabilité qu’elle retourne seulement 1 tête?,15ecf6 »>T |
T |
TT |
|
sample space: {HH, HT, TH, TT}
event space for 2 heads: {HH}
event space for 1 head: {HT, TH}
Create a chart to record the results of flipping the first coin, followed by the result of flipping the second coin.,
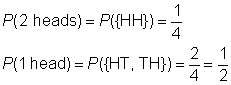
Depuis, les résultats sont équiprobables, la probabilité de l’événement est le rapport de l’événement de l’espace de l’échantillon de l’espace.,
Réponse
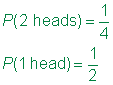
Dans l’exemple ci-dessous, l’exemple de l’espace pour Tori est simple comme un seul dé est lancé. Cependant, puisque James roule deux dé, un graphique aide à organiser l’information.,
|
Exemple |
||||||||
|
Problème |
Tori roulé un à six côtés de mourir et je voulais obtenir un résultat de 1 ou 4. James a lancé deux dés à six faces, un bleu et un rouge, et voulait obtenir un résultat à la fois 1 et 3, en même temps. Quel événement a une plus grande probabilité?, |
|||||||
|
Tori’s sample space: {1, 2, 3, 4, 5, 6}
Tori’s event space: {1, 4}
Tori:
|
First, find the sample space and the event space for the two trials., Pour le procès de Tori, c’est simple. Depuis, les résultats sont équiprobables, la probabilité de l’événement est le rapport de l’événement de l’espace de l’échantillon de l’espace.,316594724″> 6 |
6,1 |
6,2 |
6,3 |
6,4 |
6,5 |
6,6 |
|
James’ sample space has 36 outcomes.,
L’espace événementiel de James a 2 résultats.
Ce n’est pas si évident pour le procès de James, car il lance deux dés. Utilisez un graphique pour trouver les possibilités.
Il y a 36 résultats. Parmi ceux-ci, il y en a 2 qui ont à la fois 1 et 3.,
James: ![]()
Depuis, les résultats sont équiprobables, la probabilité de l’événement est le rapport de l’événement de l’espace de l’échantillon de l’espace.
Réponse
Tori, l’événement a une plus grande probabilité.,
Vous pouvez également utiliser une arborescence de déterminer l’échantillon de l’espace. Une arborescence est une branche pour chaque résultat possible pour chaque événement.
supposons qu’un placard comporte trois paires de pantalons (noir, blanc et vert), quatre chemises (vert, blanc, violet et jaune) et deux paires de chaussures (noir et blanc). Combien de tenues différentes peuvent être faites? Il y a 3 choix pour les pantalons, 4 choix pour les chemises et 2 choix pour les chaussures., Pour notre diagramme d’arbre, utilisons B pour le noir, W pour le blanc, G pour le vert, P pour le violet et Y pour le jaune.
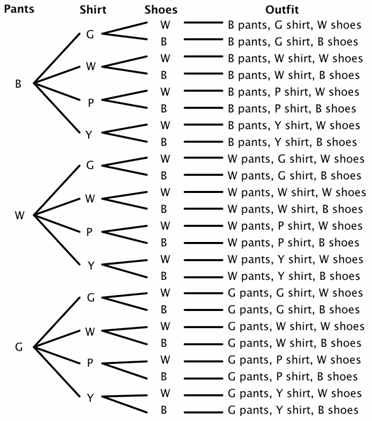
Vous pouvez voir dans l’arborescence qu’il y a 24 tenues possibles (certaines ne sont peut-être pas de grands choix) dans l’espace d’échantillon.
Maintenant, vous peut facilement résoudre certains problèmes probabilistes. Par exemple, Quelle est la probabilité que si vous fermez les yeux et choisissez au hasard, vous choisissiez des pantalons et des chaussures de la même couleur? Vous pouvez voir qu’il y a 8 tenues où le pantalon et les chaussures correspondent.,
![]()
Comme vous l’avez vu, lorsqu’un procès de plus d’un élément aléatoire, comme le retournement plus qu’une pièce ou rouler plus d’un dé, vous n’avez pas toujours besoin d’identifier tous les résultats de l’échantillon de l’espace pour calculer une probabilité. Vous avez seulement besoin du nombre de résultats.
Le principe fondamental de comptage est un moyen de trouver le nombre de résultats sans énumérer et Compter chacun d’eux.,
Les Fondamentaux de Comptage Principe
Si un événement a p résultats possibles, et un autre événement a m résultats possibles, alors il y a un total de p • m résultats possibles pour les deux événements.
exemples
· lancer deux dés à six faces: chaque dé a 6 Résultats également probables, donc l’espace d’échantillon est de 6 • 6 ou 36 résultats également probables.
· retournement de trois pièces: chaque pièce a 2 Résultats également probables, donc l’espace d’échantillon est 2 • 2 • 2 ou 8 résultats tout aussi probables.,
· lancer un dé à six faces et retourner une pièce de monnaie: l’espace de l’échantillon est de 6 • 2 ou 12 Résultats également probables.
Vous pouvez donc utiliser le principe de comptage fondamental pour savoir combien de tenues il y a dans l’exemple précédent. Il y a 3 choix pour les pantalons, 4 choix pour les chemises et 2 choix pour les chaussures. En utilisant le principe de comptage fondamental, vous avez 4 • 3 • 2 = 24 tenues différentes.,
|
Exemple |
||
|
Problème |
Barry volontaires à un organisme de bienfaisance à pied pour faire des repas pour tous les autres bénévoles. Dans chaque sac, il met: · l’un des deux sandwichs (beurre d’arachide et gelée, ou dinde et fromage), · l’un des trois chips (croustilles ordinaires, croustilles au four ou croustilles de maïs), · de fruits (une pomme ou une orange)., il a oublié de marquer ce qui était dans les sacs. En supposant que chaque choix est également probable, Quelle est la probabilité que le sac que Thérèse obtient contienne un sandwich au beurre de cacahuète et à la gelée et une pomme?, |
|
|
Size of sample space:
(number of sandwich choices) • (number of chip choices) • (number of fruit choices) = 2 • 3 • 2 = 12
|
First, use the Fundamental Counting Principle to find the size of the sample space., |
|
|
Taille de l’espace d’évènement:
(nombre de sandwich au choix de l’événement) • (numéro de puce de choix dans l’événement) • (nombre de fruits choix de l’événement) = |
Pour l’événement de l’espace, de suivre le même principe. Dans ce cas, il n’y a qu’un seul sandwich et un fruit d’intérêt, mais l’un des trois types de frites est acceptable., |
|
|
Réponse |
|
Utilisez un ratio de trouver la probabilité. |
Carrie flips de quatre pièces et compte le nombre de queues. Il y a quatre façons d’obtenir exactement une queue: HHHT, HHTH, HTHH et THHH. Quelle est la probabilité que Carrie obtienne exactement une queue?,
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Summary
Probability helps you understand random, unpredictable situations where multiple outcomes are possible., C’est une mesure de la probabilité d’un événement, et il dépend du rapport de l’événement et les résultats possibles, si tous ces résultats sont également probables.