recherche corrélationnelle: recherche de relations entre les Variables
contrairement à la recherche descriptive, qui est conçue principalement pour fournir des images statiques, la recherche corrélationnelle implique la mesure de deux variables pertinentes ou plus et une évaluation de la relation entre ces variables ou entre elles., Par exemple, les variables de taille et de poids sont systématiquement liées (corrélées) car les personnes plus grandes pèsent généralement plus que les personnes plus courtes. De la même manière, le temps d’étude et les erreurs de mémoire sont également liés, car plus une personne a le temps d’étudier une liste de mots, moins elle fera d’erreurs. Lorsqu’il y a deux variables dans le plan de recherche, l’une d’entre elles est appelée la variable prédictive et l’autre la variable de résultat., La conception de la recherche peuvent être visualisées comme cela, où la flèche courbe représente la corrélation entre les deux variables:
la Figure 2.2.2

Une façon d’organiser les données à partir d’une étude corrélationnelle avec deux variables est de graphe les valeurs de chacune des variables mesurées à l’aide d’un diagramme de dispersion. Comme vous pouvez le voir à la Figure 2.10 » exemples de diagrammes de dispersion”, un diagramme de dispersion est une image visuelle de la relation entre deux variables., Un point est tracé pour chaque individu à l’intersection de ses scores pour les deux variables. Lorsque l’association entre les variables sur le nuage de points peut être facilement approximée avec une ligne droite, comme dans les parties (a) et (b) de la Figure 2.10 « exemples de nuages de points”, les variables sont dites avoir une relation linéaire.
lorsque la ligne droite indique que les individus qui ont des valeurs supérieures à la moyenne pour une variable ont également tendance à avoir des valeurs supérieures à la moyenne pour l’autre variable, comme dans la partie (a), la relation est dite linéaire positive., Des exemples de relations linéaires positives incluent celles entre la taille et le poids, entre l’éducation et le revenu, et entre l’âge et les capacités mathématiques chez les enfants. Dans chaque cas, les personnes qui obtiennent un score plus élevé sur l’une des variables ont également tendance à obtenir un score plus élevé sur l’autre variable. Les relations linéaires négatives, en revanche, comme le montre la partie b), se produisent lorsque des valeurs supérieures à la moyenne pour une variable ont tendance à être associées à des valeurs inférieures à la moyenne pour l’autre variable., Des exemples de relations linéaires négatives incluent celles entre l’âge d’un enfant et le nombre de couches que l’enfant utilise, et entre la pratique et les erreurs commises sur une tâche d’apprentissage. Dans ces cas, les personnes qui obtiennent un score plus élevé sur l’une des variables ont tendance à obtenir un score plus bas sur l’autre variable.
Les relations entre les variables qui ne peuvent pas être décrites avec une ligne droite sont appelées relations non linéaires. La partie (c) de la Figure 2.10 « exemples de diagrammes de dispersion” montre un schéma commun dans lequel la distribution des points est essentiellement aléatoire., Dans ce cas, il n’y a aucune relation entre les deux variables, et elles sont dites indépendantes. Les Parties (d) et (e) de la Figure 2.10 « exemples de diagrammes de dispersion” montrent des schémas d’association dans lesquels, bien qu’il y ait une association, les points ne sont pas bien décrits par une seule ligne droite. Par exemple, la partie (d) montre le type de relation qui se produit fréquemment entre l’anxiété et la performance., L’augmentation de l’anxiété de niveaux faibles à modérés est associée à une augmentation des performances, tandis que l’augmentation de l’anxiété de niveaux modérés à élevés est associée à une diminution des performances. Les relations qui changent de direction et ne sont donc pas décrites par une seule ligne droite sont appelées relations curvilignes.
la Figure 2.10 Exemples de nuages de points
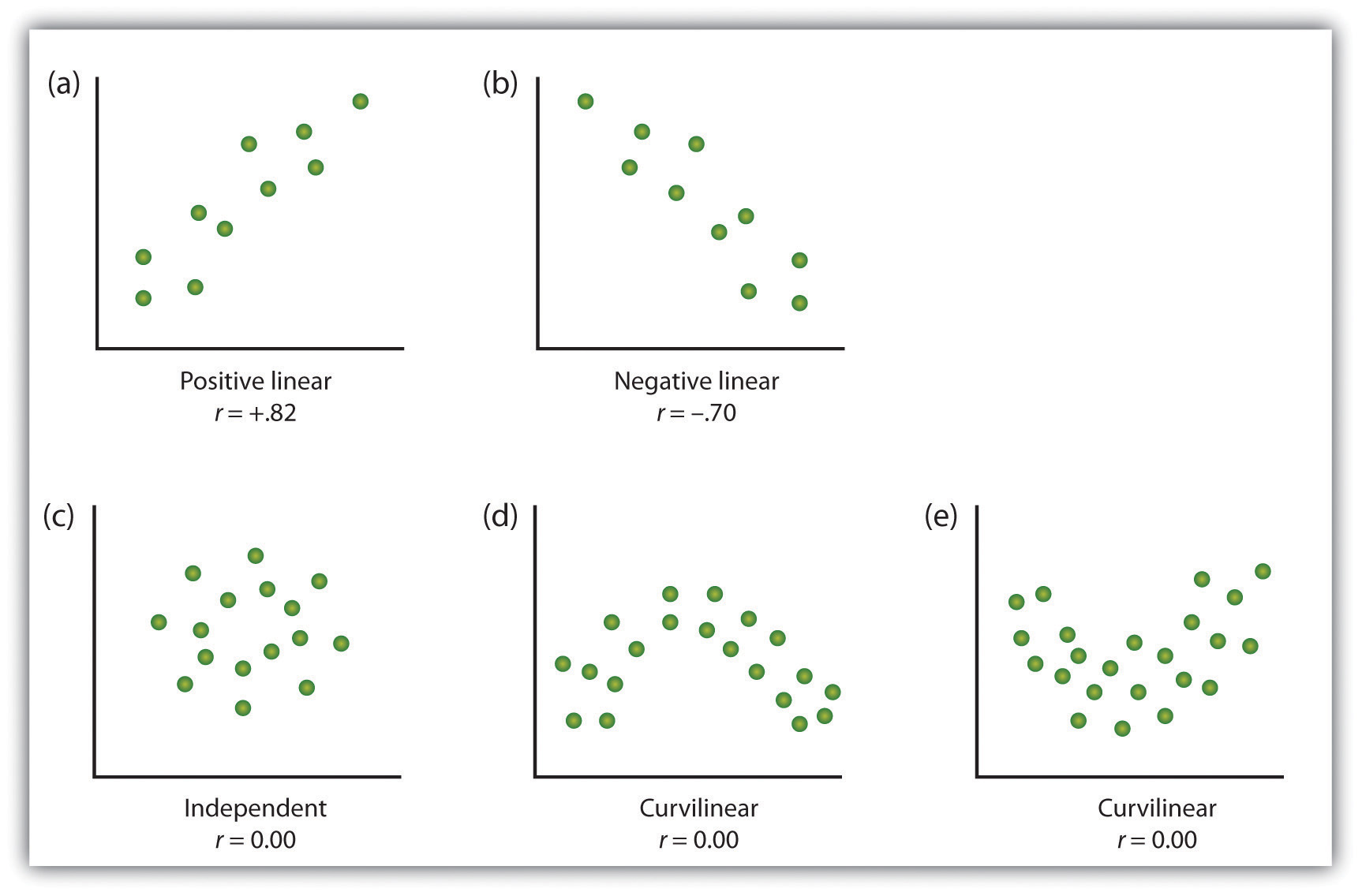
voici Quelques exemples de relations entre deux variables, comme indiqué dans les diagrammes de dispersion., Notez que le coefficient de corrélation de Pearson (r) entre les variables qui ont des relations curvilignes sera probablement proche de zéro.
Adapté de Stangor, C. (2011). Méthodes de recherche pour les sciences du comportement (4e éd.). Vue sur la montagne, Californie: Cengage.
la mesure statistique la plus courante de la force des relations linéaires entre variables est le coefficient de corrélation de Pearson, symbolisé par la lettre R. La valeur du coefficient de corrélation varie de r = -1,00 à r = +1,00. , La direction de la relation linéaire est indiquée par le signe du coefficient de corrélation. Valeurs positives de r (telles que r = .54 ou r = .67) indiquent que la relation est linéaire positive (c’est –à-dire que le motif des points sur le nuage de points va du bas à gauche au haut à droite), alors que les valeurs négatives de r (telles que r= -.30 ou r = –.72) indiquent les relations linéaires négatives (c’est-à-dire que les points vont du haut à gauche au bas à droite). La force de la relation linéaire est indexée par la distance du coefficient de corrélation de zéro (sa valeur absolue)., Par exemple, r = –.54 est une relation plus forte que r = .30, et r = .72 est une relation plus forte que r = –.57. Étant donné que le coefficient de corrélation de Pearson ne mesure que les relations linéaires, les variables qui ont des relations curvilignes ne sont pas bien décrites par r, et la corrélation observée sera proche de zéro.
Il est également possible d’étudier les relations entre plus de deux mesures en même temps., Un plan de recherche dans lequel plus d’une variable prédictive est utilisée pour prédire une seule variable de résultat est analysé par régression multiple (Aiken & West, 1991). La régression Multiple est une technique statistique, basée sur des coefficients de corrélation entre variables, qui permet de prédire une seule variable de résultat à partir de plus d’une variable prédictive. Par exemple, la Figure 2.11 « prédiction du rendement au travail à partir de trois Variables prédictives” montre une analyse de régression multiple dans laquelle trois variables prédictives sont utilisées pour prédire un seul résultat., L’utilisation de l’analyse de régression multiple montre un avantage important des conceptions de recherche corrélationnelles—elles peuvent être utilisées pour faire des prédictions sur le score probable d’une personne sur une variable de résultat (p. ex., le rendement au travail) en fonction de la connaissance d’autres variables.
Figure 2.11 prédiction de la Performance au travail à partir de trois Variables prédictives
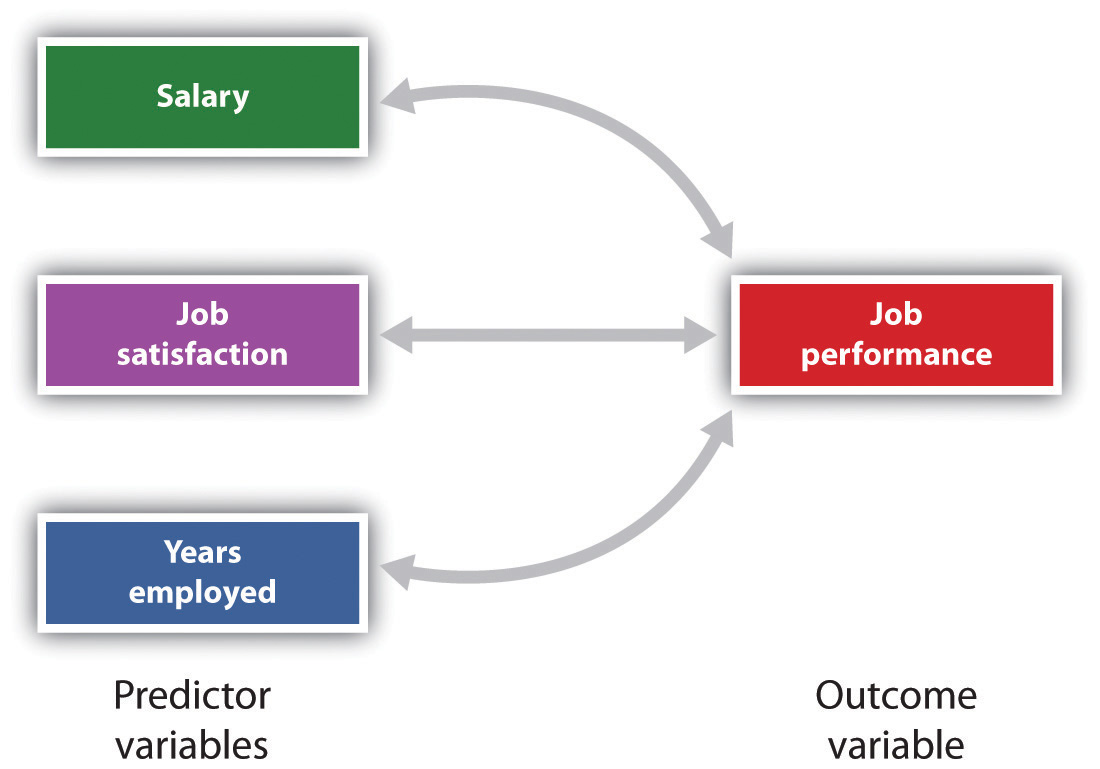
la régression Multiple permet aux scientifiques de prédire les scores sur une seule variable de résultat en utilisant plus d’un prédicteur variable.,
une limitation importante des plans de recherche corrélationnels est qu’ils ne peuvent pas être utilisés pour tirer des conclusions sur les relations causales entre les variables mesurées. Considérons, par exemple, un chercheur qui a émis l’hypothèse que la visualisation d’un comportement violent provoquerait une augmentation du jeu agressif chez les enfants. Il a recueilli, à partir d « un échantillon d » enfants de quatrième année, une mesure du nombre d « émissions de télévision violentes vues par chaque enfant au cours de la semaine, ainsi qu » une mesure de l « agressivité de chaque enfant joue sur le terrain de jeu de l » école., À partir de ses données collectées, le chercheur découvre une corrélation positive entre les deux variables mesurées.
bien que cette corrélation positive semble soutenir l’hypothèse du chercheur, elle ne peut pas être prise pour indiquer que regarder la télévision violente provoque un comportement agressif. Bien que le chercheur est tenté de penser que le visionnement de violentes à la télévision provoque de jeu agressif,
la Figure 2.2.2

il y a d’autres possibilités., Une autre possibilité est que la direction causale est exactement opposée à ce qui a été supposé. Peut-être que les enfants qui se sont comportés agressivement à l’école développent une excitation résiduelle qui les amène à vouloir regarder des émissions de télévision violentes à la maison:
Figure 2.2.2
 /div>
/div>
bien que cette possibilité puisse sembler moins probable, il n’y a aucun moyen d’exclure la possibilité d’une telle causalité inverse sur la base de cette corrélation observée., Il est également possible que les deux directions causales fonctionnent et que les deux variables se causent mutuellement:
Figure 2.2.2

Une autre explication possible de la corrélation observée est qu’elle a été produite par la présence d’une variable causale commune (également appelée troisième variable)., Une variable causale commune est une variable qui ne fait pas partie de l’hypothèse de recherche, mais qui provoque à la fois le prédicteur et la variable de résultat et produit ainsi la corrélation observée entre eux. Dans notre exemple, une variable causale commune potentielle est le style de discipline des parents des enfants. Les Parents qui utilisent un style de discipline sévère et punitive peuvent produire des enfants qui aiment regarder la télévision violente et qui se comportent de manière agressive par rapport aux enfants dont les parents utilisent une discipline moins dure:
Figure 2.2.,2
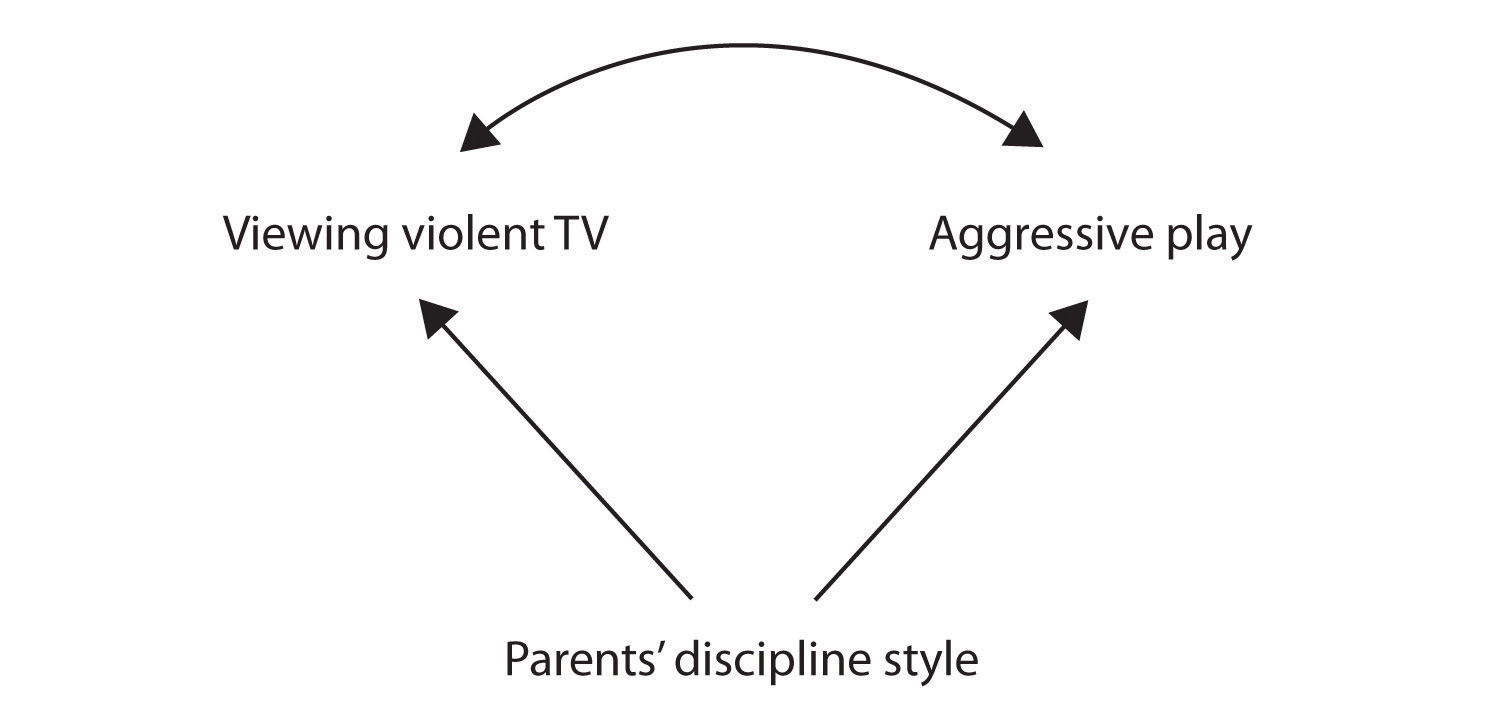
dans ce cas, l’écoute de la télévision et le jeu agressif seraient positivement corrélés (comme indiqué par la flèche incurvée entre eux), même si ni l’un ni l’autre ne causaient l’autre mais ils étaient tous deux causés par le style de discipline des parents (les flèches droites). Lorsque le prédicteur et les variables de résultat sont tous deux causés par une variable causale commune, la relation observée entre eux est dite fausse., Une relation fausse est une relation entre deux variables dans laquelle une variable causale commune produit et” explique » la relation. Si les effets de la variable causale commune étaient supprimés ou contrôlés, la relation entre le prédicteur et les variables de résultat disparaîtrait. Dans l’exemple, la relation entre l’agression et le visionnement de la télévision pourrait être fausse parce qu’en contrôlant l’effet du style de discipline des parents, la relation entre le visionnement de la télévision et le comportement agressif pourrait disparaître.,
Les variables causales communes dans les plans de recherche corrélationnels peuvent être considérées comme des variables « mystères” parce que, comme elles n’ont pas été mesurées, leur présence et leur identité sont généralement inconnues du chercheur. Comme il n’est pas possible de mesurer toutes les variables qui pourraient causer à la fois le prédicteur et les variables de résultat, l’existence d’une variable causale commune inconnue est toujours possible. Pour cette raison, nous nous retrouvons avec la limitation de base de la recherche corrélationnelle: la corrélation ne démontre pas la causalité., Il est important que lorsque vous lisez sur les projets de recherche corrélationnels, vous gardez à l’esprit la possibilité de relations fallacieuses, et assurez-vous d’interpréter les résultats de manière appropriée. Bien que la recherche corrélationnelle soit parfois rapportée comme démontrant la causalité sans qu’il soit fait mention de la possibilité d’une causalité inverse ou de variables causales communes, les consommateurs informés de la recherche, comme vous, sont conscients de ces problèmes d’interprétation.
en somme, les conceptions de recherche corrélationnelles ont à la fois des forces et des limites., Une force est qu’ils peuvent être utilisés lorsque la recherche expérimentale n’est pas possible parce que les variables prédictives ne peuvent pas être manipulées. Les conceptions corrélationnelles ont également l’avantage de permettre au chercheur d’étudier le comportement tel qu’il se produit dans la vie quotidienne. Et nous pouvons également utiliser des conceptions corrélationnelles pour faire des prédictions—par exemple, pour prédire à partir des scores de leur batterie de tests le succès des stagiaires au cours d’une session de formation. Mais nous ne pouvons pas utiliser de telles informations corrélationnelles pour déterminer si la formation a entraîné une meilleure performance au travail. Pour cela, les chercheurs s’appuient sur des expériences.,