de Cryptage de Clés Publiques

la Cryptographie à Clé Publique

Contrairement à la cryptographie à clé symétrique, nous ne trouvons pas l’utilisation historique de la cryptographie à clé publique. Il est un concept relativement nouveau.

la cryptographie symétrique était bien adaptée aux organisations telles que les gouvernements, les militaires et les grandes sociétés financières impliquées dans la communication classifiée.,

avec la propagation de plus en plus de réseaux informatiques non sécurisés au cours des dernières décennies, un véritable besoin s’est fait sentir d’utiliser la cryptographie à plus grande échelle. La clé symétrique a été jugée non pratique en raison des défis qu’elle rencontrait pour la gestion des clés. Cela a donné naissance aux cryptosystèmes à clé publique.

le processus de chiffrement et de déchiffrement est représenté dans l’illustration suivante −

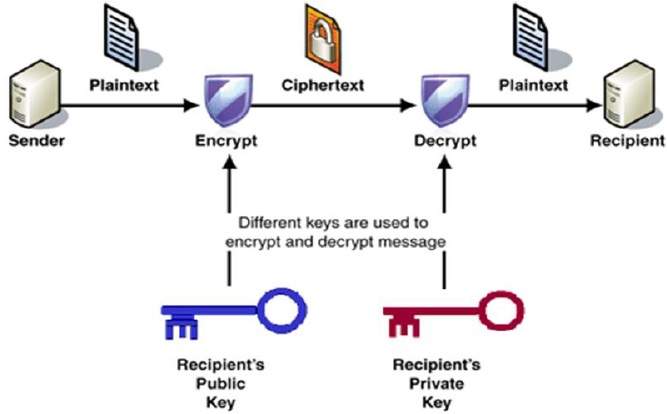
Les propriétés les plus importantes du schéma de chiffrement à clé publique sont −

• différentes clés sont utilisées pour le chiffrement et le déchiffrement., Il s’agit d’une propriété qui définit ce schéma différent du schéma de chiffrement symétrique.

• Chaque récepteur possède une unique clé de déchiffrement, généralement appelé sa clé privée.

• Récepteur doit publier une clé de chiffrement, appelé sa clé publique.

• l’assurance de l’authenticité de la clé publique est nécessaire dans ce schéma afin d’éviter l’usurpation par l’adversaire comme le récepteur. Généralement, ce type de cryptosystème implique un tiers de confiance qui certifie qu’une clé publique particulière appartient uniquement à une personne ou à une entité spécifique.,

• l’algorithme de chiffrement est suffisamment complexe pour empêcher l’attaquant de déduire le texte brut du texte chiffré et de la clé de chiffrement (publique).

• Bien que les clés privées et publiques sont liées mathématiquement, il n’est pas possible de calculer la clé privée de la clé publique. En fait, une partie intelligente de tout cryptosystème à clé publique consiste à concevoir une relation entre deux clés.

Il existe trois types de systèmes de Cryptage à Clé Publique., Nous en discutons dans les sections suivantes,

Cryptosystème RSA

Ce cryptosystème est l’un des système de départ. Il reste le cryptosystème le plus utilisé même aujourd’hui. Le système a été inventé par trois chercheurs Ron Rivest, Adi Shamir et Len Adleman et, par conséquent, il est appelé RSA cryptosystem.

nous verrons deux aspects du cryptosystème RSA, d’une part la génération de paires de clés et d’autre part les algorithmes de chiffrement-décryptage.,

génération D’une paire de clés RSA

chaque personne ou partie souhaitant participer à une communication utilisant le chiffrement doit générer une paire de clés, à savoir la clé publique et la clé privée. Le processus suivi dans la génération des clés est décrit ci −dessous –

• générer le module RSA (n)

  • sélectionner deux grands nombres premiers, p et Q.

  • calculer n=p*q. pour un chiffrement fort incassable, soit n Un grand nombre, typiquement un minimum de 512 bits.,

• Trouver Nombre Dérivé (e)

  • le Numéro de e doit être supérieur à 1 et inférieur à (p − 1)(q − 1).

  • il ne doit pas y avoir de facteur commun pour e et (p − 1)(q − 1) sauf pour 1. En d’autres termes deux nombres e et (p – 1)(q – 1) sont premiers entre eux.

• la Forme de la clé publique

  • La paire de nombres (n, e) de la forme de la clé publique RSA et est rendu public.,

  • fait intéressant, bien que n fasse partie de la clé publique, la difficulté à factoriser un grand nombre premier garantit que l’attaquant ne peut pas trouver en temps fini les deux nombres premiers (p & q) utilisés pour obtenir N. c’est la force de RSA.

• Générer la clé privée

  • la Clé Privée d est calculée à partir de p, q et e. Pour n et e, il est numéro unique d.

  • Nombre d est l’inverse de e modulo (p – 1)(q – 1)., Cela signifie que d est le nombre inférieur à (p – 1) (q – 1) tel que multiplié par e, il est égal à 1 modulo(p – 1) (q-1).

  • Cette relation s’écrit mathématiquement comme suit:

ed = 1 mod (p − 1)(q − 1)

L’Algorithme d’Euclide Étendu prend p, q et e comme entrée et donne d en sortie.

exemple

un exemple de génération D’une paire de clés RSA est donné ci-dessous. (Pour faciliter la compréhension, les nombres premiers p & q pris ici sont de petites valeurs. Pratiquement, ces valeurs sont très élevées).,

• supposons que deux nombres premiers p = 7 et q = 13. Ainsi, module n = pq = 7 x 13 = 91.

• sélectionnez e = 5, ce qui est un choix valide car il n’y a pas de nombre qui est un facteur commun de 5 et (p-1) (q− 1) = 6 × 12 = 72, sauf pour 1.

• la paire de nombres (n, e) = (91, 5) forme la clé publique et peut être mise à la disposition de toute personne à qui nous souhaitons pouvoir nous envoyer des messages chiffrés.

• entrez p = 7, q = 13 et e = 5 dans l’algorithme euclidien étendu. La sortie sera d = 29.,

• Vérifiez que le d calculé est correct en informatique

de = 29 × 5 = 145 = 1 mod 72

• par conséquent, la clé publique est (91, 5) et des clés privées est (91, 29).

chiffrement et déchiffrement

Une fois la paire de clés générée, le processus de chiffrement et de déchiffrement est relativement simple et facile à calculer.

fait intéressant, RSA n’opère pas directement sur des chaînes de bits comme dans le cas du chiffrement à clé symétrique. Il fonctionne sur des nombres modulo N. Par conséquent, il est nécessaire de représenter le texte en clair comme une série de nombres inférieurs à N.,

de Cryptage RSA

• Supposons que l’expéditeur souhaite envoyer un message texte à quelqu’un dont la clé publique (n, e).

• l’expéditeur représente alors le texte en clair comme une série de nombres inférieurs à N.

• pour chiffrer le premier texte en clair P, qui est un nombre modulo N. le processus de chiffrement est simple étape mathématique comme −

C = Pe mod n

e texte en clair P multiplié par lui-même e fois, puis réduit modulo N. cela signifie que c est également un nombre inférieur à N.,

• En revenant à notre exemple de génération de clé avec le texte en clair P = 10, nous obtenons le texte chiffré C −

C = 105 mod 91

RSA Decryption

• le processus de déchiffrement pour RSA est également très simple. Supposons que le récepteur de la paire de clés publiques (n, e) ait reçu un texte chiffré C.

• Le récepteur élève C à la puissance de sa clé privée d. le résultat modulo n sera le texte en clair P.,

Plaintext = Cd mod n

• revenant à notre exemple numérique, le texte chiffré C = 82 serait déchiffré au numéro 10 en utilisant la clé privée 29 −

Plaintext = 8229 mod 91 = 10

analyse RSA

la sécurité de RSA dépend des forces de deux fonctions distinctes. Le cryptosystème RSA est le plus populaire cryptosystème à clé publique dont la force est basée sur la difficulté pratique de factoriser les très grands nombres.,

• fonction de cryptage − elle est considérée comme une fonction à Sens Unique de conversion du texte brut en texte chiffré et elle ne peut être inversée qu’avec la connaissance de la clé privée D.

• génération de clé-la difficulté de déterminer une clé privée à partir d’une clé publique RSA équivaut à factoriser le module N. un attaquant ne peut donc pas utiliser la connaissance d’une clé publique RSA pour déterminer une clé privée RSA à moins qu’il ne puisse factoriser N. c’est aussi une fonction à Sens Unique, allant de p & les valeurs Q au module n sont faciles mais l’inverse n’est pas possible.,

Si l’une de ces deux fonctions est prouvée non unidirectionnelle, alors RSA sera cassé. En fait, si une technique d’affacturage efficace est développée, RSA ne sera plus sûr.

la force du chiffrement RSA diminue considérablement contre les attaques si les nombres p et q ne sont pas de grands nombres premiers et / ou si la clé publique choisie e est un petit nombre.

cryptosystème ElGamal

avec RSA, il existe d’autres cryptosystèmes à clé publique proposés. Beaucoup d’entre eux sont basés sur différentes versions du problème du logarithme discret.,

Le cryptosystème ElGamal, appelé variante de courbe elliptique, est basé sur le problème du logarithme discret. Il tire la force de l’hypothèse que les logarithmes discrets ne peuvent pas être trouvés dans un laps de temps pratique pour un nombre donné, tandis que le fonctionnement inverse de la puissance peut être calculé efficacement.

passons en revue une version simple D’ElGamal qui fonctionne avec des nombres modulo P. dans le cas des variantes de courbes elliptiques, il est basé sur des systèmes de nombres très différents. ,

génération de la paire de clés ElGamal

chaque utilisateur du cryptosystème ElGamal génère la paire de clés comme suit −

• En choisissant un grand nombre premier P. généralement, un nombre premier de 1024 à 2048 bits de longueur est choisi.

• le Choix d’un élément générateur de g.

  • Ce nombre doit être compris entre 1 et p − 1, mais ne peut pas être n’importe quel nombre.

  • c’est un générateur du groupe multiplicatif d’entiers modulo p. cela signifie que pour chaque entier m co-premier à p, Il existe un entier k tel que gk=a mod N.,

    par exemple, 3 est générateur du groupe 5 (Z5 = {1, 2, 3, 4}).

N	3n	3n mod 5
1	3	3
2	9	4
3	27	2
4	81	1

• le Choix de la clé privée. La clé privée x est un nombre plus grand que 1 et plus petit que p−1.

• calcul d’une partie de la clé publique., La valeur y est calculée à partir des paramètres p, g et la clé privée x comme suit:

y = gx mod p

• l’Obtention de la clé Publique. La clé publique ElGamal se compose des trois paramètres (p, g, y).

  par exemple, supposons que p = 17 et que g = 6 (on peut confirmer que 6 est un générateur du groupe Z17). La clé privée x peut être n’importe quel nombre supérieur à 1 et inférieur à 71, nous choisissons x = 5. La valeur y est alors calculée comme suit:

y = 65 mod 17 = 7

• Donc la clé privée est de 62 ans et la clé publique est (17, 6, 7).,

chiffrement et déchiffrement

la génération D’une paire de clés ElGamal est relativement plus simple que le processus équivalent pour RSA. Mais le cryptage et le décryptage sont légèrement plus complexes que RSA.

chiffrement ElGamal

supposons que l’expéditeur souhaite envoyer un texte en clair à quelqu’un dont la clé publique ElGamal est (p, g, y), alors −

• L’expéditeur représente le texte en clair comme une série de nombres modulo p.

• pour chiffrer le premier texte en clair P, qui, Le processus de cryptage pour obtenir le texte chiffré C est le suivant-

  • générer aléatoirement un nombre k;
  • calculer deux valeurs C1 et C2, où −

C1 = gk mod pC2 = (P*yk) mod p

• envoyer le texte chiffré C, composé des deux valeurs distinctes (C1, C2), envoyées ensemble.,

• se référant à notre exemple de génération de clé ElGamal donné ci −dessus, le texte en clair P = 13 est crypté comme suit −

  • générer aléatoirement un nombre, disons k = 10
  • calculer les deux valeurs C1 et C2, où –

C1 = 610 mod 17C2 = (13*710) mod 17 = 9

• envoyer le texte chiffré C = (C1, C2) = (15, 9).,

ElGamal Déchiffrement

• Pour déchiffrer le texte chiffré (C1, C2) à l’aide de la clé privée x, les deux étapes suivantes sont prises −

  • Calculer l’inverse modulaire de (C1)x modulo p, ce qui est (C1)-x , généralement considéré comme facteur de déchiffrement.,

  • Obtenir le texte en clair à l’aide de la formule suivante: −

C2 × (C1)-x mod p = Plaintext

• Dans notre exemple, pour déchiffrer le texte chiffré C = (C1, C2) = (15, 9) à l’aide de la clé privée x = 5, le déchiffrement facteur est

15-5 mod 17 = 9

• l’Extrait de texte clair P = (9 × 9) mod 17 = 13.

analyse ElGamal

dans le système ElGamal, chaque utilisateur a une clé privée X. et a trois composants de clé publique − premier module p, générateur g et public Y = GX mod p., La force de L’ElGamal est basée sur la difficulté du problème du logarithme discret.

la taille de clé sécurisée est généralement> 1024 bits. Aujourd’hui, même 2048 bits longue clé sont utilisés. Sur le front de la vitesse de traitement, Elgamal est assez lent, il est principalement utilisé pour les protocoles d’authentification par clé. En raison de l’efficacité de traitement plus élevée, les variantes de courbe elliptique D’ElGamal deviennent de plus en plus populaires.,

cryptographie à courbe elliptique (ECC)

La cryptographie à courbe elliptique (ECC) est un terme utilisé pour décrire une suite d’outils et de protocoles cryptographiques dont la sécurité est basée sur des versions spéciales du problème du logarithme discret. Il n’utilise pas de nombres modulo P.

ECC est basé sur des ensembles de nombres associés à des objets mathématiques appelés courbes elliptiques. Il existe des règles pour ajouter et calculer des multiples de ces nombres, tout comme il existe pour les nombres modulo p.,

ECC comprend des variantes de nombreux schémas cryptographiques initialement conçus pour des nombres modulaires tels que le cryptage ElGamal et L’algorithme de Signature numérique.

Il croit que le problème du logarithme discret est beaucoup plus difficile lorsqu’il est appliqué à des points sur une courbe elliptique. Cela invite à passer des nombres modulo p aux points d’une courbe elliptique. Un niveau de sécurité équivalent peut également être obtenu avec des clés plus courtes si nous utilisons des variantes basées sur des courbes elliptiques.,

Les clés plus courtes ont deux avantages −

• facilité de gestion des clés
• calcul efficace

ces avantages rendent les variantes de schéma de chiffrement basées sur des courbes elliptiques très attrayantes pour les applications où les ressources informatiques sont limitées.

schémas RSA et ElGamal – une comparaison

comparons brièvement les schémas RSA et ElGamal sur les différents aspects.

RSA	ElGamal
Il est plus efficace pour le chiffrement.	Il est plus efficace pour le décryptage.,
C’est moins efficace pour le décryptage.	Il est plus efficace pour le décryptage.
pour un niveau de sécurité particulier, des clés longues sont requises dans RSA.	pour le même niveau de sécurité, des clés très courtes sont requises.
Il est largement accepté et utilisé.	il est nouveau et pas très populaire sur le marché.