pour utiliser le calculateur d’angle de référence, entrez simplement n’importe quel angle dans la case angle pour trouver son angle de référence, qui est l’angle aigu qui correspond à l’angle entré. La calculatrice applique automatiquement les règles que nous examinerons ci-dessous.
qu’est Ce qu’un Angle de Référence, de toute façon?
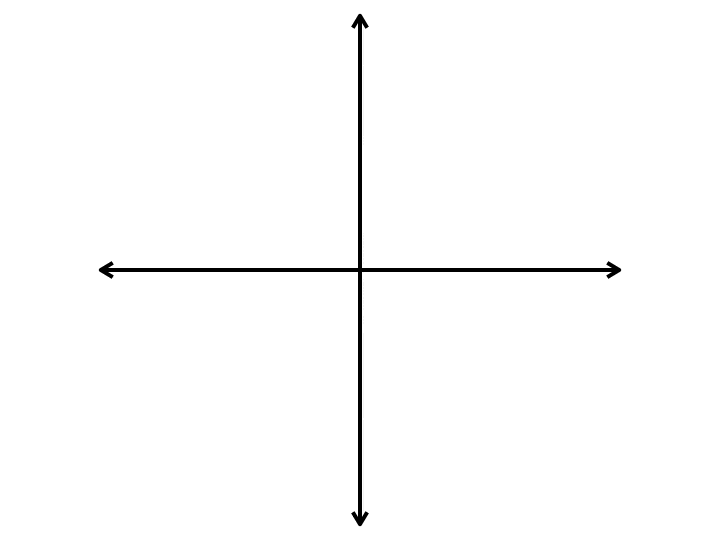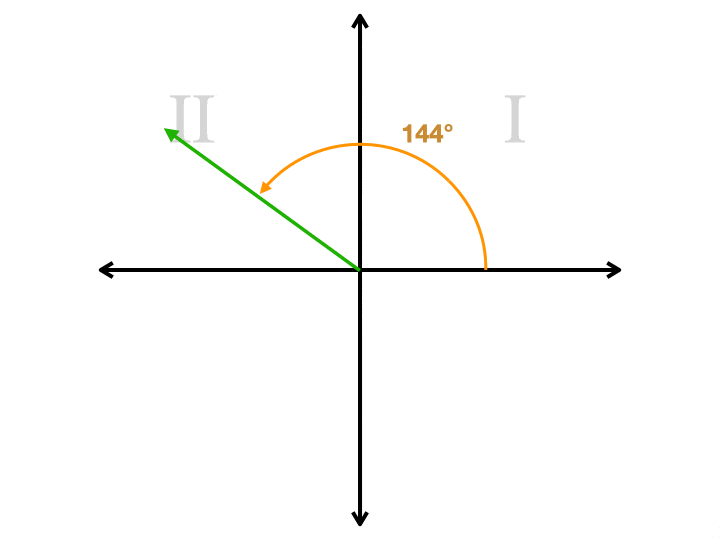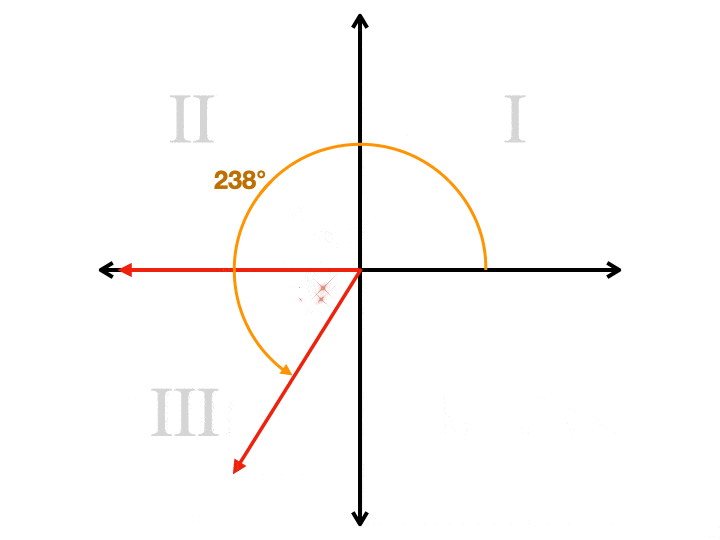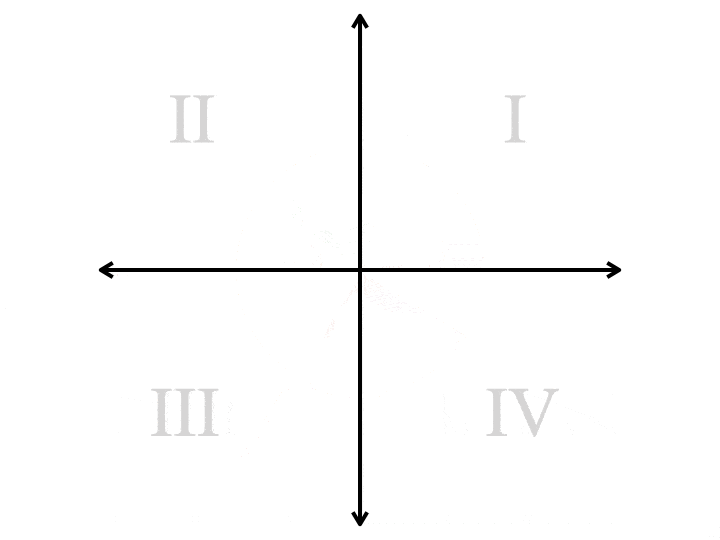
Imaginez un plan de coordonnées. Disons que nous voulons dessiner un angle de 144° sur notre plan., Nous commençons sur le côté droit de l’axe des x, où trois heures sur une horloge. Nous tournons dans le sens antihoraire, ce qui commence par monter. Nous continuons à dépasser le point de 90° (la partie supérieure de l’axe y) jusqu’à ce que nous arrivions à 144°. Nous dessinons un rayon de l’origine, qui est le centre du plan, à ce point. Maintenant, nous avons un rayon que nous appelons le côté terminal. Mais nous devons dessiner un rayon de plus pour faire un angle. Nous avons le choix à ce stade. Notre deuxième rayon doit être sur l’axe des abscisses. Si nous le dessinons de l’origine vers le côté droit, nous aurons dessiné un angle qui mesure 144°., Si nous le dessinons vers la gauche, nous aurons dessiné un angle qui mesure 36°. Ce deuxième angle est l’angle de référence. C’est toujours la plus petite des deux angles, sera toujours inférieur ou égal à 90°, et il sera toujours positif. Voici une animation qui montre un angle de référence pour quatre angles différents, dont chacun est dans un quadrant différent. Remarquez comment le deuxième rayon est toujours sur l’axe des abscisses.
Comment est l’Angle de Référence Utile?
l’angle de référence a toujours les mêmes valeurs de fonction trig que l’angle d’origine. Notez les valeurs de mot là., Le signe peut ne pas être le même, mais la valeur sera toujours. Ceci est utile pour les angles communs comme 45° et 60° que nous rencontrerons encore et encore. Une fois que nous connaissons leurs valeurs sinus, cosinus et tangentes, nous connaissons également les valeurs pour tout angle dont l’angle de référence est également de 45° ou 60°. En ce qui concerne le signe, rappelez-vous que le sinus est positif dans le 1er et le 2ème quadrant et que le cosinus est positif dans le 1er et le 4ème quadrant.
Comment Trouver l’Angle de Référence sans Calculatrice?
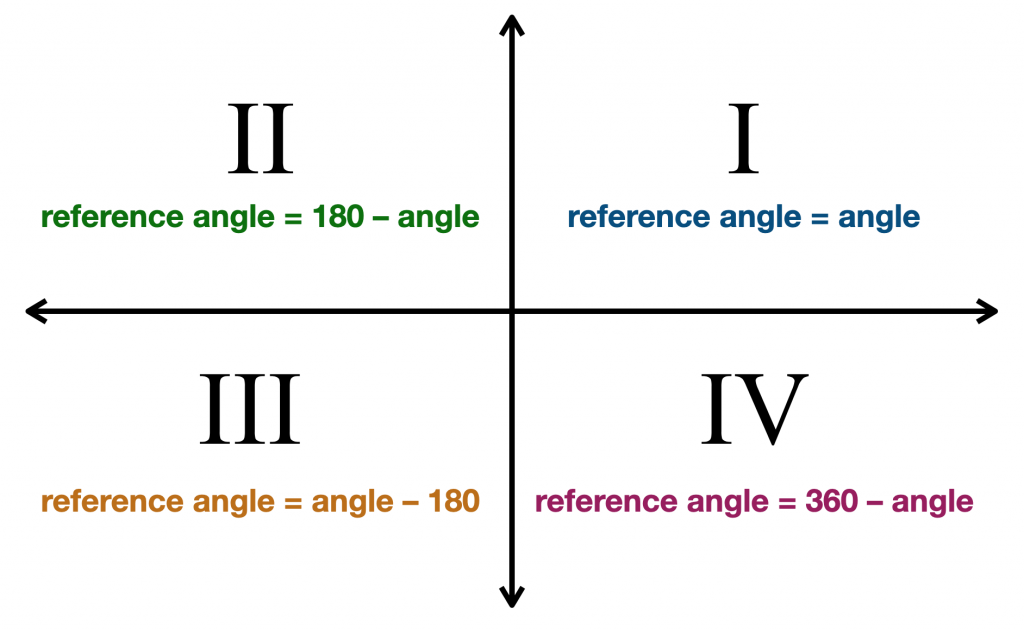
la façon dont nous trouvons l’angle de référence dépend du quadrant du côté terminal.,
Lorsque le côté terminal est dans le premier quadrant (angles de 0° à 90°), notre angle de référence est le même que notre angle donné. Cela a du sens, car tous les angles du premier quadrant sont inférieurs à 90°. Donc, si notre angle donné est 33°, alors son angle de référence est également 33°.
lorsque le côté terminal est dans le deuxième quadrant (angles de 90° à 180°), notre angle de référence est de 180° moins notre angle donné. Donc, si notre angle donné est 110°, alors son angle de référence est 180° – 110° = 70°.,
Lorsque le côté terminal est dans le troisième quadrant (angles de 180° à 270°), notre angle de référence est notre angle donné moins de 180°. Donc, si notre angle donné est 214°, alors son angle de référence est 214° – 180° = 34°.
Lorsque le côté terminal est dans le quatrième quadrant (angles de 270° à 360°), référence de l’angle est de 360°, moins notre angle donné. Donc, si notre angle donné est 332°, alors son angle de référence est 360° – 332° = 28°.
Que faire si Notre Angle est Supérieur à 360°?,
lorsqu’un angle est supérieur à 360°, cela signifie qu’il a tourné tout autour du plan de coordonnées et a continué. Afin de trouver son angle de référence, nous devons d’abord trouver son angle correspondant entre 0° et 360°. C’est facile à faire. Nous continuons à en soustraire 360 jusqu’à ce qu’il soit inférieur à 360. Par exemple, si notre angle est de 544°, nous soustraire à 360° pour 184° (544° – 360° = 184°). Maintenant, nous remarquerions que c’est dans le troisième quadrant, donc nous en soustrayerions 180° pour trouver que notre angle de référence est 4°.
et si notre Angle est négatif?,
Lorsqu’un angle est négatif, nous passons l’autre sens pour trouver notre côté terminal. Cela signifie que nous nous déplaçons dans le sens horaire au lieu du sens antihoraire lors du dessin. Ou nous pouvons le calculer en l’ajoutant simplement à 360°. Par exemple, si notre angle donné est -110°, alors nous l’ajouterions à 360° pour trouver notre angle positif de 250° (-110° + 360° = 250°). Maintenant, nous devons voir que nous sommes dans le troisième quadrant, et appliquer cette règle pour trouver notre angle de référence (250° – 180° = 70°).